Stata에서 kruskal-wallis 테스트를 수행하는 방법

Kruskal-Wallis 검정은 세 개 이상의 독립 그룹의 중앙값 간에 통계적으로 유의미한 차이가 있는지 여부를 확인하는 데 사용됩니다. 이는 일원 분산 분석 과 동등한 비모수적 분석으로 간주됩니다.

이 튜토리얼에서는 Stata에서 Kruskal-Wallis 테스트를 수행하는 방법을 설명합니다.

Stata에서 Kruskal-Wallis 테스트를 수행하는 방법

이 예에서는 미국 50개 주 전체에 대한 1980년 인구 조사 데이터가 포함된 인구 조사 데이터 세트를 사용합니다. 데이터 세트에서 주는 네 가지 지역으로 분류됩니다.

• 노르드에스트
• 노스 센트럴
• 남쪽
• 서쪽

우리는 Kruskal-Wallis 테스트를 수행하여 이 4개 지역의 평균 연령이 동일한지 확인합니다.

1단계: 데이터를 로드하고 표시합니다.

먼저 명령 상자에 다음 명령을 입력하여 데이터세트를 로드합니다.

https://www.stata-press.com/data/r13/census를 사용하세요.

다음 명령을 사용하여 데이터세트에 대한 빠른 요약을 가져옵니다.

요약

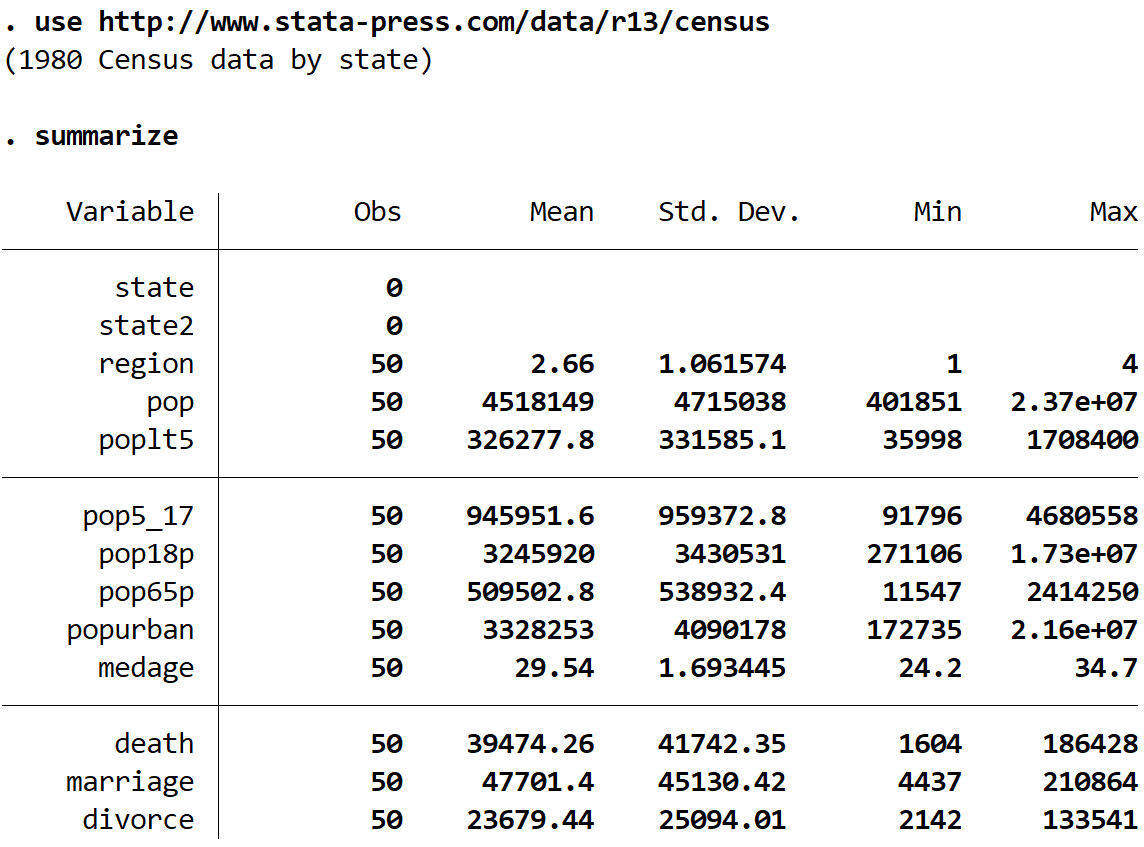
이 데이터세트에는 13개의 서로 다른 변수가 있음을 알 수 있지만 우리가 작업할 변수는 medage (중간 연령)와 지역 뿐입니다.

2단계: 데이터를 시각화합니다.

Kruskal-Wallis 테스트를 수행하기 전에 먼저 네 지역 각각의 평균 연령 분포를 시각화하기 위해 몇 가지 상자 그림을 만들어 보겠습니다 .

메디지 그래픽 상자, 켜짐(지역)

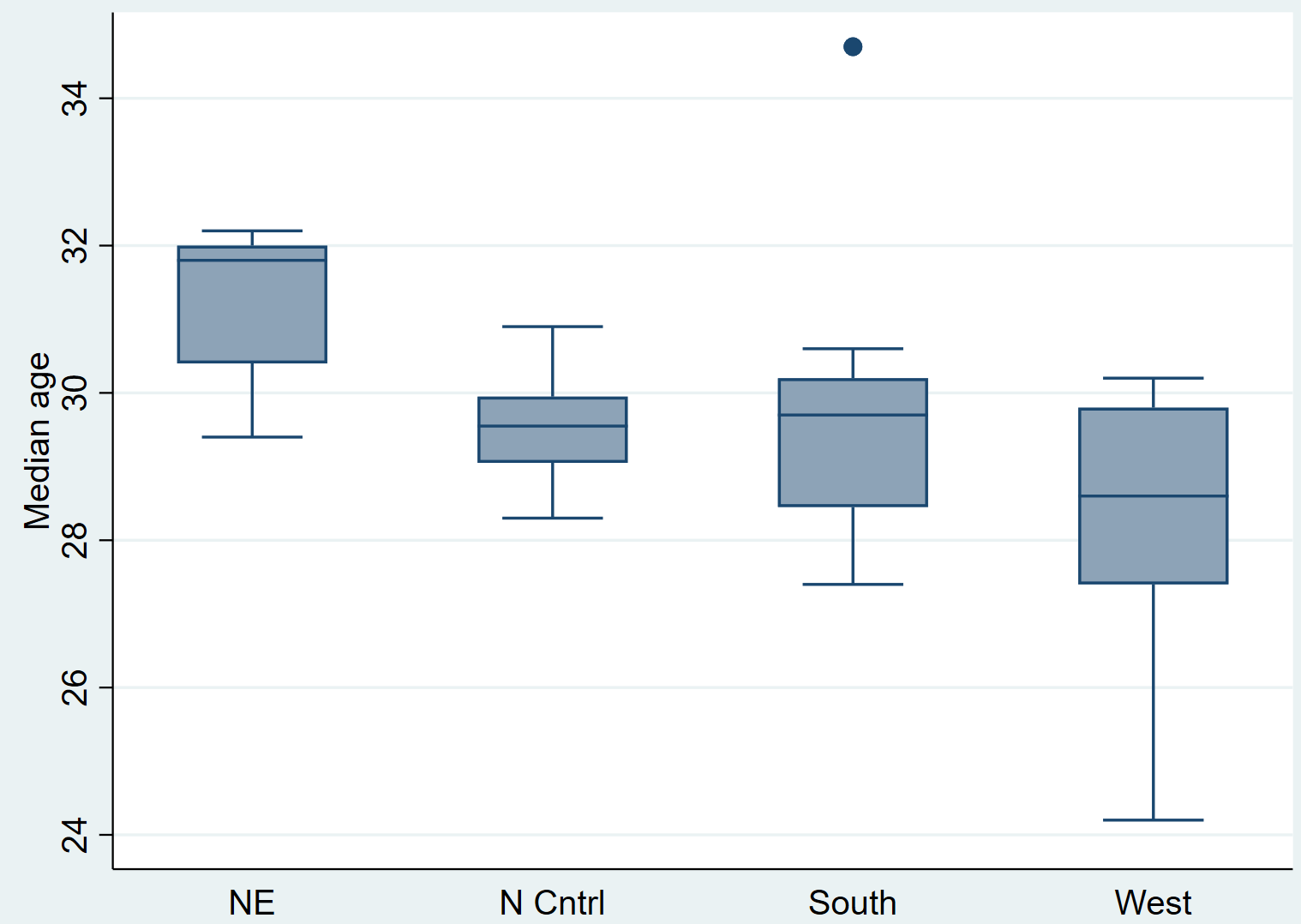
상자 그림을 보면 분포가 지역마다 다른 것처럼 보이는 것을 알 수 있습니다. 그런 다음 Kruskal-Wallis 테스트를 수행하여 이러한 차이가 통계적으로 유의한지 확인합니다.

3단계: Kruskal-Wallis 테스트를 수행합니다.

Kruskal-Wallis 테스트를 수행하려면 다음 구문을 사용하십시오.

kwallis 측정_변수, 기준(그룹화_변수)

이 경우에는 다음 구문을 사용합니다.

Kwallis medage, 작성자: (지역)

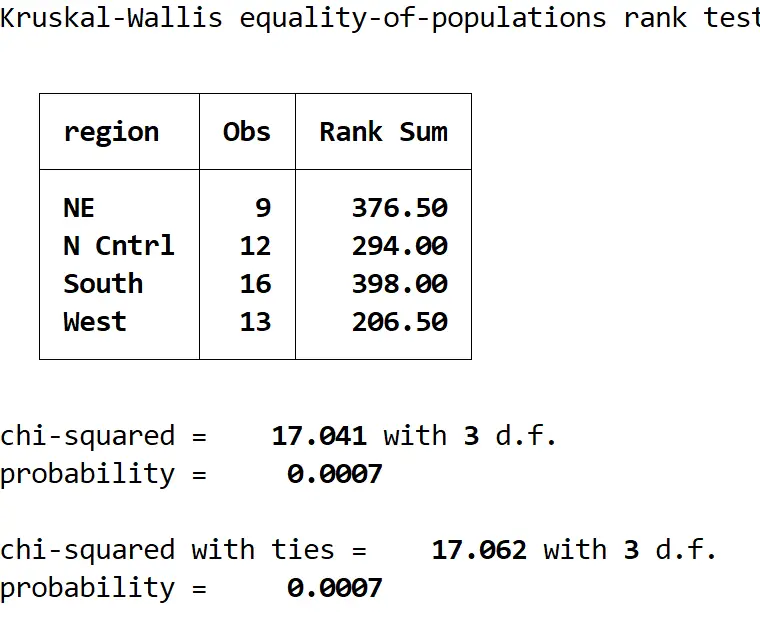
결과를 해석하는 방법은 다음과 같습니다.

요약표: 이 표에는 지역별 관측치 수와 지역별 순위 합계가 표시됩니다.

동점이 있는 카이제곱: 검정 통계량의 값으로 17.062로 나타납니다.

확률: 검정 통계량에 해당하는 p-값으로 0.0007로 나타납니다. 이 값은 0.05보다 작으므로 귀무가설을 기각하고 네 지역의 중위연령이 동일하지 않다는 결론을 내릴 수 있습니다.

4단계: 결과를 보고합니다.

마지막으로 Kruskal-Wallis 테스트 결과를 보고하고자 합니다. 이를 수행하는 방법의 예는 다음과 같습니다.

Kruskal-Wallist 테스트는 미국의 다음 4개 지역에서 개인의 평균 연령이 동일한지 확인하기 위해 수행되었습니다.

• 북동부(n=9)
• 북중부(n=12)
• 남쪽(n=16)
• 서부(n=13)

테스트 결과, 4개 지역에서 개인의 평균 연령이 동일하지 않은 것으로 나타났습니다(X ² = 17.062, p = 0.0007). 즉, 두 개 이상의 지역 간 중위연령에 통계적으로 유의미한 차이가 있었습니다.