평균 차이의 샘플링 분포

에 의해 벤자민 앤더슨 8월 3, 2023 통계 댓글 0개

이 기사에서는 통계에서 두 평균 간의 차이에 대한 샘플링 분포가 무엇인지 설명합니다. 또한 평균 차이의 샘플링 분포에 대한 공식과 단계별 해결 연습도 확인할 수 있습니다.

평균 차이의 표본 분포는 무엇입니까?

평균 차이의 표본 분포는 서로 다른 두 모집단의 가능한 모든 표본 평균 간의 차이를 계산하여 얻은 분포입니다.

즉, 평균 차이의 표본분포를 얻기 위해서는 두 모집단에서 가능한 모든 표본을 선택하고, 선택된 각 표본의 평균을 계산하고, 마지막으로 두 모집단에서 계산된 모든 평균의 차이를 구해야 한다. 따라서 이러한 모든 작업을 적용한 후에 얻은 값 집합은 평균 차이의 샘플링 분포를 형성합니다.

평균 표본 추출 분포의 차이는 서로 다른 두 모집단에서 임의로 선택한 표본의 두 평균 간의 차이가 모집단 평균의 차이에 가까울 확률을 계산하는 데 사용됩니다.

➤ 참조: 평균의 표본 분포

평균 차이의 표본 분포 공식

표본 크기가 충분히 큰 경우(n ₁ ≥30 및 n ₂ ≥30) 평균 차이의 표본 추출 분포는 정규 분포를 따릅니다. 보다 정확하게는 상기 분포의 매개변수는 다음과 같이 계산됩니다.

$\begin{array}{c}\displaystyle \mu_{\overline{x_1}-\overline{x_2}}=\mu_1-\mu_2 \qquad \sigma_{\overline{x_1}-\overline{x_2}}=\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\\[6ex]\displaystyle N_{\overline{x_1}-\overline{x_2}}\left(\mu_1-\mu_2, \sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right) \end{array}$

참고: 두 모집단이 모두 정규 분포 인 경우 평균 차이의 샘플링 분포는 표본 크기에 관계없이 정규 분포를 따릅니다.

따라서 평균차의 표본분포는 정규분포로 정의되므로 평균차 의 표본분포 통계량을 계산하는 공식은 다음과 같습니다.

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}}$

금:

$\overline{x_i}$

표본 i의 평균입니다.
$\mu_i$

는 인구 i의 평균이다.
$\sigma_i$

는 모집단 i의 표준편차입니다.
$n_i$

표본 크기는 i입니다.
$Z$

는 표준 정규 분포 N(0,1)에 의해 정의되는 변수입니다.

다양한 모집단의 표본은 표본 크기가 다를 수 있습니다.

평균차의 표본분포의 구체적인 예

평균 표본 추출 분포의 차이에 대한 정의와 그 공식이 무엇인지 살펴보고 나면, 단계별 예제를 통해 평균 표본 추출 분포의 차이에 대한 개념 이해를 마무리하겠습니다.

통계 연구에서는 특정 연령의 남자아이와 여자아이의 키 차이를 분석하고 싶습니다. 우리는 이 연령대의 남아 인구를 정의하는 분포의 평균이 157cm, 표준편차가 9cm인 반면, 이 연령대의 여학생 인구를 정의하는 분포의 평균은 148cm라는 것을 알고 있습니다. cm이고 표준편차는 7cm입니다. 이 연령의 남아 30명의 표본과 이 연령의 여아 35명의 표본을 선택한 경우, 남아 표본의 평균 키가 여아 표본의 평균 키보다 12cm 더 클 확률은 얼마입니까?

이 문제를 해결하기 위해 가장 먼저 해야 할 일은 평균표본분포의 차이에 대한 통계량을 계산하는 것이다. 따라서 위에서 본 공식을 적용합니다.

$Z=\cfrac{(\overline{x_1}-\overline{x_2})-(\mu_1-\mu_2)}{\displaystyle\sqrt{\frac{\sigma_1^2}{n_1}+\frac{\sigma_2^2}{n_2}}\right)}=\cfrac{12-(157-148)}{\displaystyle\sqrt{\frac{9^2}{30}+\frac{7^2}{35}}}=1,48$

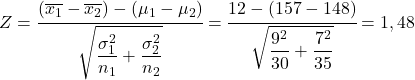
따라서 남자아이의 평균 표본 키가 여자아이의 평균 키보다 12cm 더 클 확률은 Z 변수가 1.48보다 클 확률과 동일합니다.

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]” title=”Rendered by QuickLaTeX.com” height=”19″ width=”253″ style=”vertical-align: -5px;”></p> </p> <p> 따라서 우리는 <a href=$ Z 테이블 에서 Z>1.48의 확률을 찾습니다.

$P[(\overline{x_1}-\overline{x_2})>12]=P[Z>1,48]=0,0694″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”331″ style=”vertical-align: -5px;”></p> </p> <p> 즉, 남자아이의 평균 표본키가 여자아이의 평균키보다 12cm 더 클 확률은 6.94%이다.</p> </div>  <div class=$

저자 소개

벤자민 앤더슨

안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기

평균 차이의 표본 분포는 무엇입니까?

평균 차이의 표본 분포 공식

평균차의 표본분포의 구체적인 예

저자 소개

벤자민 앤더슨

의견을 추가하다