Stata에서 2차 회귀를 수행하는 방법

두 변수가 선형 관계를 갖는 경우 단순 선형 회귀 분석을 사용하여 관계를 정량화할 수 있는 경우가 많습니다.

그러나 두 변수가 2차 관계를 갖는 경우 2차 회귀 분석을 사용하여 해당 관계를 수량화할 수 있습니다.

이 튜토리얼에서는 Stata에서 2차 회귀를 수행하는 방법을 설명합니다.

예: Stata의 2차 회귀

우리가 근무 시간과 행복 사이의 관계를 이해하고 싶다고 가정해 보겠습니다. 우리는 16명의 서로 다른 사람들에 대한 주당 근무 시간과 보고된 행복 수준(0~100점)에 대한 다음과 같은 데이터를 가지고 있습니다.

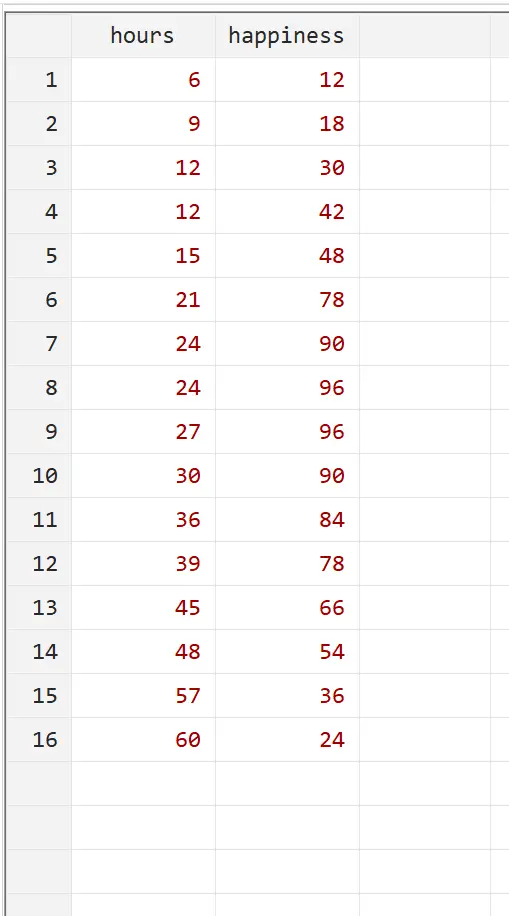
상단 메뉴의 데이터 > 데이터 편집기 > 데이터 편집기(편집)를 사용하여 Stata에 정확한 데이터를 입력하면 이 예제를 재현할 수 있습니다.

Stata에서 2차 회귀를 수행하려면 다음 단계를 따르세요.

1단계: 데이터를 시각화합니다.

2차 회귀를 사용하려면 먼저 설명 변수(시간)와 응답 변수(행복) 간의 관계가 실제로 2차인지 확인해야 합니다. 이제 명령 상자에 다음을 입력하여 산점도를 사용하여 데이터를 시각화해 보겠습니다 .

행복한 시간을 분산시키다

그러면 다음과 같은 산점도가 생성됩니다.

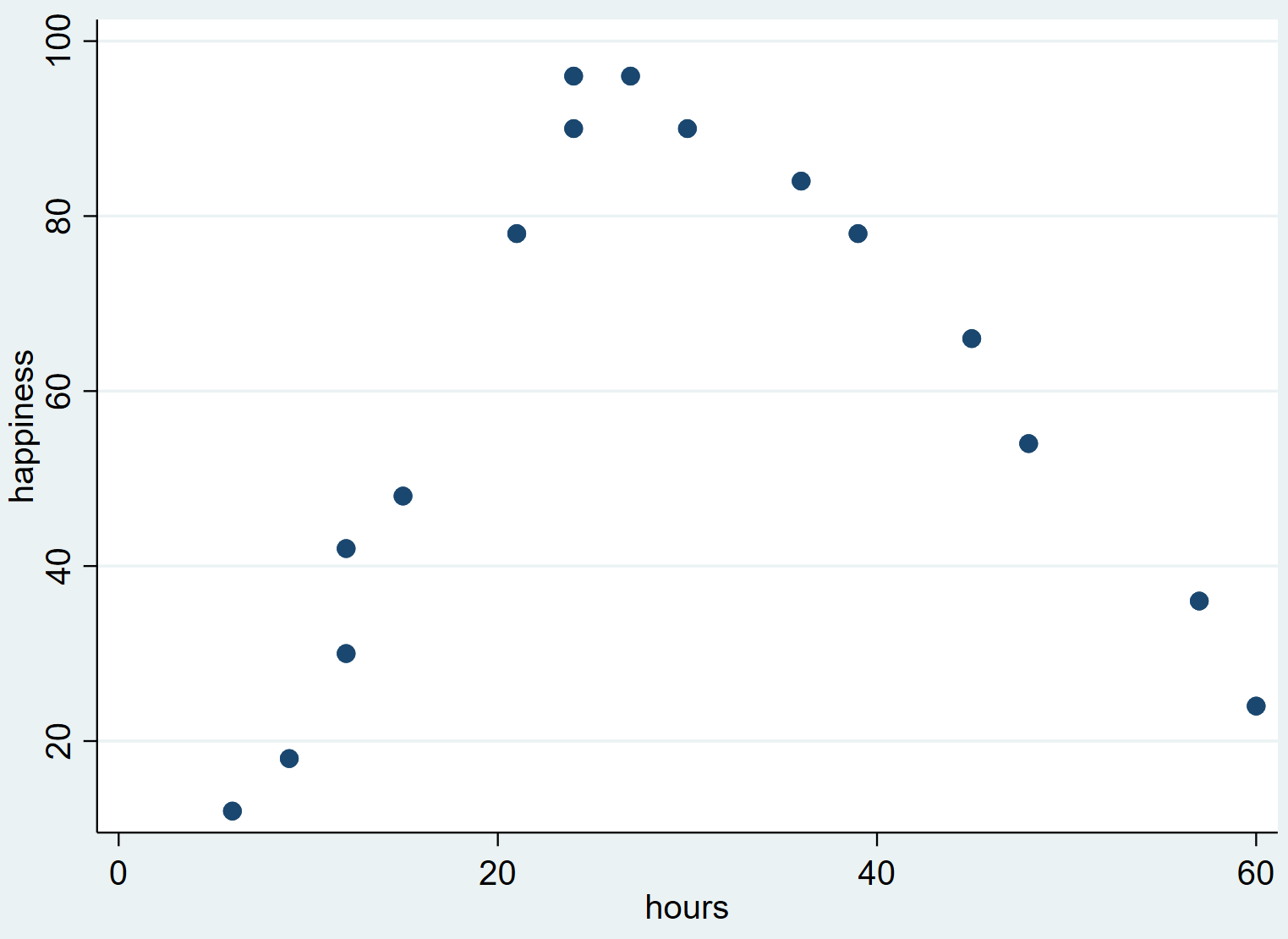
행복도는 근무시간이 0시간에서 일정 지점까지 증가할수록 높아지다가, 근무시간이 30시간을 넘으면 감소하기 시작하는 경향이 있음을 알 수 있습니다.

산점도의 반전된 “U” 모양은 근무 시간과 행복 사이에 2차 관계가 있음을 나타냅니다. 이는 이 관계를 정량화하기 위해 2차 회귀를 사용해야 함을 의미합니다.

2단계: 2차 회귀를 수행합니다.

2차 회귀 모델을 데이터에 맞추기 전에 시간 예측 변수의 제곱 값에 대한 새 변수를 만들어야 합니다. 명령 상자에 다음을 입력하면 됩니다.

세대 시간2 = 시간*시간

상단 메뉴에서 데이터 > 데이터 편집기 > 데이터 편집기(찾아보기) 로 이동하여 이 새 변수를 볼 수 있습니다.

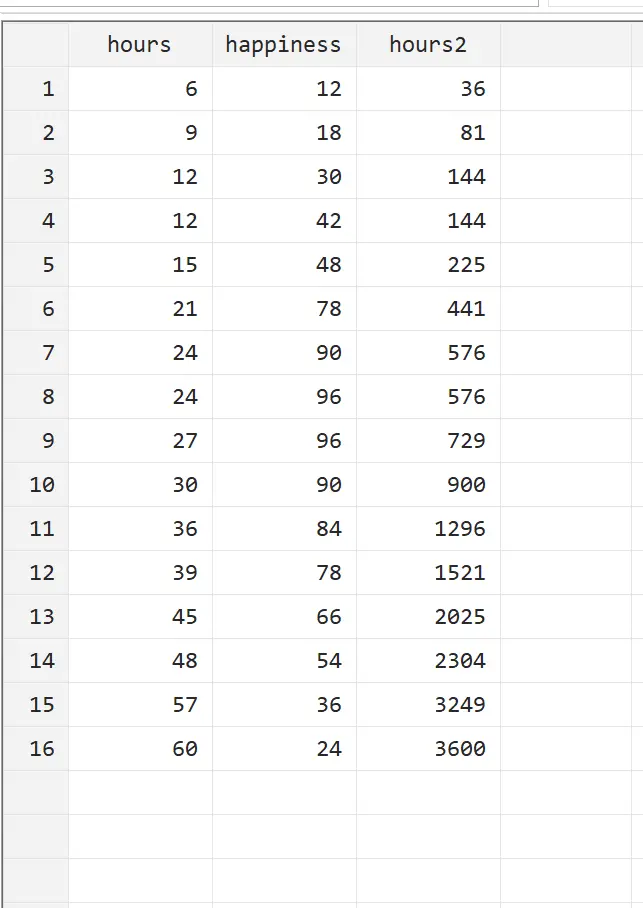
hour2는 단순히 시간의 제곱임을 알 수 있습니다. 이제 설명 변수로 hour 와 hour2를 사용하고 반응 변수로 행복을 사용하여 2차 회귀를 수행할 수 있습니다. 2차 회귀를 수행하려면 명령 상자에 다음을 입력하십시오.

회귀 시간의 행복 시간2

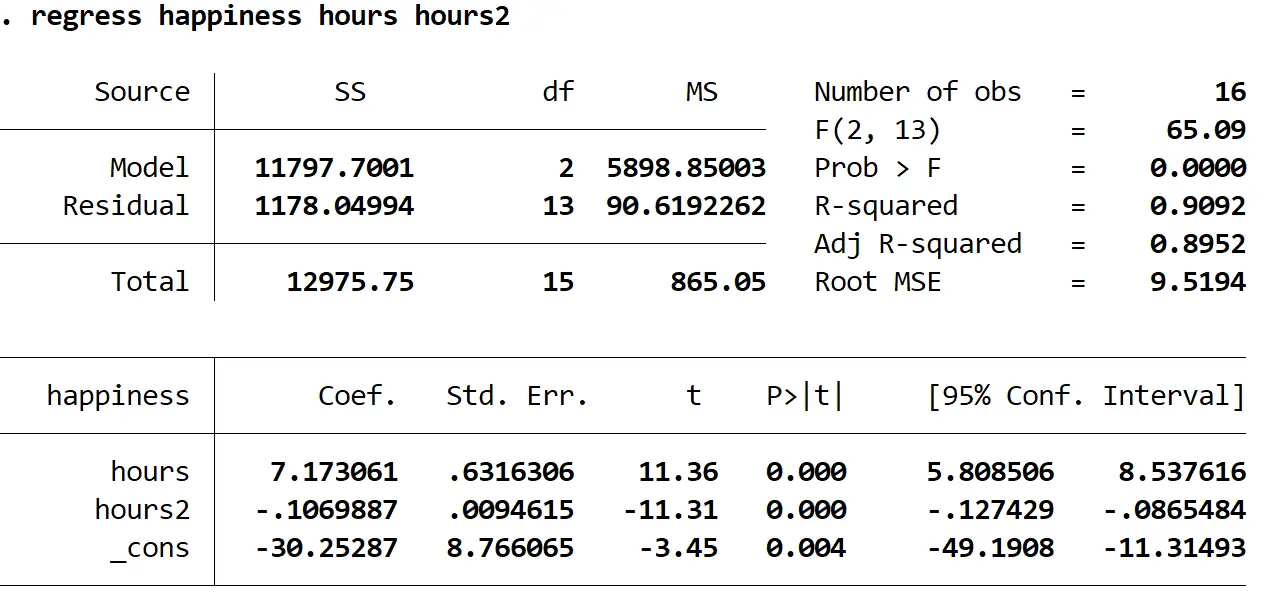
결과에서 가장 흥미로운 숫자를 해석하는 방법은 다음과 같습니다.

확률 > F: 0.000. 이는 전체 회귀에 대한 p-값입니다. 이 값이 0.05보다 작기 때문에 이는 예측 변수 시간 과 시간 ^2를 합친 것이 반응 변수 행복 과 통계적으로 유의미한 관계를 가지고 있음을 의미합니다.

R 제곱: 0.9092. 이는 설명 변수로 설명할 수 있는 반응 변수의 분산 비율입니다. 이 예에서는 행복 변화의 90.92%가 시간 과 시간으로 설명될 수 있습니다 ² .

회귀 방정식: 출력 테이블에 표시된 계수 값을 사용하여 회귀 방정식을 구성할 수 있습니다. 이 경우 방정식은 다음과 같습니다.

예상 행복 = -30.25287 + 7.173061(시간) – 0.1069887( ² 시간)

우리는 이 방정식을 사용하여 개인의 주당 근무 시간을 바탕으로 개인의 예상 행복을 찾을 수 있습니다.

예를 들어, 주당 60시간 일하는 사람의 행복 수준은 14.97이어야 합니다.

예상 행복 = -30.25287 + 7.173061(60) – .1069887(60 ² ) = 14.97 .

반대로, 주당 30시간 일하는 사람의 행복 수준은 88.65입니다.

예상 행복 = -30.25287 + 7.173061(30) – .1069887(30 ² ) = 88.65 .

3단계: 결과를 보고합니다.

마지막으로 2차 회귀 분석 결과를 보고하려고 합니다. 이를 수행하는 방법의 예는 다음과 같습니다.

개인이 근무한 시간과 해당 행복 수준(0에서 100까지 측정) 사이의 관계를 정량화하기 위해 2차 회귀 분석을 수행했습니다. 분석에는 16명의 표본이 사용되었습니다.

결과는 설명 변수인 시간 과 시간 ² 와 반응 변수 행복 사이에 통계적으로 유의한 관계가 있음을 보여주었습니다(F(2, 13) = 65.09, p < 0.0001).

이 두 가지 설명 변수는 설명된 행복 변동성의 90.92%를 설명했습니다.

회귀 방정식은 다음과 같습니다.

예상 행복 = -30.25287 + 7.173061(시간) – 0.1069887( ² 시간)