5분위수(통계)

이 글에서는 5분위수가 무엇이고 어떻게 계산되는지 설명합니다. 5분위수 계산에 대한 몇 가지 해결된 예를 찾을 수 있으며, 또한 온라인 계산기를 사용하여 통계 표본의 5분위수를 계산할 수 있습니다.

5분위수란 무엇입니까?

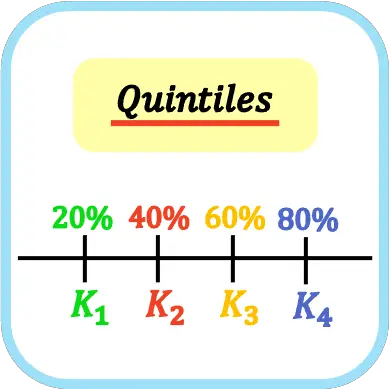
통계에서 5분위수는 데이터 세트를 5개의 동일한 부분으로 나누는 4개의 값입니다. 따라서 첫 번째, 두 번째, 세 번째 및 네 번째 5분위수는 각각 표본 데이터의 20%, 40%, 60% 및 80%를 나타냅니다.

즉, 예를 들어 3분위의 값은 수집된 전체 데이터의 60%보다 높지만 나머지 데이터보다 낮습니다.

5분위수 기호는 5분위수 지수가 있는 대문자 K입니다. 즉, 첫 번째 5분위수는 K ₁ , 두 번째 5분위수는 K ₂ , 세 번째 5분위수는 K ₃ , 네 번째 5분위수는 K ₄ 입니다. 문자 Q로 표시할 수도 있지만(4분위수와 혼동을 일으키므로 권장되지 않음)

👉 아래 계산기를 사용하여 모든 데이터 세트의 5분위수를 계산할 수 있습니다.

5분위수는 4분위수, 10분위수, 백분위수와 함께 비중심 위치를 측정한 것입니다. 더 관심이 있으시면 당사 웹사이트에서 이러한 각 분위수 유형이 무엇을 의미하는지 확인할 수 있습니다.

5분위수에는 또 다른 정의가 있을 수 있다는 점에 유의해야 합니다. 경제학에서 5분위수는 소득에 따라 정렬된 인구의 비율을 나타냅니다. 즉, 소득 수준에 따라 인구의 순위를 매깁니다. 예를 들어, 첫 번째 5분위는 인구 중 가장 빈곤한 20%에 해당하고, 두 번째 5분위는 소득이 가장 낮은 인구 40%에 해당합니다.

5분위수를 계산하는 방법

표본 또는 통계 모집단의 5분위 위치를 계산 하려면 5분위 수에 전체 데이터 수의 합에 1을 더한 값을 곱하고 그 결과를 5로 나누어야 합니다.

따라서 5분위수의 공식은 다음과 같습니다.

참고: 이 공식의 결과는 5분위수의 값이 아닌 위치를 알려줍니다. 따라서 5분위수는 공식으로 얻은 위치에 있는 데이터가 됩니다.

그러나 때로는 이 공식의 결과가 십진수를 제공하므로 결과가 십진수인지 아닌지에 따라 두 가지 경우를 구별해야 합니다.

• 수식의 결과가 소수점 이하의 숫자 인 경우, 5분위수는 위 수식에서 제공하는 위치에 위치한 데이터가 됩니다.
• 수식 결과가 소수 부분이 있는 숫자 인 경우 5분위수 값은 다음 표현식을 사용하여 계산됩니다.

여기서 x _i 와 x _i+1 은 첫 번째 수식에서 구한 숫자가 위치한 위치의 숫자이고, d 는 첫 번째 수식에서 구한 숫자의 소수 부분입니다.

데이터 세트의 5분위수를 결정하는 데 너무 많은 단계를 보고 겁이 났더라도 걱정하지 마세요. 실제로는 매우 간단합니다. 다음 두 가지 예를 읽으면 훨씬 더 잘 이해하게 될 것입니다.

참고 : 통계 커뮤니티에서는 여전히 5분위수 계산 방법에 대해 완전히 동의하지 않으므로 이를 조금 다르게 설명하는 책을 찾을 수 있습니다.

5분위수 계산의 예

아래에서는 데이터 시리즈에서 5분위수를 얻는 방법에 대해 단계별로 해결되는 두 가지 연습을 남겨드립니다. 따라서 가능한 두 가지 경우를 볼 수 있습니다. 첫 번째 연습에서는 결과가 소수가 아니고 두 번째 연습에서는 결과가 소수입니다.

실시예 1

• 다음 데이터 계열의 5분위수를 계산합니다.

위의 설명에서 보았듯이 5분위수 위치를 구하는 공식은 다음과 같습니다.

매개변수 n은 총 데이터 수(49)를 나타내므로 첫 번째 5분위수의 위치를 찾으려면 n을 49로, k를 1로 바꿔야 합니다.

공식에서 우리는 숫자 10을 얻었습니다. 이는 5분위수가 정렬된 목록의 10번째 위치에 있고 데이터 205에 해당한다는 것을 의미합니다.

두 번째 5분위수를 계산하려면 동일한 공식을 사용해야 하지만 k를 2로 바꿔야 합니다.

따라서 두 번째 5분위수는 순서 목록의 위치 번호 20, 즉 값 236에 있습니다.

다시, 우리는 5분위수를 결정하는 프로세스를 반복하지만 논리적으로 이제 k를 3으로 대체합니다.

따라서 3분위수는 30위에 위치한 데이터로, 266에 해당합니다.

마지막으로 공식을 다시 적용하여 4분위수를 계산합니다.

따라서 4분위수는 40위이므로 4분위수는 286위입니다.

실시예 2

• 다음 표에 수집된 통계 데이터의 4분위수를 계산합니다.

이전 예와 같은 방식으로 5분위수 위치를 얻으려면 다음 공식을 사용해야 합니다.

이 경우 표본 크기는 42개의 관측치이므로 첫 번째 5분위수의 위치를 찾으려면 매개변수 n을 42로, k를 1로 바꿔야 합니다.

그러나 첫 번째 예와 달리 이번에는 공식이 십진수를 제공하므로 정확한 5분위수를 계산하려면 다음 공식을 적용해야 합니다.

첫 번째 공식에서 얻은 숫자는 8.6이므로 첫 번째 5분위수는 8번째와 9번째 데이터 사이에 있으며 각각 78과 79입니다. 따라서 x _i 는 78, x _i+1 은 79, d 는 얻은 숫자의 소수 부분, 즉 0.6입니다.

이제 두 번째 5분위수를 찾기 위해 똑같은 절차를 다시 수행합니다. 먼저 위치를 계산합니다.

그러나 공식에서 우리는 17에서 18 사이의 십진수를 얻습니다. 따라서 두 번째 5분위수는 17위와 18위 사이에 위치하며 그 값은 각각 순서 목록의 109와 112에 해당합니다. 따라서 정확한 5분위수 값을 결정하기 위해 프로세스에서 두 번째 공식을 적용합니다.

세 번째 5분위수를 얻기 위해 이 방법을 반복하고 먼저 위치를 결정합니다.

계산된 숫자 25.8은 5분위수 값이 25번째와 26번째 위치 사이에 있으며 그 값은 134와 141임을 의미합니다. 따라서 정확한 5분위수 값 계산은 다음과 같습니다.

마지막으로 4분위수를 계산하기 위해 마지막으로 동일한 절차를 반복합니다. 먼저 해당 위치를 찾습니다.

따라서 4분위의 정확한 값은 34와 35 사이가 되며, 그 위치는 데이터 172와 179에 해당합니다. 따라서 4분위의 계산은 다음과 같습니다.

5분위수 계산기

5분위수를 계산하려면 다음 계산기에 통계 데이터 세트를 입력하세요. 데이터는 공백으로 구분해야 하며 소수점 구분 기호로 마침표를 사용하여 입력해야 합니다.

그룹화된 데이터의 5분위수

데이터가 구간으로 그룹화될 때 5분위수를 계산 하려면 먼저 다음 공식을 사용하여 해당 구간이나 클래스를 찾아야 합니다.

따라서 5분위수는 절대 빈도가 이전 표현식으로 얻은 숫자보다 바로 큰 간격에 있게 됩니다.

그리고 5분위수가 속하는 간격을 알고 나면 다음 공식을 적용하여 5분위수의 정확한 값을 찾아야 합니다.

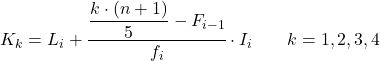
금:

• Li _는 5분위수가 위치하는 간격의 하한이다.
• n 은 총 관측치 수입니다.
• F _i-1 은 이전 구간의 누적 절대 빈도입니다.
• f _i 는 5분위수가 위치한 간격의 절대 빈도입니다.
• I _i 는 5분위 간격의 너비입니다.

이것이 어떻게 수행되는지 볼 수 있습니다. 다음은 간격으로 그룹화된 다음 데이터 계열의 5분위수를 계산하는 해결된 예입니다.

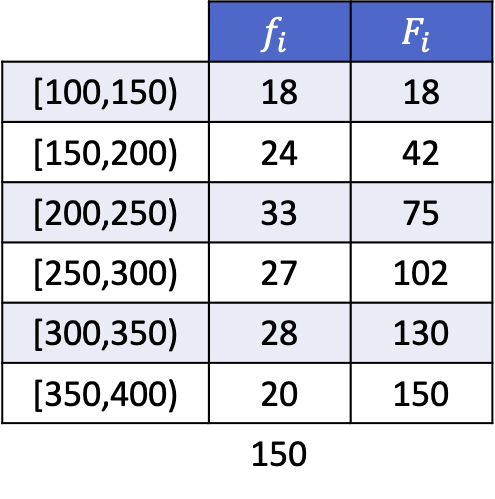
데이터가 그룹화되어 있으므로 5분위수를 계산하려면 다음 방법을 사용해야 합니다. 먼저 5분위수가 속하는 범위를 결정한 다음 5분위수의 정확한 값을 찾습니다.

따라서 첫 번째 5분위수가 위치한 간격을 찾으려면 다음 공식을 사용합니다.

첫 번째 5분위수는 누적 절대 빈도가 30.2보다 바로 큰 간격에 속하며, 이 경우 누적 절대 빈도가 42인 간격 [150,200)입니다. 그리고 5분위 간격을 알고 나면 다음의 두 번째 공식을 적용합니다. 정확한 값을 결정하는 프로세스:

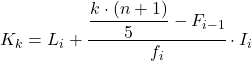
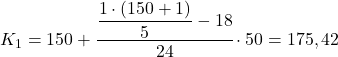
이제 두 번째 5분위수를 얻기 위해 동일한 절차를 반복하고, 먼저 그것이 있는 간격을 계산합니다.

60.4 바로 위의 누적 절대 빈도는 75이므로 두 번째 5분위 범위는 [200 250)입니다. 따라서 해당 값을 두 번째 공식에 대체하여 정확한 5분위수 값을 계산합니다.

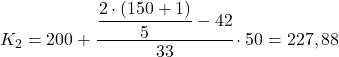
3분위수를 얻기 위해 동일한 절차를 세 번째로 수행합니다. 먼저 5분위수가 위치하는 간격을 결정합니다.

5분위수는 누적 절대 빈도(102)가 90.6 바로 위에 있기 때문에 간격 [250,300)에 있습니다. 따라서 세 번째 5분위수의 정확한 값은 다음과 같이 계산됩니다.

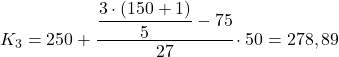
마지막으로 4분위수를 찾아보겠습니다. 항상 그렇듯이 먼저 간격을 찾습니다.

절대 빈도가 120.8보다 바로 큰 간격은 [300.350)이고 값은 130입니다. 따라서 4분위수의 정확한 값은 다음과 같습니다.