분산에 대한 가설 검정

에 의해 벤자민 앤더슨 8월 3, 2023 통계 댓글 0개

이 문서에서는 분산에 대한 가설 검정이 무엇인지 설명합니다. 따라서 분산 가설 검정을 위한 공식과 더불어 단계별로 해결되는 연습 문제도 찾을 수 있습니다.

분산에 대한 가설 검정이란 무엇입니까?

분산 가설 검정은 모집단 분산의 귀무 가설을 기각할지 여부를 결정하는 데 사용되는 통계적 방법입니다. 즉, 분산 가설 검정은 모집단의 분산 값에 대한 가설을 기각하거나 수락하는 데 사용됩니다.

특히, 분산에 대한 가설 검정 통계 값과 선택한 유의 수준에 따라 귀무 가설이 기각되거나 채택됩니다.

가설 검정은 다양한 이름으로 불리며 가설 대조, 가설 검정 또는 유의성 검정이라고도 합니다.

분산에 대한 가설 검정 공식

분산에 대한 가설 검정 통계량은 표본 크기에서 표본 분산의 1배를 뺀 값을 제안된 모집단 분산 값으로 나눈 값과 같습니다. 분산에 대한 가설 검정 통계량은 카이제곱 분포를 갖습니다.

따라서 분산에 대한 가설 검정 통계량을 계산하는 공식은 다음과 같습니다.

$\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

금:

$\chi^2$

카이제곱 분포를 갖는 분산에 대한 가설 검정 통계입니다.
$n$

표본 크기입니다.
$s^2$

표본 분산입니다.
$\sigma^2$

제안된 모집단 분산입니다.

통계 결과를 해석하려면 얻은 값을 테스트의 임계값과 비교해야 합니다.

분산에 대한 가설 검정이 양측 검정인 경우 통계량이 임계값보다 크면 귀무가설이 기각됩니다.
$\chi_{1-\alpha/2|n-1}^2$

또는 임계값이 다음보다 작은 경우

$\chi_{\alpha/2|n-1}$

.
분산에 대한 가설 검정이 오른쪽 꼬리와 일치하는 경우 통계량이 임계값보다 크면 귀무가설이 기각됩니다.
$\chi_{1-\alpha|n-1}^2$

.
분산에 대한 가설 검정이 왼쪽 꼬리와 일치하는 경우 통계량이 임계값보다 작으면 귀무가설이 기각됩니다.
$\chi_{\alpha|n-1}$

.

$\begin{array}{l}H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha/2|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2\neq \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si }\chi^2<\chi^2_{\alpha/2|n-1}\text{ se rechaza } H_0 \\[3ex]H_1: \sigma^2> \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2>\chi^2_{1-\alpha|n-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma^2< \sigma_0 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } \chi^2<\chi^2_{\alpha|n-1}\text{ se rechaza } H_0\end{array}$

분산에 대한 임계 가설 검정 값은 카이제곱 분포표에서 얻습니다. 카이제곱 분포의 자유도는 표본 크기에서 1을 뺀 값입니다.

분산에 대한 가설 검정의 실제 예

분산가설검정의 정의와 공식이 무엇인지 살펴본 후, 구체적인 예를 통해 개념의 이해를 마무리하겠습니다.

한 공장에 자동차 부품을 고정밀도로 생산하는 기계가 있습니다. 하지만 이제는 다른 곳으로 이전해 ^8mm2 이상의 간격을 가진 부품을 생산하고 있는 것으로 의심된다. 이 가설을 반박하기 위해 25개의 표본을 분석했는데 표본 분산은 9.1 mm ² 입니다. 유의수준 α=0.05에서 초기 가설을 기각할 수 있습니까?

본 분산가설 검정에 대한 귀무가설과 대립가설은 다음과 같습니다.

$\begin{cases}H_0: \sigma^2=8 \\[2ex] H_1:\sigma^2>8 \end{cases}” title=”Rendered by QuickLaTeX.com” height=”65″ width=”101″ style=”vertical-align: 0px;”> 귀무가설이 기각될 수 있는지 여부를 결정하기 위해 위에서 본 공식을 사용하여 분산에 대한 가설 검정 통계량을 계산합니다. <p class=$ $\chi^2=\cfrac{(n-1)s^2}{\sigma^2}$

$\chi^2=\cfrac{(25-1)\cdot 9,1}{8}$

$\chi^2=27,3$

이제 카이제곱 분포표에서 자유도 24도 및 유의 수준 α=0.05에 대한 오른쪽 꼬리에 해당하는 임계값을 찾습니다.

$\begin{array}{c}\chi^2_{1-\alpha|n-1}=\ \color{orange}\bm{?}\color{black}\\[2ex]\chi^2_{0,95|24}=36,415\end{array}$

따라서 계산된 통계량이 검정의 임계값보다 작으므로 분산가설 검정의 귀무가설은 기각되지 않고 오히려 대립가설이 기각됩니다.

$27,3<36,415 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{No se rechaza } H_0$

➤ 참조: 모집단 평균에 대한 가설 검정
➤ 참조: 인구 비율에 대한 가설 검정

두 모집단의 분산에 대한 가설 검정

두 모집단 분산 가설 검정은 서로 다른 두 모집단의 분산이 동일하다는 가설을 기각하거나 승인하는 데 사용됩니다.

따라서 두 모집단의 분산에 대한 가설 검정의 귀무가설은 항상 다음과 같습니다.

$H_0: \sigma^2_1=\sigma^2_2$

대립 가설은 세 가지 옵션 중 하나일 수 있습니다.

$\begin{array}{l}H_1:\sigma^2_1\neq \sigma^2_2\\[2ex]H_1:\sigma^2_1>\sigma^2_2\\[2ex]H_1:\sigma^2_1<\sigma^2_2\end{array}$

이 경우 두 모집단의 분산에 대한 가설 검정 통계량을 계산하는 공식은 다음과 같습니다.

$F=\cfrac{s_1^2}{s_2^2}$

금:

$F$

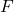
는 F 분포를 따르는 두 모집단의 분산에 대한 가설 검정 통계입니다.
$\sigma_1^2$

모집단 1의 분산입니다.
$\sigma_2^2$

모집단 2의 분산입니다.
$s_1^2$

표본 1의 분산입니다.
$s_2^2$

표본 2의 분산입니다.
$n_1$

표본 크기는 1입니다.
$n_2$

표본 크기는 2입니다.

Snedecor F 분포는 대칭이 아니므로 다음 기준에 따라 귀무 가설이 기각됩니다.

[latex]\begin{배열}{l}H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow}\color{black} \ \text{Si } F>F_{ 1-\alpha/2|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2\neq \sigma_2^2 \ \color{orange}\bm{\longrightarrow }\color{검은색} \ \text{If }F \sigma_2^2 \ \color{주황색}\bm{\longrightarrow}\color{검은색} \ \text{If } F>F_{1-\alpha|n_1-1|n_2-1}\text{ se rechaza } H_0\\[3ex]H_1: \sigma_1^2< \sigma_2^2 \ \color{주황색}\bm{\longrightarrow}\color{검정색} \ \text{Si } F

저자 소개

벤자민 앤더슨

안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기