중심 극한 정리
이 기사에서는 중심 극한 정리(CLT)가 무엇인지, 통계에서 어떤 용도로 사용되는지 설명합니다. 또한 중심극한정리의 공식이 무엇인지, 그리고 그 적용 예를 단계별로 풀어볼 수 있습니다.
중심극한정리란 무엇인가?
통계에서 중심 극한 정리 라고도 하는 중심 극한 정리는 모집단의 확률 분포 에 관계없이 표본 크기가 증가함에 따라 표본 평균의 분포가 정규 분포에 가까워진다는 것을 나타냅니다.
즉, 중심 극한 정리는 충분히 많은 수의 표본을 취하면 해당 표본의 평균이 정규 분포에 가까워질 수 있다고 말합니다.
또한 중심 극한 정리에 따르면 표본 크기가 증가함에 따라 표본 평균이 모집단 평균 값에 가까워집니다. 이를 통해 우리는 통계적 모집단의 매개변수를 근사화할 수 있습니다. 아래에서 이것이 어떻게 수행되는지 살펴보겠습니다.
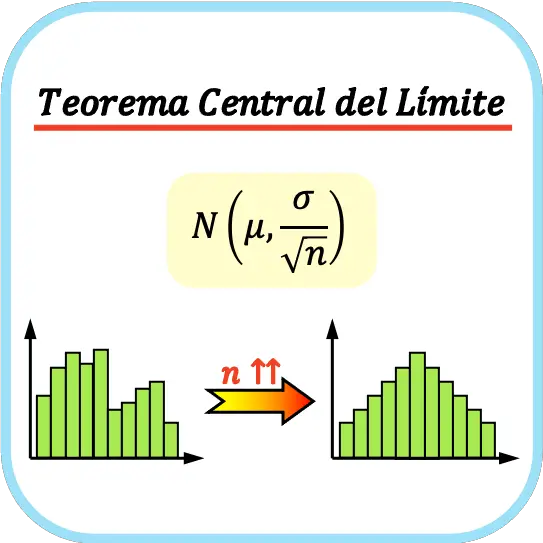
일반적으로 중심극한정리를 적용하기 위해서는 연구변수의 특성에 따라 다르지만 표본크기는 최소 30개 이상의 관측치가 필요하다고 생각된다.
중심 극한 정리는 정규 분포를 통해 가설 검정이나 신뢰 구간과 같은 추론 통계 계산이 가능하므로 많은 응용 분야가 있습니다. 예를 들어, 금융에서는 중심 극한 정리를 사용하여 투자 수익과 위험을 분석합니다.
중심 극한 정리의 예
중심극한정리의 정의를 살펴보았다면, 그 의미를 완전히 이해하기 위해 예를 살펴보겠습니다.
중심 극한 정리의 예는 주사위를 굴리는 것입니다. 주사위 굴림은 모든 결과가 동등할 수 있으므로 이산 균일 분포를 따릅니다. 그러나 여러 결과의 합에 대한 분포는 정규 분포에 가깝습니다.
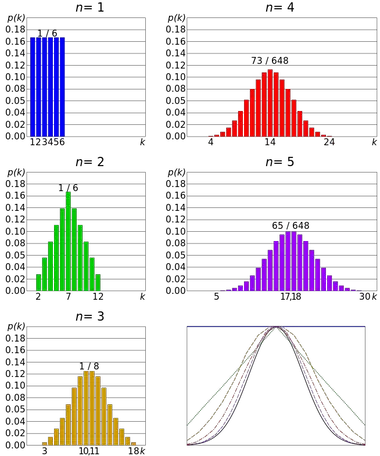
따라서 던진 횟수가 많을수록 평균 분포의 모양이 정규 분포 그래프와 유사한 경향이 있을 가능성이 더 높습니다.
중심 극한 정리 공식
중심 극한 정리는 모집단이 평균 μ 및 표준 편차 σ를 갖고 충분히 많은 수의 표본(n≥30)을 취하는 경우 표본 평균 세트는 평균 μ 및 표준 편차 σ를 갖는 정규 분포에 근접할 수 있음을 나타냅니다. /√n.
![]()
또한 , X 1 인 경우 다음 공식으로 정의되는 정규 분포가 됩니다.
![]()
중심 극한 정리의 해결 운동
개념을 완전히 이해할 수 있도록 중심 극한 정리의 해결 연습이 있습니다.
- 한 회사에서 특정 장난감 부품을 교체하는 데 사용되는 부품을 판매합니다. 동전의 평균 무게는 300g이고 표준편차는 50g입니다. 고객이 100개의 배치를 주문한 경우 배치에 포함된 조각의 평균 무게가 305g보다 클 확률은 얼마입니까? 그리고 100개 묶음의 무게가 31kg을 초과할 확률은 얼마입니까?
배치 크기가 크기 때문에(n=100) 중심 극한 정리를 적용하여 문제를 해결할 수 있습니다.
따라서 중심 극한 정리 공식을 사용하면 표본 평균의 분포는 다음 매개변수를 사용하여 정규 분포에 근접할 수 있습니다.
![]()
![]()
![]()
![]()
이제 우리는 연습에서 요구하는 확률을 찾을 수 있도록 타이핑 프로세스를 수행합니다. 이렇게 하려면 분포에서 평균을 뺀 다음 표준편차로 나누어야 합니다.
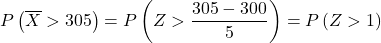 정규 분포표 에서 Z>1 값이 어떤 값에 해당하는지 살펴봐야 합니다.
정규 분포표 에서 Z>1 값이 어떤 값에 해당하는지 살펴봐야 합니다.
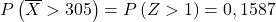
![]()
![]()
![]()
따라서 우리는 타이핑 과정을 다시 실행한 다음 문제가 우리에게 묻는 두 번째 확률을 찾습니다.
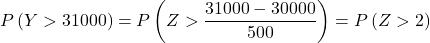
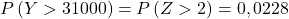 ➤ 참고: 대수의 법칙
➤ 참고: 대수의 법칙