실험적 확률

여기에서는 실험 확률의 의미와 실험 확률 계산 방법을 알아봅니다. 또한 실험적 확률을 계산하는 단계별 해결 사례를 볼 수 있습니다.

실험적 확률이란 무엇입니까?

실험확률(Experimental Probability) 은 실험의 결과나 경험적 사실을 바탕으로 한 통계적 척도로서 어떤 사건이 발생할 확률을 나타낸다.

또한 실험을 반복할수록 실험 확률이 더 정확해집니다. 이러한 이유로 실험 확률을 결정하기 위해서는 일반적으로 수천 번의 실험을 빠르게 시뮬레이션할 수 있는 컴퓨터 프로그램을 사용하여 더 나은 정확도를 얻습니다.

실험 확률은 경험적 확률 또는 빈도 확률 이라고도 합니다.

실험 확률은 0에서 1 사이의 숫자입니다. 논리적으로 어떤 사건의 실험 확률 값이 클수록 발생할 가능성이 높고, 반대로 값이 작을수록 발생할 가능성이 적습니다. 발생할 가능성이 높습니다. 또는 이벤트가 발생합니다. 그러나 실험 확률의 값은 항상 0과 1 사이입니다.

실험적 확률 공식

실험 확률의 공식은 실험 중에 사건이 발생한 횟수를 실험이 수행된 총 횟수로 나눈 것입니다.

예를 들어, 한 사람이 목표물에 10개의 다트를 던지고 중앙에 6개의 다트를 맞추는 경우, 그 사람이 중앙에 다트를 칠 확률은 다음과 같이 계산됩니다.

실험적 확률의 예

실험적 확률의 수학적 정의를 확인한 후에는 이러한 유형의 확률에 대한 단계별 연습을 해결해 보겠습니다. 목표는 사건의 실험 확률이 어떻게 계산되는지 배우는 것이므로 질문이 있는 경우 댓글에 적어주세요.

• 주사위를 굴리는 무작위 실험을 구성하는 기본 사건의 실험 확률을 계산합니다.

실험 확률을 찾기 전에, 이론적 확률을 계산하여 얻은 실험 결과와 이론적 결과를 비교하겠습니다. 잘 아시다시피, 주사위를 굴릴 때 가능한 결과는 6가지(1, 2, 3, 4, 5, 6)이므로 각 기본 사건의 이론적 확률은 다음과 같습니다.

이 연습문제를 해결하려면 주사위 굴리기를 여러 번 시뮬레이션하고 그 결과를 분할표에 기록해야 합니다. 이 경우에는 엑셀 프로그램으로 시뮬레이션을 하겠지만, 당연히 원하는 프로그램을 사용해도 됩니다.

먼저 10번의 던지기, 그 다음에는 100번의 던지기, 마지막으로 1000번의 던지기를 시뮬레이션합니다. 이렇게 하면 결과를 분석하고 실험의 표본 크기에 따라 결과가 어떻게 변하는지 확인할 수 있습니다. 10번의 주사위 던지기에 대한 무작위 시뮬레이션 후 얻은 결과는 다음과 같습니다.

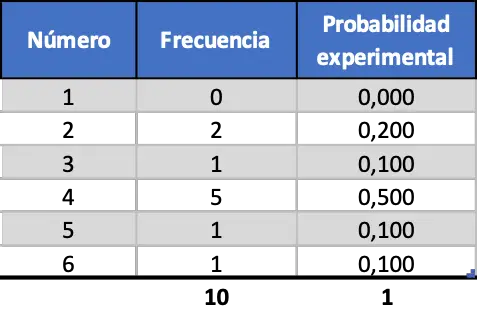
보시다시피, 현재 얻은 실험 확률은 이전에 계산된 이론적 확률(0.167)과 상당히 다릅니다.

그러나 테스트 횟수가 늘어날수록 이 두 측정항목은 더욱 유사해집니다. 100번의 출시 시뮬레이션을 살펴보세요.

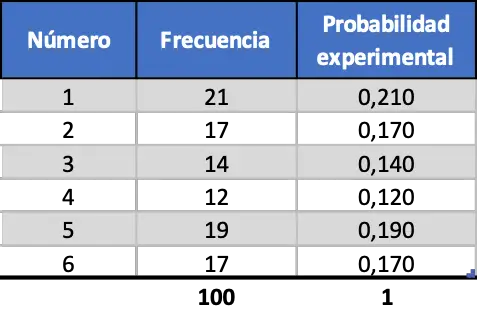
이제 실험 확률은 이론적 확률 값과 더 비슷해 보이지만 여전히 멀리 있는 값을 얻습니다.

마지막으로 동일한 절차를 수행하지만 1000번의 실행을 시뮬레이션합니다.

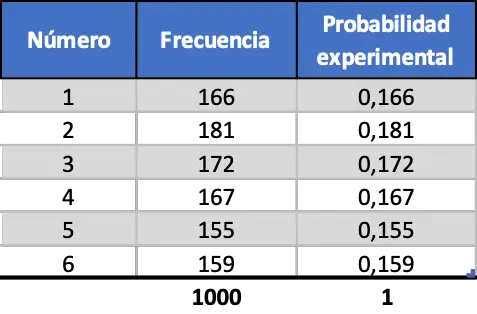
마지막 분할표에서 볼 수 있듯이 이제 실험 확률의 값은 이론 확률과 매우 유사합니다.

요약하면, 수행된 실험 수가 많을수록 사건의 실험 확률 값은 이론 확률에 더 가까워집니다 . 이 규칙은 데이터가 많을수록 실험값이 이론값에 가까워진다는 대수의 법칙 으로 정의됩니다.

마찬가지로, 세 가지 빈도표를 비교해 보면 실험 확률이 확정적이지 않고, 수행되는 실험 횟수에 따라 진화한다는 것을 알 수 있습니다. 즉, 얻은 값을 해석하는 방법을 알아야 한다는 뜻입니다.

실험적 확률과 이론적 확률

실험적 확률과 이론적 확률(또는 고전적 확률)의 차이는 실험적 확률은 실제 실험에서 수집한 데이터로부터 계산되는 반면, 이론적 확률은 실험을 수행할 필요 없이 계산된다는 점입니다.

우리가 본 것처럼, 사건의 실험적 확률을 추론하기 위해서는 수많은 실험을 시뮬레이션해야 합니다. 그러나 이론적 확률을 계산하는 것은 이론과 논리와 관련이 있습니다. 여기에서 어떻게 완료되었는지 확인할 수 있습니다.