Excel: 회귀 계수에 대한 신뢰 구간 계산

선형 회귀 모델에서 회귀 계수는 예측 변수의 1단위 증가와 관련된 응답 변수 의 평균 변화를 알려줍니다.

다음 공식을 사용하여 회귀 계수에 대한 신뢰 구간을 계산할 수 있습니다.

β ₁ 에 대한 신뢰구간: b ₁ ± t _{1-α/2, n-2} * se(b ₁ )

금:

•   b ₁ = 회귀표에 표시된 회귀계수
• t _{1-∝/2, n-2} = 자유도가 n-2인 1-∝ 신뢰 수준에 대한 임계 t 값입니다. 여기서 n 은 데이터 세트의 총 관측 수입니다.
• se(b ₁ ) = 회귀표에 표시된 b ₁ 의 표준 오차

다음 예에서는 Excel에서 회귀 계수에 대한 신뢰 구간을 계산하는 방법을 보여줍니다.

예: Excel의 회귀 계수에 대한 신뢰 구간

특정 수업의 15명의 학생에 대한 학습 시간을 예측 변수로 사용하고 시험 점수를 응답 변수로 사용하여 간단한 선형 회귀 모델을 적합화한다고 가정합니다.

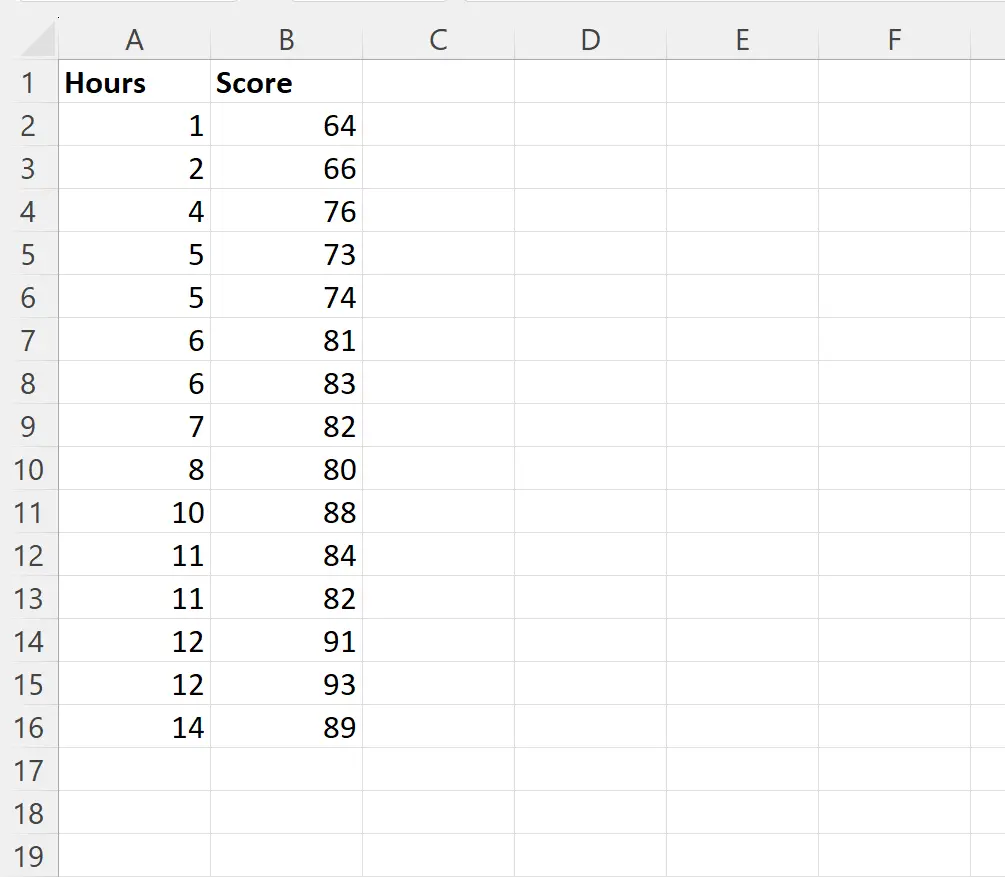
D2 셀에 다음 수식을 입력하면 Hours 열의 값을 예측 변수로 사용하고 Score 열의 값을 응답 변수로 사용하여 단순 선형 회귀를 수행할 수 있습니다.

 =LINEST( B2:B16 , A2:A16 , TRUE, TRUE)

첫 번째 TRUE 인수는 Excel에 회귀 방정식의 절편을 0으로 강제하지 않고 일반적으로 계산하도록 지시합니다.

두 번째 TRUE 인수는 Excel에 계수 외에 추가 회귀 통계를 생성하도록 지시합니다.

다음 스크린샷은 이 수식의 결과를 보여줍니다. 각 출력 값이 출력 아래 빨간색 텍스트로 무엇을 나타내는지 설명합니다.

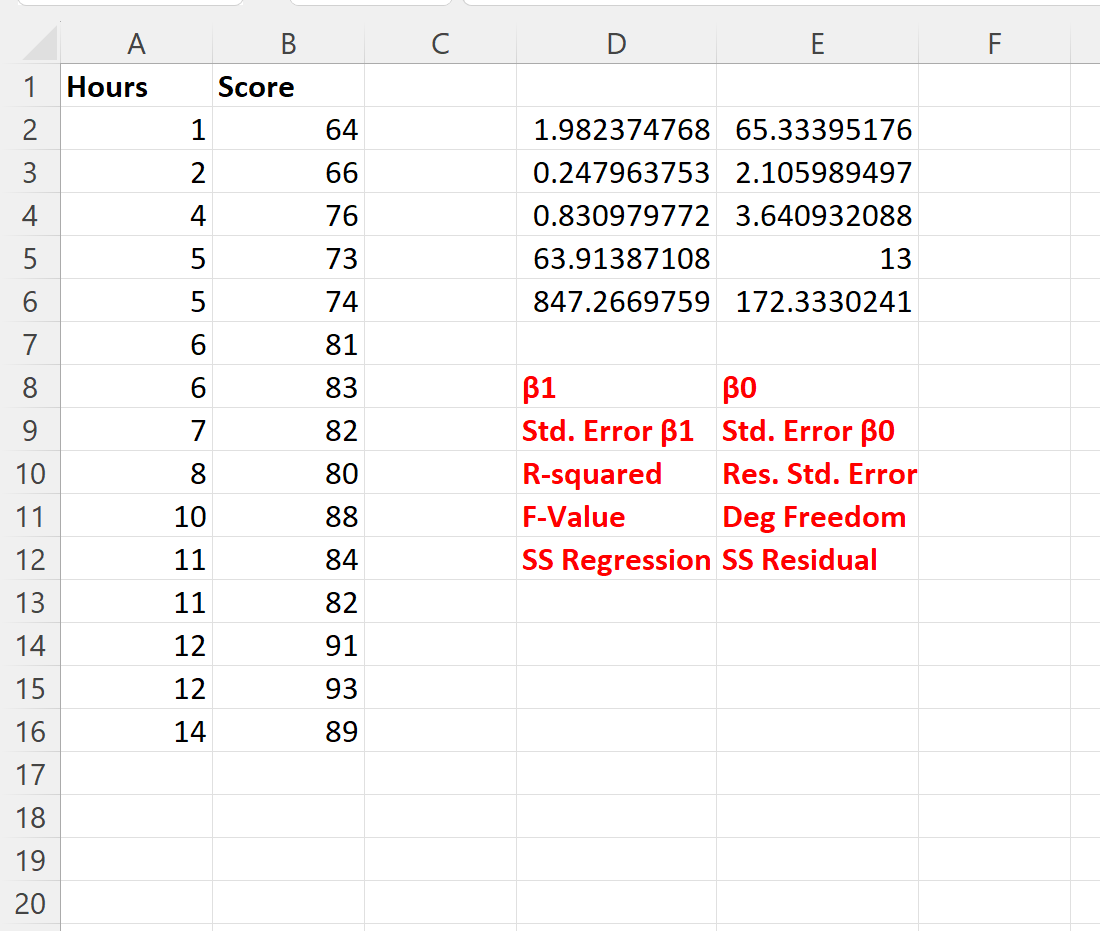
회귀 계수를 사용하여 다음과 같이 적합 회귀 방정식을 작성할 수 있습니다.

점수 = 65.334 + 1.982*(공부한 시간)

시간에 대한 회귀계수는 1.982 입니다.

이는 학습 시간이 추가될 때마다 시험 점수가 평균 1,982 점 증가하는 것과 관련이 있음을 알려줍니다.

회귀 계수에 대한 95% 신뢰 구간을 계산하려면 셀 H2 및 H3에 다음 수식을 입력할 수 있습니다.

• H2: = D2 – T.INV.2T(0.05, E5)*D3
• H3: = D2 + T.INV.2T(0.05, E5)*D3

다음 스크린샷은 실제로 이러한 수식을 사용하는 방법을 보여줍니다.

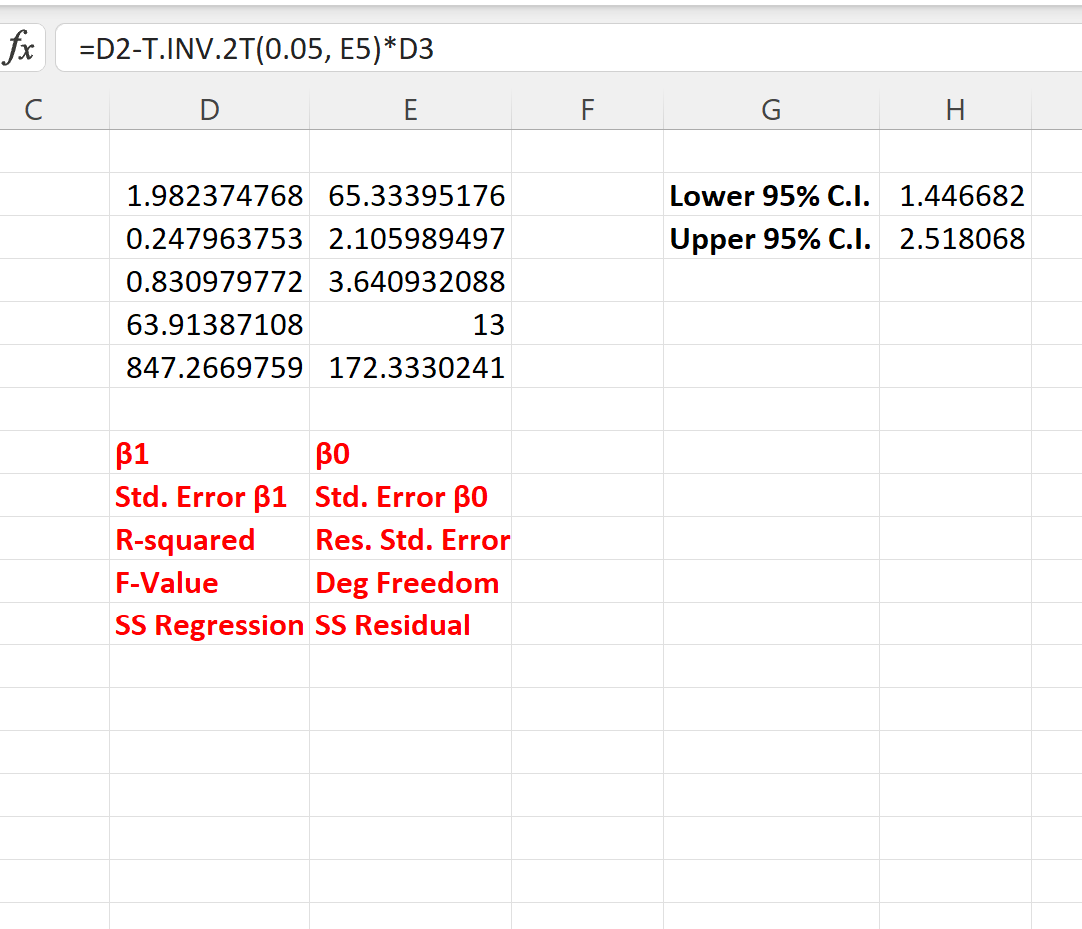
회귀계수의 95% 신뢰구간은 [1.446, 2.518] 입니다.

이 신뢰 구간에는 0 값이 포함되어 있지 않으므로 공부 시간과 시험 성적 사이에 통계적으로 유의미한 연관성이 있다는 결론을 내릴 수 있습니다.

회귀 계수에 대한 95% 신뢰 구간을 수동으로 계산하여 이것이 올바른지 확인할 수도 있습니다.

• β ₁ 에 대한 95% CI : b ₁ ± t _{1-α/2, n-2} * se(b ₁ )
• β ₁ 에 대한 95% CI: 1.982 ± t _{0.975, 15-2} * 0.248
• β ₁ 에 대한 95% CI: 1.982 ± 2.1604 * 0.248
• β ₁ 에 대한 95% CI: [1.446, 2.518]

회귀계수의 95% 신뢰구간은 [1.446, 2.518] 입니다.

추가 리소스

다음 자습서에서는 Excel에서 다른 일반적인 작업을 수행하는 방법을 설명합니다.

Excel에서 단순 선형 회귀를 수행하는 방법
Excel에서 다중 선형 회귀를 수행하는 방법
Excel에서 회귀 출력의 P 값을 해석하는 방법