Excel의 z 점수에서 p 값을 찾는 방법

통계의 많은 가설 검정은 z-검정 통계를 생성합니다. 이 z-검정 통계를 찾으면 일반적으로 이와 관련된 p-값을 찾습니다. 이 p-값이 특정 알파 수준(예: 0.10, 0.05, 0.01)보다 낮으면 검정의 귀무 가설을 기각하고 결과가 유의하다는 결론을 내립니다.

이 튜토리얼에서는 다음 인수를 사용하는 NORM.DIST 함수를 사용하여 Excel의 z-점수에서 p-값을 찾는 몇 가지 예를 보여줍니다.

NORM.DIST (x, 평균, 표준_개발, 누적)

금:

• x 는 우리가 관심을 갖는 z 점수입니다.
• 평균 은 분포의 평균입니다. 표준 정규 분포에는 “0”을 사용합니다.
• Standard_dev 는 분포의 표준 편차입니다. 표준 정규 분포에는 “1”을 사용합니다.
• cumulative는 “TRUE”(CDF 반환) 또는 “FALSE”(PDF 반환) 값을 취합니다. 누적 분포 함수의 값을 얻으려면 “TRUE”를 사용합니다.

몇 가지 예를 살펴보겠습니다.

예시 1: Z 점수에서 P 값 찾기(양측 검정)

한 회사는 새로운 유형의 배터리가 평균 수명이 18시간인 현재 표준 배터리와 평균 수명이 다른지 알고 싶어합니다. 100개의 새 배터리에 대한 무작위 표본 에서 평균 수명은 19시간이고 표준 편차는 4시간입니다.

새 배터리의 평균 수명이 현재 표준 배터리의 평균 수명과 다른지 여부를 확인하기 위해 알파 수준 0.05를 사용하여 양측 가설 검정을 수행합니다.

1단계: 가설을 진술합니다.

귀무가설(H ₀ ): μ = 18

대립 가설: (Ha): μ ≠ 18

2단계: z-테스트 통계량을 찾습니다.

검정 통계량 z = (x-μ) / (s/√n) = (19-18) / (4/√100) = 2.5

3단계: Excel을 사용하여 z-검정 통계의 p-값을 찾습니다.

z = 2.5에 대한 p-값을 찾기 위해 Excel에서 다음 공식을 사용합니다: =1 – NORM.DIST(2.5, 0, 1, TRUE)

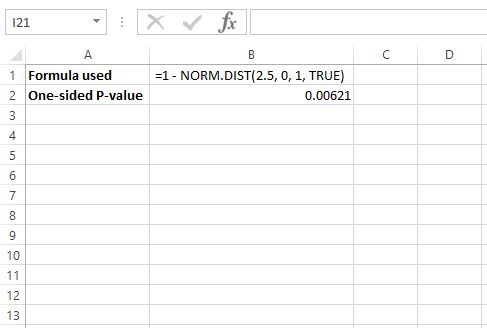
이는 단측 p-값이 .00621 이라는 것을 말하지만, 양측 테스트를 수행하고 있으므로 이 값에 2를 곱해야 하므로 p-값은 .00612 * 2 = .01224 가 됩니다.

4단계: 귀무가설을 기각하거나 기각하지 않습니다.

p-값 0.01224가 선택한 알파 수준 0.05 보다 작으므로 귀무 가설을 기각합니다. 새 배터리의 평균 수명이 기존 표준 배터리의 평균 수명과 크게 다르다고 말할 수 있는 충분한 증거가 있습니다.

예시 2: Z 점수에서 P 값 찾기(단측 검정)

한 식물학자는 특정 식물의 평균 키가 14인치 미만이라고 추정합니다. 그녀는 무작위로 30개의 식물을 선택하여 측정합니다. 그녀는 평균 키가 13.5인치이고 표준 편차가 2인치라는 것을 발견했습니다.

이 식물의 평균 높이가 실제로 14인치보다 작은지 확인하려면 알파 수준 0.01을 사용하여 단측 가설 검정을 수행하십시오.

1단계: 가설을 진술합니다.

귀무가설(H0): μ≥ 14

대립 가설: (Ha): μ < 14

2단계: z-테스트 통계량을 찾습니다.

검정 통계량 z = (x-μ) / (s/√n) = (13.5-14) / (2/√30) = -1.369

3단계: Excel을 사용하여 z-검정 통계의 p-값을 찾습니다.

z = -1.369에 대한 p-값을 찾기 위해 Excel에서 다음 공식을 사용합니다: =NORM.DIST(-1.369, 0, 1, TRUE)

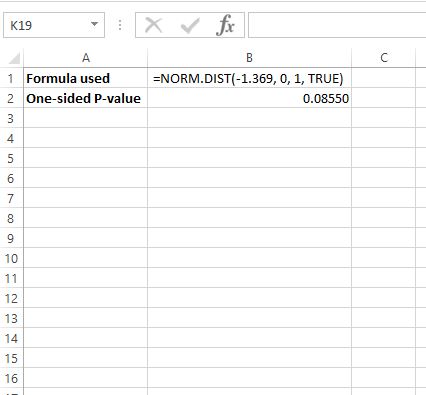
이는 단측 p-값이 0.08550 임을 알려줍니다.

4단계: 귀무가설을 기각하거나 기각하지 않습니다.

p-값 0.08550 이 선택한 알파 수준 0.01 보다 크기 때문에 귀무 가설을 기각할 수 없습니다. 이 식물 종의 평균 키가 14인치 미만이라고 말할 수 있는 충분한 증거가 없습니다.

Excel 통계에 대한 추가 자습서를 보려면 Excel 가이드 전체 목록을 확인하세요 .