Stata에서 manova를 수행하는 방법

일원 분산 분석은 설명 변수의 수준이 다르면 특정 반응 변수에서 통계적으로 다른 결과가 나오는지 여부를 확인하는 데 사용됩니다.

예를 들어, 세 가지 교육 수준(준학사 학위, 학사 학위, 석사 학위)이 통계적으로 다른 연간 수입으로 이어지는지 여부를 이해하는 데 관심이 있을 수 있습니다. 이 경우에는 설명 변수와 반응 변수가 있습니다.

• 설명변수: 교육수준
• 반응변수: 연소득

MANOVA 는 둘 이상의 반응 변수가 있는 일원 분산 분석의 확장입니다. 예를 들어, 교육 수준에 따라 연간 소득이 달라 지고 학자금 부채 금액이 달라지는지 여부를 이해하는 데 관심이 있을 수 있습니다. 이 경우에는 하나의 설명 변수와 두 개의 응답 변수가 있습니다.

• 설명변수: 교육수준
• 반응변수: 연소득, 학자금 빚

반응 변수가 두 개 이상 있으므로 이 경우에는 MANOVA를 사용하는 것이 적절할 것입니다.

다음으로 Stata에서 MANOVA를 수행하는 방법을 설명하겠습니다.

예: Stata의 MANOVA

Stata에서 MANOVA를 수행하는 방법을 설명하기 위해 24명에 대한 다음 세 가지 변수가 포함된 다음 데이터 세트를 사용합니다.

• educ: 학업 수준(0 = 준학사, 1 = 학사, 2 = 석사)
• 소득: 연간 소득
• 부채: 총 학자금 대출 부채

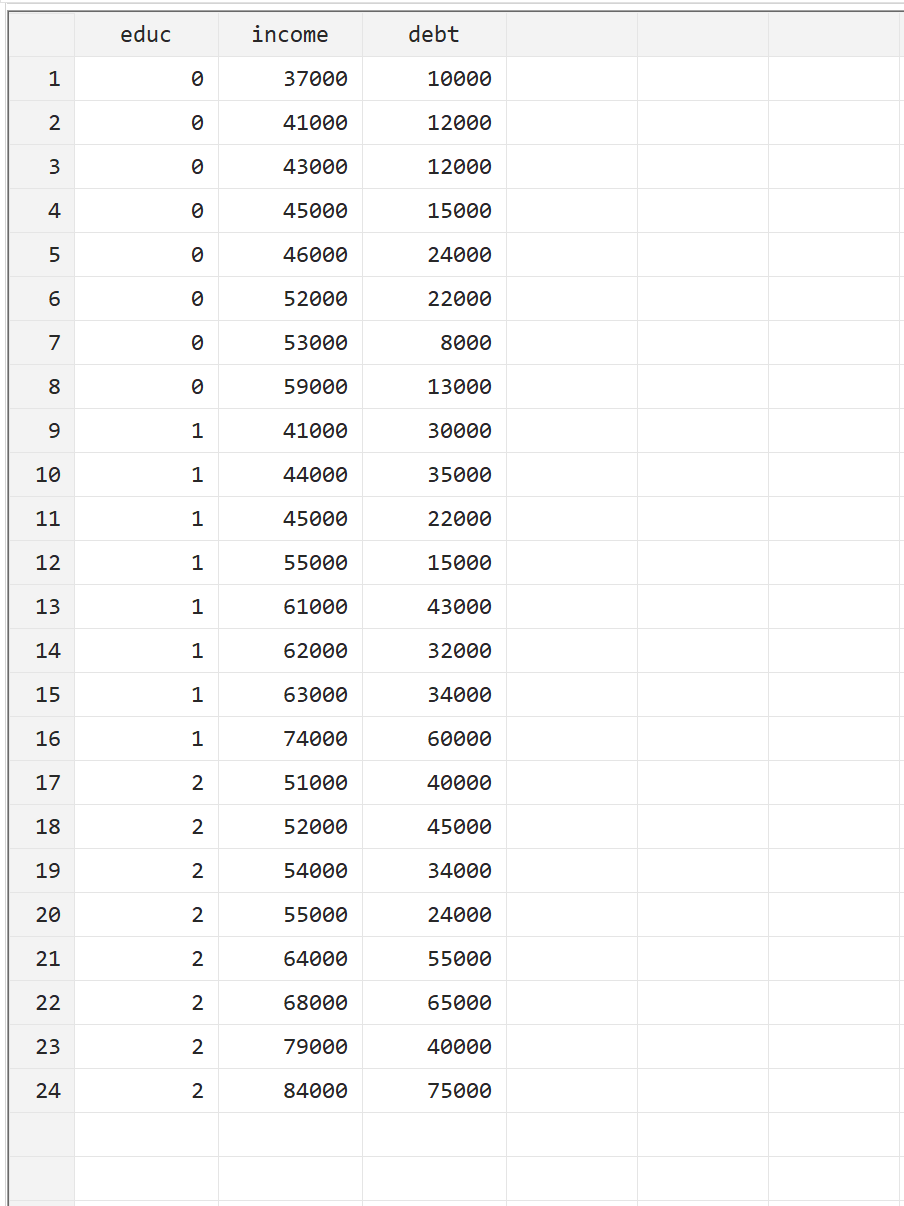
상단 메뉴바에서 데이터 > 데이터 편집기 > 데이터 편집기(편집) 로 이동하여 직접 데이터를 입력하여 이 예를 재현할 수 있습니다.

교육을 설명 변수로, 소득과 부채를 반응 변수로 사용하여 MANOVA를 수행하려면 다음 명령을 사용할 수 있습니다.

소득 부채 manova = 교육

Stata는 해당 p-값과 함께 4가지 고유한 테스트 통계를 생성합니다.

Wilks의 람다: F 통계 = 5.02, P 값 = 0.0023.

Pillai 추적: F 통계 = 4.07, P 값 = 0.0071.

Lawley-Hotelling 추적: F 통계 = 5.94, P 값 = 0.0008.

가장 큰 Roy 루트: F-통계 = 13.10, P-값 = 0.0002.

각 테스트 통계가 계산되는 방법에 대한 자세한 설명은 Penn State Eberly College of Science의 이 기사를 참조하세요.

각 검정 통계량의 p-값은 0.05보다 작으므로 어떤 가설을 사용하더라도 귀무 가설은 기각됩니다. 이는 교육 수준이 연간 소득과 총 학생 부채에 통계적으로 유의미한 차이를 가져온다고 말할 수 있는 충분한 증거가 있음을 의미합니다.

p-값에 대한 참고 사항: 출력 표에서 p-값 옆에 있는 문자는 F 통계가 계산된 방법을 나타냅니다(e = 정확한 계산, a = 대략적인 계산, u = 상한).