사분위수

이 글에서는 사분위수가 무엇인지 설명합니다. 각 사분위수의 정의, 계산 방법 및 몇 가지 구체적인 예를 확인할 수 있습니다. 또한 그룹화된 데이터의 사분위수를 계산하는 방법도 보여줍니다. 또한 온라인 계산기를 사용하여 모든 데이터 세트의 사분위수를 계산할 수 있습니다.

사분위수란 무엇입니까?

통계에서 사분위수는 정렬된 데이터 집합을 4개의 동일한 부분으로 나누는 세 가지 값입니다. 따라서 첫 번째, 두 번째, 세 번째 사분위수는 각각 전체 통계 데이터의 25%, 50%, 75%를 나타냅니다.

사분위수는 대문자 Q와 사분위수 지수로 표시되므로 첫 번째 사분위수는 Q ₁ , 두 번째 사분위수는 Q ₂ , 세 번째 사분위수는 Q ₃ 입니다.

👉 아래 계산기를 사용하여 모든 데이터 세트의 사분위수를 계산할 수 있습니다.

사분위수는 오분위수, 십분위수, 백분위수와 같은 방식으로 비중심 위치를 측정한다는 점에 유의해야 합니다. 이 웹페이지에서 각 분위수 유형이 무엇인지 확인할 수 있습니다.

첫 번째 사분위수

사분위수 1이라고도 하는 첫 번째 사분위수는 표본에 있는 통계 데이터의 25%보다 큰 값입니다. 즉, 첫 번째 사분위수는 관측된 데이터의 25% 이상을 나타냅니다.

첫 번째 사분위수는 _Q1 기호로 표시되며 표본에서 가장 작은 데이터 값을 나타내는 데 사용됩니다.

두 번째 사분위수

2사분위수라고도 하는 두 번째 사분위수 는 표본에 있는 통계 데이터의 50%보다 큰 값입니다. 따라서 두 번째 사분위수는 데이터 세트를 두 부분으로 분리하고 중앙값 및 다섯 번째 십분위수와 일치합니다.

두 번째 사분위수의 기호는 _Q2 입니다.

3분위수

3분위수 라고도 불리는 3분위수는 표본 내 통계 데이터의 75%를 초과하는 값입니다. 즉, 3분위수는 수집된 데이터의 75% 이상을 나타냅니다.

세 번째 사분위수는 _Q3 기호로 표시되며 표본에서 가장 큰 값을 나타냅니다.

사분위수를 계산하는 방법

통계 데이터 세트의 사분위수 위치를 계산 하려면 사분위수에 전체 데이터 수의 합에 1을 더한 값을 곱하고 그 결과를 4로 나누어야 합니다.

따라서 사분위수의 공식은 다음과 같습니다.

참고: 이 공식은 사분위수 값이 아닌 사분위수 위치를 알려줍니다. 사분위수는 공식으로 얻은 위치에 있는 데이터입니다.

그러나 때로는 이 공식의 결과가 십진수를 제공할 수도 있습니다. 따라서 결과가 십진수인지 아닌지에 따라 두 가지 경우를 구별해야 합니다.

• 수식의 결과가 소수 부분이 없는 숫자 인 경우 사분위수는 위 수식에서 제공하는 위치에 있는 데이터입니다.
• 수식 결과가 소수 부분이 있는 숫자 인 경우 사분위수 값은 다음 수식을 사용하여 계산됩니다.

여기서 x _i 와 x _i+1 은 첫 번째 수식에서 구한 숫자가 위치한 위치의 숫자이고, d 는 첫 번째 수식에서 구한 숫자의 소수 부분입니다.

사분위수를 계산하는 것은 고려해야 할 사항이 많기 때문에 매우 복잡할 수도 있습니다. 그러나 다음 섹션의 두 가지 예를 보면 실제로 얼마나 간단한지 알 수 있습니다.

참고 : 과학계에서는 사분위수를 어떻게 계산하는지에 대한 합의가 이루어지지 않아 이를 조금 다르게 설명하는 통계책을 찾아볼 수 있습니다.

사분위수 계산의 예

사분위수 계산 방법을 완전히 이해하려면 아래에서 두 가지 해결 연습을 참조하세요. 첫 번째 사분위수는 정수이고 두 번째 사분위수는 십진수이므로 어떤 두 사례를 찾을 수 있는지 확인할 수 있습니다.

실시예 1

• 다음 데이터 세트의 3분위수를 계산합니다.

위에서 본 것처럼 사분위수를 결정하는 공식은 다음과 같습니다.

이 경우 n , 총 관측값 수는 15이므로 첫 번째 사분위수를 찾으려면 n을 15로, k 를 1로 바꿔야 합니다.

따라서 첫 번째 사분위수는 정렬된 값 목록의 4번째 위치에 있는 숫자이며, 이 경우 39입니다.

같은 방법으로 계수 k를 2로 대체하여 두 번째 사분위수를 계산합니다.

따라서 2분위수는 정렬된 목록의 8번째 숫자이며 값 48에 해당합니다.

마지막으로 k =3인 공식을 마지막으로 한 번 적용하여 세 번째 사분위수를 계산합니다.

3분위수는 12번째 위치의 데이터, 즉 60에 해당합니다.

실시예 2

• 다음 데이터 계열의 3사분위수를 찾습니다.

이 두 번째 예에는 24개의 관측치가 있으므로 사분위수 공식에서 얻은 숫자는 소수가 됩니다.

먼저 일반 공식에서 1 을 k 로 대체하여 첫 번째 사분위수의 위치를 계산합니다.

하지만 우리는 10진수 6.25를 얻었으므로 첫 번째 사분위수는 6번째 데이터와 7번째 데이터 사이, 즉 각각 22와 25입니다. 따라서 정확한 사분위수를 계산하려면 다음 공식을 적용해야 합니다.

이 경우 x _i 는 22, x _i+1 25이고 d 는 얻은 숫자의 소수 부분, 즉 0.25입니다. 아직:

이제 두 번째 사분위수를 찾기 위해 동일한 절차를 수행합니다.

다시 우리는 공식에서 십진수를 얻습니다. 이 경우에는 12.5입니다. 따라서 데이터 테이블의 49와 50에 해당하는 12번째와 13번째 숫자에 대해 동일한 공식을 사용해야 합니다.

마지막으로 3분위수를 얻기 위해 동일한 과정을 반복합니다.

그러나 숫자 18.75는 숫자 18과 19 사이에 있으므로 3분위수는 이 위치의 값(71과 73) 사이에 있게 됩니다. 보다 정확하게는 다음 식에서 얻는 값이 됩니다.

사분위수 계산기

사분위수를 계산하려면 아래 계산기에 통계 데이터 세트를 연결하세요. 데이터는 공백으로 구분해야 하며 소수점 구분 기호로 마침표를 사용하여 입력해야 합니다.

그룹화된 데이터의 사분위수

데이터가 간격으로 그룹화될 때 사분위수를 계산 하려면 먼저 다음 공식을 사용하여 사분위수가 속하는 간격 또는 빈을 찾아야 합니다.

따라서 사분위수는 절대 누적 빈도가 이전 표현식으로 얻은 숫자보다 바로 큰 간격에 있게 됩니다.

그리고 사분위수가 속하는 간격을 알고 나면 사분위수의 정확한 값을 찾기 위해 다음 공식을 적용해야 합니다.

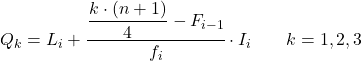
금:

• L _i 는 사분위수가 있는 간격의 하한입니다.
• n 은 총 관측치 수입니다.
• F _i-1 은 이전 구간의 누적 절대 빈도입니다.
• f _i 는 사분위수가 있는 간격의 절대 빈도입니다.
• I _i 는 사분위 간격의 너비입니다.

예를 들어, 다음은 일련의 그룹화된 데이터에서 사분위수를 계산하는 연습입니다.

첫 번째 사분위수를 계산하려면 먼저 해당 사분위수가 속하는 간격을 결정해야 합니다. 이를 위해 다음 공식을 적용합니다.

따라서 첫 번째 사분위수는 누적 절대 빈도가 7.75보다 바로 큰 구간에 있게 됩니다. 이 경우 누적 절대 빈도가 15인 구간 [50.60)입니다. 그리고 사분위수 구간을 알고 나면 두 번째 프로세스 공식을 사용합니다. :

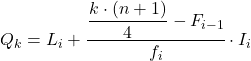
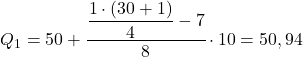
두 번째 사분위수를 얻기 위해 동일한 절차를 다시 적용합니다. 먼저 사분위수가 있는 간격을 결정합니다.

누적 절대 빈도가 15.5보다 바로 큰 구간은 [60.70)이며, 누적 절대 빈도는 26입니다. 따라서 두 번째 사분위수는 다음과 같습니다.

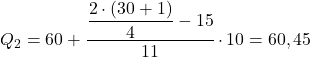
그리고 마지막으로 제3사분위수를 찾기 위해 과정을 반복합니다. 먼저 사분위수를 포함하는 간격을 계산합니다.

23.25 바로 위의 누적 절대 빈도는 26이므로 3분위수 범위는 [60.70)입니다. 따라서 이 간격으로 사분위수를 계산하기 위해 공식을 적용합니다.

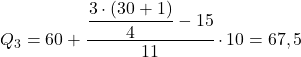
사분위수는 무엇에 사용되나요?

사분위수는 위치의 척도 이므로 데이터의 위치를 파악하는 데 사용됩니다. 즉, 3분위수의 값을 통해 표본의 무작위 데이터 항목이 매우 큰지, 매우 작은지 또는 평균값인지 알 수 있습니다.

표본에서 데이터를 무작위로 추출하면 사분위수와 비교하여 해당 값이 높은지 낮은지 알 수 있습니다. 임의의 데이터 값이 1분위수보다 작으면 작은 값이 되고, 3분위수보다 크면 큰 값이 됩니다. 마찬가지로, 해당 데이터의 값이 1분위수와 3분위수 사이에 있으면 중간 값입니다.

반면, 사분위수는 사분위수 범위(또는 사분위수 범위)와 같은 다른 통계 측정값을 계산하고 상자 수염 플롯(또는 상자 그림)과 같은 다이어그램을 만드는 데에도 사용됩니다.