이항 분포표를 읽는 방법

이항 분포표   이항 분포 와 관련된 확률을 보여주는 표입니다. 이항 분포표를 사용하려면 다음 세 가지 값만 필요합니다.

• n: 시도 횟수
• r: n번의 시도 동안의 “성공” 횟수
• p: 주어진 시행의 성공 확률

이 세 숫자를 사용하면 이항 분포표를 사용하여 각 시행의 성공 확률이 p 인 경우 n번의 시행 과정에서 정확히 r 번의 성공 확률을 찾을 수 있습니다.

다음 예에서는 이항 분포표를 읽는 방법을 보여줍니다.

실시예 1

질문: 제시카는 자유투 시도의 60%를 성공시켰습니다. 만약 그녀가 6번의 자유투를 성공했다면 정확히 4번의 자유투를 성공할 확률은 얼마입니까?

이 질문에 답하기 위해 n = 6, r = 4, p = 0.60 에 해당하는 이항 분포표에서 값을 찾을 수 있습니다 .

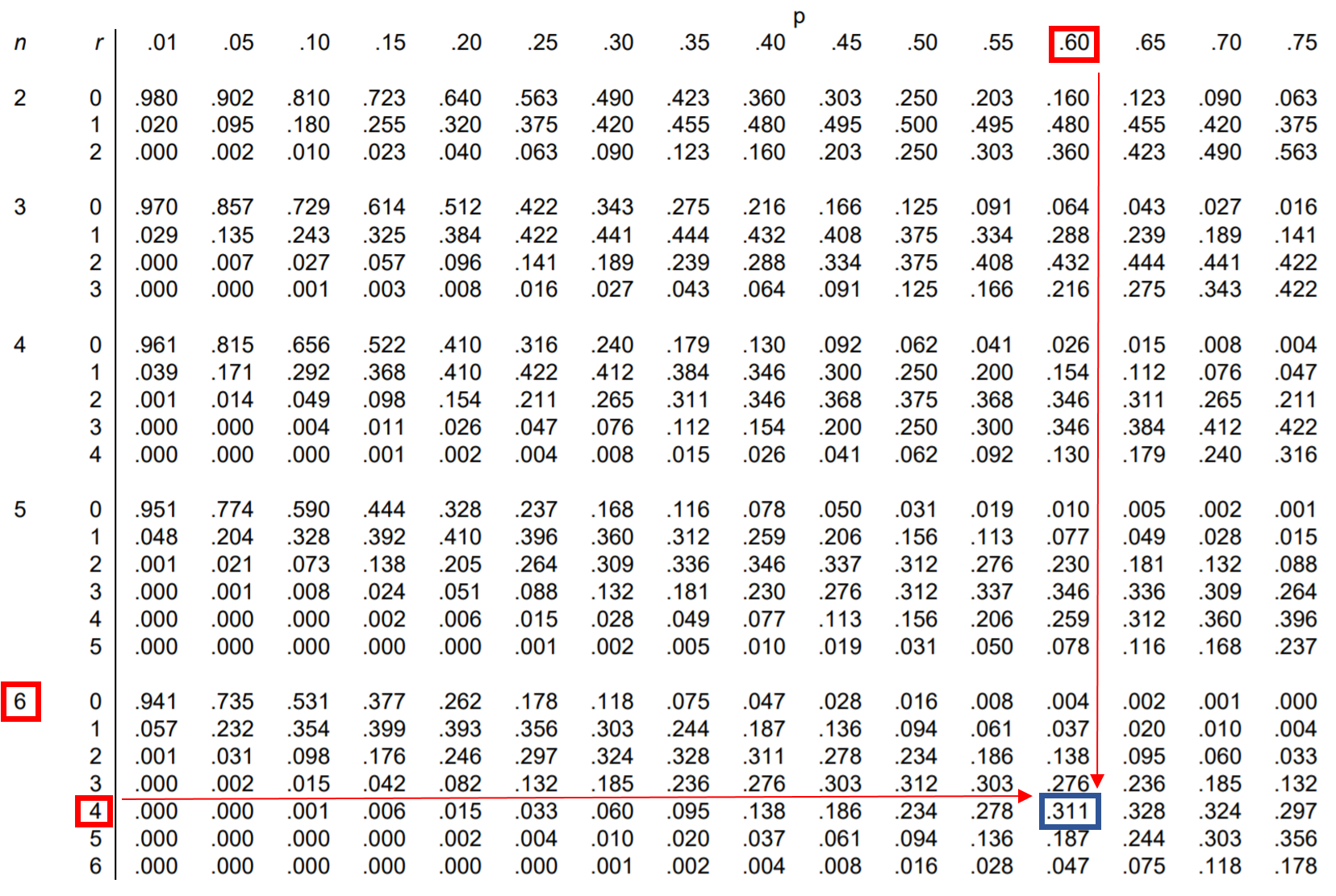
제시카가 6번의 자유투 중 정확히 4번을 성공할 확률은 0.311 입니다.

실시예 2

질문: 제시카는 자유투 시도의 60%를 성공시켰습니다. 만약 그녀가 6개의 자유투를 성공했다면, 4개 미만의 자유투를 성공할 확률은 얼마입니까?

이 확률을 찾으려면 실제로 다음 확률을 추가해야 합니다.

P(4개 미만 만들기) = P(0개 만들기) + P(1개 만들기) + P(2개 만들기) + P(3개 만들기)

따라서 이항 분포표에서 이러한 네 가지 확률을 각각 찾아 더할 수 있습니다.

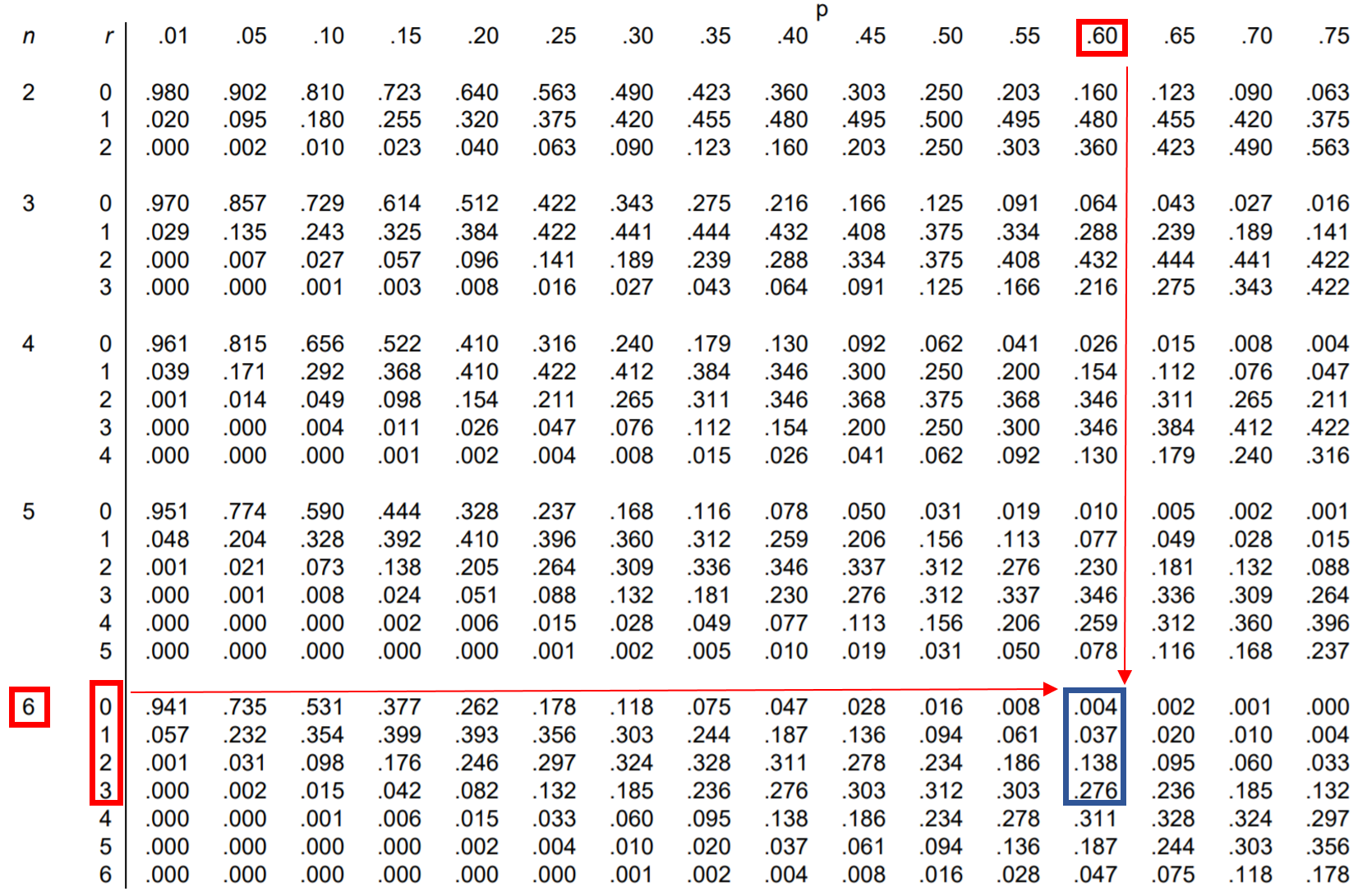
표에서 P(is less than 4) = .004 + .037 + .138 + .276 = 0.455 입니다.

제시카가 4번 미만의 자유투를 성공할 확률은 0.455 입니다.

실시예 3

질문: 제시카는 자유투 시도의 60%를 성공시켰습니다. 만약 그녀가 6번의 자유투를 성공했다면, 4번 이상을 성공할 확률은 얼마나 될까요?

이 확률을 찾으려면 다음 확률을 추가해야 합니다.

P(4개 이상 만들기) = P(4개 만들기) + P(5개 만들기) + P(6개 만들기)

따라서 이항 분포표에서 이러한 세 가지 확률을 각각 찾아 더할 수 있습니다.

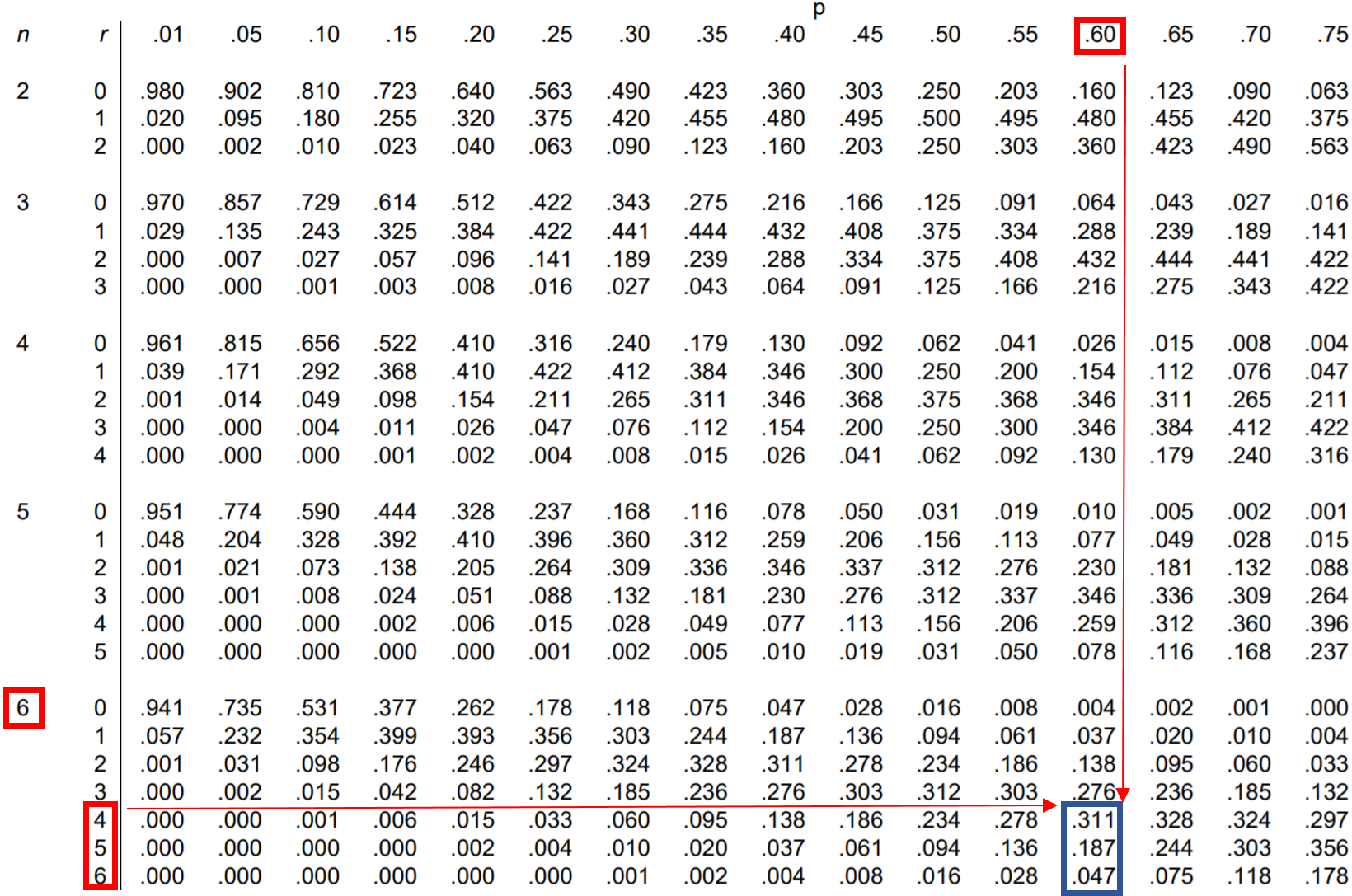
표에서 보면 P(4개 이상 제작) = .311 + .187 + .047 = 0.545 입니다.

제시카가 4번 이상의 자유투를 성공할 확률은 0.545 입니다.