R에서 왜도와 첨도를 계산하는 방법
통계에서 왜도와 첨도는 분포의 모양을 측정하는 두 가지 방법입니다.
왜도는 분포의 왜도를 측정한 것입니다. 이 값은 양수 또는 음수일 수 있습니다.
- 음의 왜도는 꼬리가 분포의 왼쪽에 있고 더 음의 값 쪽으로 확장된다는 것을 나타냅니다.
- 양의 치우침은 꼬리가 분포의 오른쪽에 있고 더 양의 값 쪽으로 확장된다는 것을 나타냅니다.
- 값이 0이면 분포에 비대칭성이 없음을 나타냅니다. 이는 분포가 완벽하게 대칭임을 의미합니다.
첨도는 정규 분포 와 비교하여 분포가 두꺼운 꼬리인지 얇은 꼬리인지를 측정한 것입니다.
- 정규분포의 첨도는 3입니다.
- 주어진 분포의 첨도가 3보다 작은 경우 플레이커틱(playkurtic) 이라고 하며, 이는 정규 분포보다 더 적은 수의 극단적인 이상값을 생성하는 경향이 있음을 의미합니다.
- 특정 분포의 첨도가 3보다 큰 경우 이를 leptokurtic 이라고 합니다. 이는 정규 분포보다 더 많은 이상값을 생성하는 경향이 있음을 의미합니다.
참고: 일부 공식(Fisher 정의)에서는 정규 분포와 더 쉽게 비교할 수 있도록 첨도에서 3을 뺍니다. 이 정의를 사용하면 분포의 첨도 값이 0보다 큰 경우 정규 분포보다 첨도가 더 커집니다.
이 튜토리얼에서는 R에서 주어진 데이터 세트의 왜도와 첨도를 계산하는 방법을 설명합니다.
예: R의 왜도 및 편평화
다음과 같은 데이터 세트가 있다고 가정합니다.
data = c(88, 95, 92, 97, 96, 97, 94, 86, 91, 95, 97, 88, 85, 76, 68)
히스토그램을 생성하여 이 데이터 세트의 값 분포를 빠르게 시각화할 수 있습니다.
hist(data, col=' steelblue ')
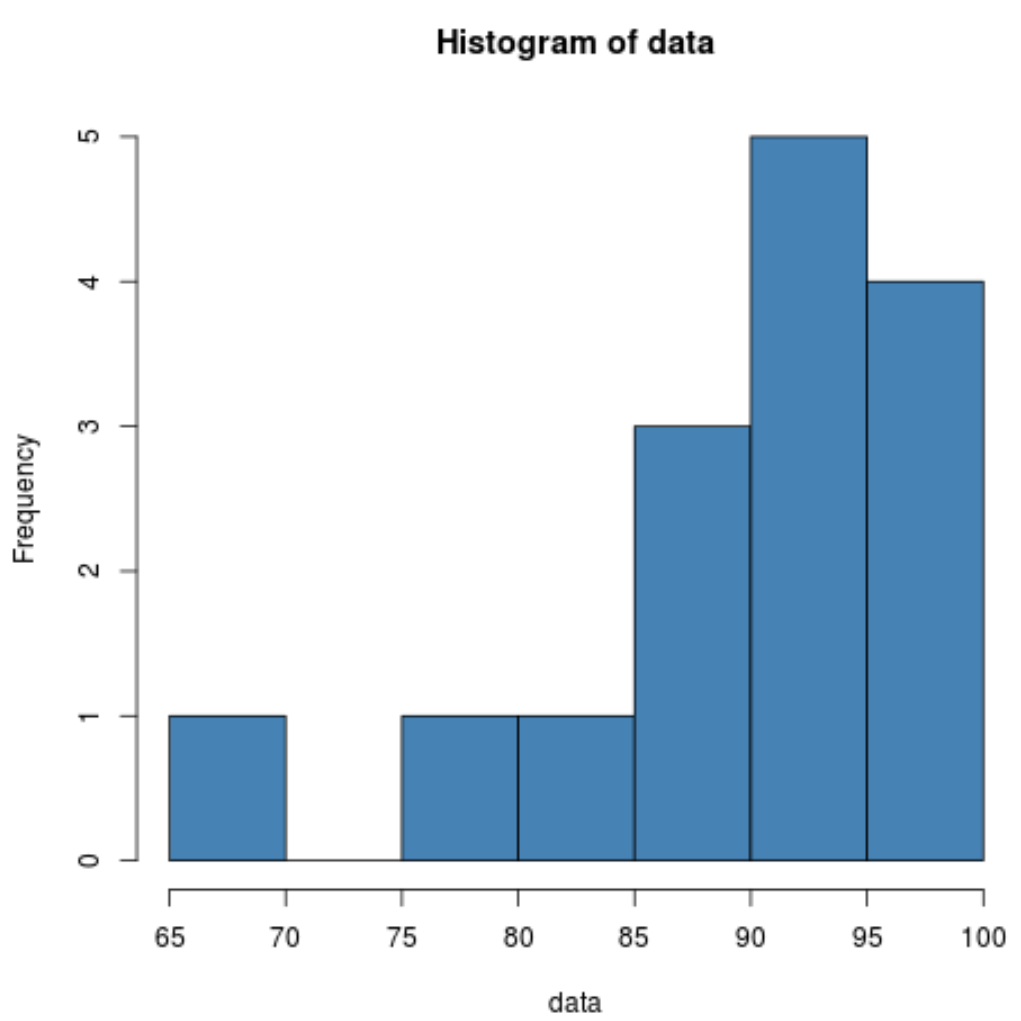
히스토그램을 보면 분포가 왼쪽으로 치우쳐 있는 것처럼 보입니다. 즉, 값의 대부분이 분포의 오른쪽에 집중되어 있습니다.
이 데이터세트의 왜도와 첨도를 계산하려면 R의 모멘트 라이브러리에 있는 Skewness() 및 kurtosis() 함수를 사용할 수 있습니다.
library (moments) #calculate skewness skewness(data) [1] -1.391777 #calculate kurtosis kurtosis(data) [1] 4.177865
왜도는 -1.391777 이고 첨도는 4.177865 입니다.
왜도가 음수이므로 이는 분포가 왼쪽으로 치우쳐 있음을 나타냅니다. 이는 히스토그램에서 본 내용을 확인시켜줍니다.
첨도가 3보다 크므로 이는 정규 분포에 비해 분포의 꼬리에 더 많은 값이 있음을 나타냅니다.
또한 순간 라이브러리는 표본 데이터가 정규 분포와 일치하는 왜도 및 첨도를 나타내는지 여부를 결정하는 적합도 테스트를 수행하는 jarque.test() 함수를 제공합니다. 이 검정의 귀무가설과 대립가설은 다음과 같습니다.
귀무 가설 : 데이터 세트에는 정규 분포에 해당하는 왜도와 첨도가 있습니다.
대립 가설 : 데이터 세트에는 정규 분포에 해당하지 않는 편향과 첨도가 있습니다.
다음 코드는 이 테스트를 수행하는 방법을 보여줍니다.
jarque.test(data)
Jarque-Bera Normality Test
data:data
JB = 5.7097, p-value = 0.05756
alternative hypothesis: greater
테스트의 p-값은 0.05756 으로 나타났습니다. 이 값은 α = 0.05 이상이므로 귀무가설을 기각할 수 없습니다. 이 데이터 세트에 정규 분포와 다른 왜도와 첨도가 있다고 말할 수 있는 충분한 증거가 없습니다.
여기에서 전체 Moments 라이브러리 문서를 찾을 수 있습니다.
보너스: 왜도 및 첨도 계산기
주어진 데이터세트에 대한 왜도와 첨도를 자동으로 계산 하는 통계적 왜도 및 첨도 계산기를 사용하여 주어진 데이터세트에 대한 왜도를 계산할 수도 있습니다 .