R에서 dfbetas를 계산하는 방법

통계에서 우리는 회귀 모델에서 다양한 관찰이 어떤 영향을 미치는지 알고 싶어하는 경우가 많습니다.

관측값의 영향을 계산하는 한 가지 방법은 DFBETAS 라는 측정항목을 사용하는 것입니다. 이는 각 개별 관측값을 제거하는 각 계수에 대한 표준화된 효과를 알려줍니다.

이 측정항목은 주어진 회귀 모델의 각 계수 추정치에 대한 각 관측값의 영향에 대한 아이디어를 제공합니다.

이 튜토리얼에서는 R 모델의 각 관측값에 대해 DFBETAS를 계산하고 시각화하는 방법에 대한 단계별 예를 보여줍니다.

1단계: 회귀 모델 만들기

먼저 R에 내장된 mtcars 데이터 세트를 사용하여 다중 선형 회귀 모델을 만듭니다.

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

2단계: 각 관찰에 대한 DFBETAS 계산

다음으로 내장된 dfbetas() 함수를 사용하여 모델의 각 관측값에 대한 DFBETAS 값을 계산합니다.

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

각 관측값에 대해 특정 관측값을 제거할 때 발생하는 원점, disp 변수 및 hp 변수에 대한 계수 추정치의 차이를 확인할 수 있습니다.

일반적으로 우리는 관측치가 2/ √n 의 임계값보다 큰 DBETAS 값을 갖는 경우 관측치가 주어진 계수의 추정에 강한 영향을 미친다고 간주합니다. 여기서 n 은 관측치 수입니다.

이 예에서 임계값은 0.3535534 입니다.

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

3단계: DFBETAS 시각화

마지막으로 모델의 각 관측값과 각 예측 변수에 대한 DFBETAS 값을 시각화하는 플롯을 만들 수 있습니다.

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

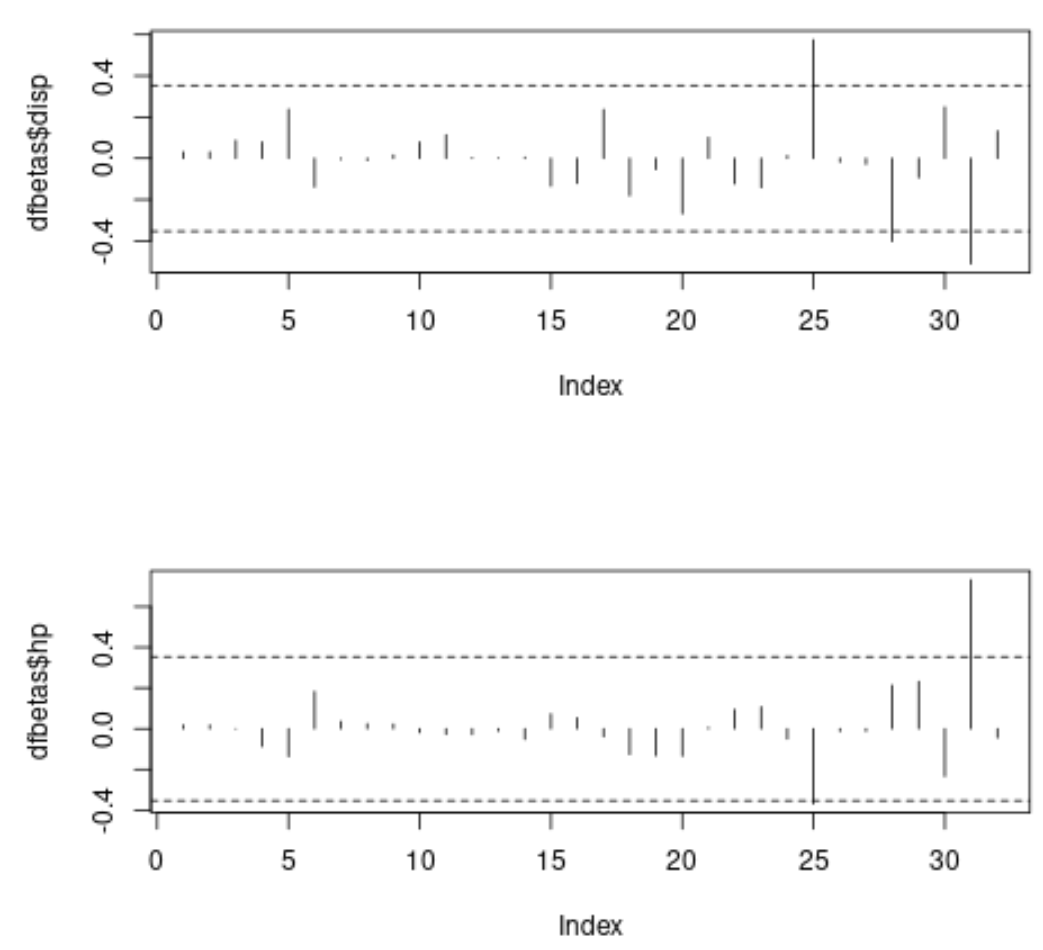
각 플롯에서 x축은 데이터 세트의 각 관측치에 대한 인덱스를 표시하고 y-값은 각 관측치 및 각 예측 변수에 해당하는 DFBETAS를 표시합니다.

첫 번째 플롯에서는 3개의 관측치가 절대 임계값 0.3535534 를 초과하는 것을 볼 수 있으며, 두 번째 플롯에서는 2개의 관측치가 절대 임계값을 초과하는 것을 볼 수 있습니다.

우리는 이러한 관찰을 더 자세히 연구하여 모델 계수 추정에 과도한 영향을 미치는지 여부를 결정할 수 있습니다.

추가 리소스

R에서 단순 선형 회귀를 수행하는 방법
R에서 다중 선형 회귀를 수행하는 방법
R에서 레버리지 통계를 계산하는 방법
R에서 DFFITS를 계산하는 방법