R에서 가중 최소 제곱 회귀를 수행하는 방법

선형 회귀 분석의 주요 가정 중 하나는 잔차가 예측 변수의 각 수준에서 등분산으로 분포된다는 것입니다. 이 가정을 등분산성(homoscedasticity) 이라고 합니다.

이 가정이 존중되지 않으면 잔차에 이분산성이 존재한다고 합니다. 이런 일이 발생하면 회귀 결과를 신뢰할 수 없게 됩니다.

이 문제를 해결하는 한 가지 방법은 가중치 최소 제곱 회귀를 사용하는 것입니다. 이는 오류 분산이 낮은 관측치 가 오류 분산이 큰 관측치에 비해 더 많은 정보를 포함하기 때문에 더 많은 가중치를 받도록 관측치에 가중치를 할당하는 것입니다.

이 튜토리얼에서는 R에서 가중치 최소 제곱 회귀를 수행하는 방법에 대한 단계별 예를 제공합니다.

1단계: 데이터 생성

다음 코드는 16명의 학생에 대한 학습 시간과 해당 시험 점수를 포함하는 데이터 프레임을 생성합니다.

 df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

2단계: 선형 회귀 수행

다음으로, lm() 함수를 사용하여 시간을 예측 변수로 사용하고 점수 를 응답 변수 로 사용하는 간단한 선형 회귀 모델을 피팅합니다.

 #fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-17,967 -5,970 -0.719 7,531 15,032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 60,467 5,128 11,791 1.17e-08 ***
hours 5,500 1,127 4,879 0.000244 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared: 0.6296, Adjusted R-squared: 0.6032 
F-statistic: 23.8 on 1 and 14 DF, p-value: 0.0002438

3단계: 이분산성 테스트

다음으로, 이분산성을 시각적으로 확인하기 위해 잔차와 적합치의 플롯을 만듭니다.

 #create residual vs. fitted plot
plot( fitted (model), resid (model), xlab=' Fitted Values ', ylab=' Residuals ')

#add a horizontal line at 0 
abline(0,0) 

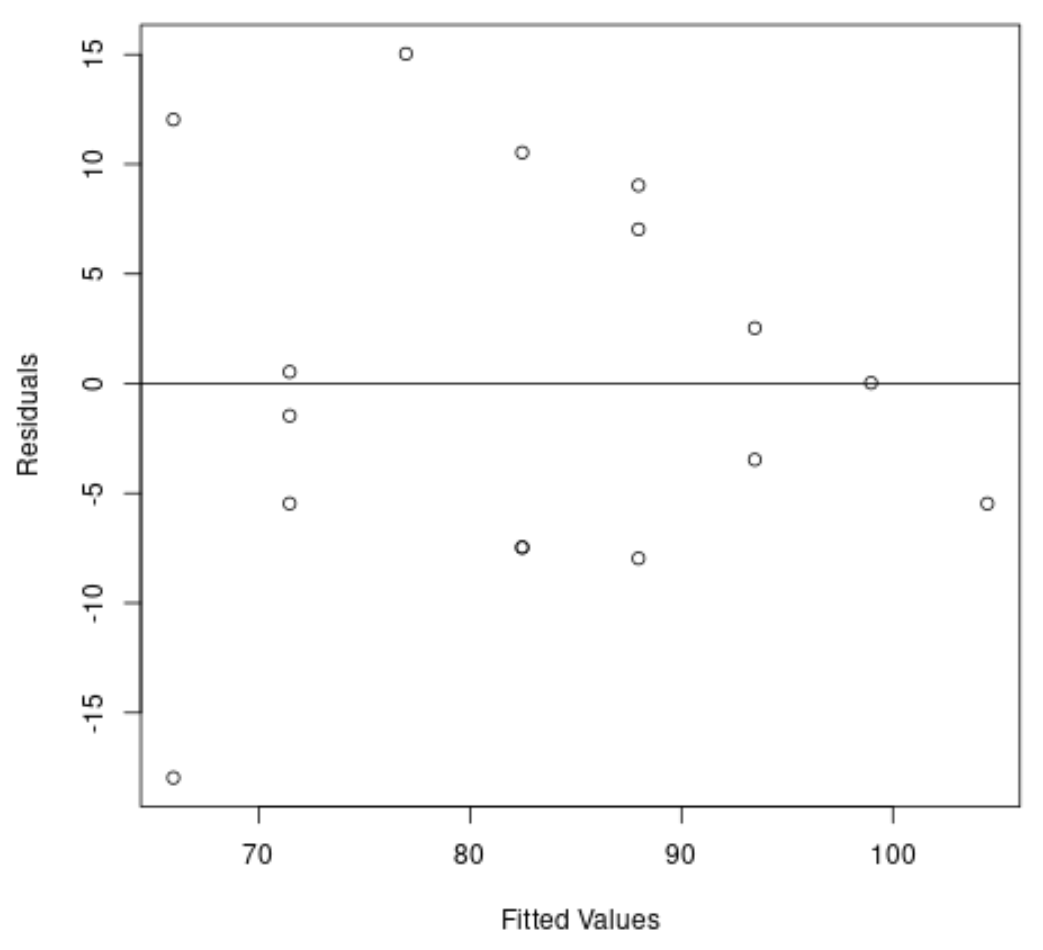
그래프에서 잔차가 “원뿔” 모양을 갖고 있음을 알 수 있습니다. 잔차는 그래프 전체에 등분산으로 분포되어 있지 않습니다.

이분산성을 공식적으로 테스트하기 위해 Breusch-Pagan 테스트를 수행할 수 있습니다.

 #load lmtest package
library (lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data: model
BP = 3.9597, df = 1, p-value = 0.0466

Breusch-Pagan 테스트는 다음과 같은 귀무 가설과 대립 가설을 사용합니다.

• 귀무 가설(H ₀ ): 등분산성이 존재합니다(잔차가 등분산으로 분포됨).
• 대립 가설( _HA ): 이분산성이 존재합니다(잔차가 등분산으로 분포되지 않음).

검정의 p-값이 0.0466 이므로 귀무 가설을 기각하고 이분산성이 이 모델에서 문제라는 결론을 내릴 것입니다.

4단계: 가중 최소 제곱 회귀 수행

이분산성이 존재하므로 분산이 낮은 관측치가 더 많은 가중치를 받도록 가중치를 설정하여 가중치 최소 제곱을 수행합니다.

 #define weights to use
wt <- 1 / lm( abs (model$residuals) ~ model$fitted. values )$fitted. values ^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min 1Q Median 3Q Max 
-2.0167 -0.9263 -0.2589 0.9873 1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.9689 5.1587 12.400 6.13e-09 ***
hours 4.7091 0.8709 5.407 9.24e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared: 0.6762, Adjusted R-squared: 0.6531 
F-statistic: 29.24 on 1 and 14 DF, p-value: 9.236e-05

결과에서 시간 예측 변수에 대한 계수 추정치가 약간 변경되고 전체 모델 적합도가 향상되었음을 알 수 있습니다.

가중 최소 제곱 모델의 잔차 표준 오차는 원래 단순 선형 회귀 모델의 9.224 와 비교하여 1.199 입니다.

이는 단순선형회귀모델로 생성한 예측값에 비해 가중최소제곱모델로 생성한 예측값이 실제 관측값에 훨씬 더 가깝다는 것을 의미합니다.

가중 최소 제곱 모델은 원래 단순 선형 회귀 모델의 0.6296 과 비교하여 R-제곱이 0.6762 입니다.

이는 가중 최소 제곱 모델이 단순 선형 회귀 모델보다 시험 점수의 변동을 더 많이 설명할 수 있음을 나타냅니다.

이러한 측정은 가중 최소 제곱 모델이 단순 선형 회귀 모델에 비해 데이터에 더 잘 맞는다는 것을 나타냅니다.

추가 리소스

R에서 단순 선형 회귀를 수행하는 방법
R에서 다중 선형 회귀를 수행하는 방법
R에서 분위수 회귀를 수행하는 방법