R에서 단순 선형 회귀를 수행하는 방법(단계별)

단순 선형 회귀는 단일 설명 변수 와 단일 응답 변수 간의 관계를 이해하는 데 사용할 수 있는 기술입니다.

간단히 말해서, 이 기술은 데이터에 가장 잘 맞는 선을 찾고 다음 형식을 취합니다.

ŷ = _b0 + _b1x

금:

• ŷ : 예상된 반응값
• b ₀ : 회귀선의 원점
• b ₁ : 회귀선의 기울기

이 방정식은 설명 변수와 응답 변수 사이의 관계를 이해하는 데 도움이 될 수 있으며 (통계적으로 유의하다고 가정하면) 설명 변수의 값이 주어진 경우 응답 변수의 값을 예측하는 데 사용할 수 있습니다.

이 튜토리얼에서는 R에서 간단한 선형 회귀를 수행하는 방법에 대한 단계별 설명을 제공합니다.

1단계: 데이터 로드

이 예에서는 15명의 학생에 대해 다음 두 가지 변수가 포함된 가짜 데이터 세트를 만듭니다.

• 특정 시험을 위해 공부한 총 시간
• 시험 결과

우리는 시간을 설명 변수로, 검사 결과를 반응 변수로 사용하여 단순 선형 회귀 모델을 맞추려고 시도할 것입니다.

다음 코드는 R에서 이 가짜 데이터 세트를 생성하는 방법을 보여줍니다.

 #create dataset
df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

#attach dataset to make it more convenient to work with
attach(df)

2단계: 데이터 시각화

단순 선형 회귀 모델을 피팅하기 전에 먼저 데이터를 시각화하여 이해해야 합니다.

첫째, 시간 과 점수 사이의 관계가 대략 선형인지 확인하려고 합니다. 이는 단순 선형 회귀의 대규모 기본 가정 이기 때문입니다. 두 변수 간의 관계를 시각화하기 위해 간단한 산점도를 만들 수 있습니다.

 scatter.smooth(hours, score, main=' Hours studied vs. Exam Score ')

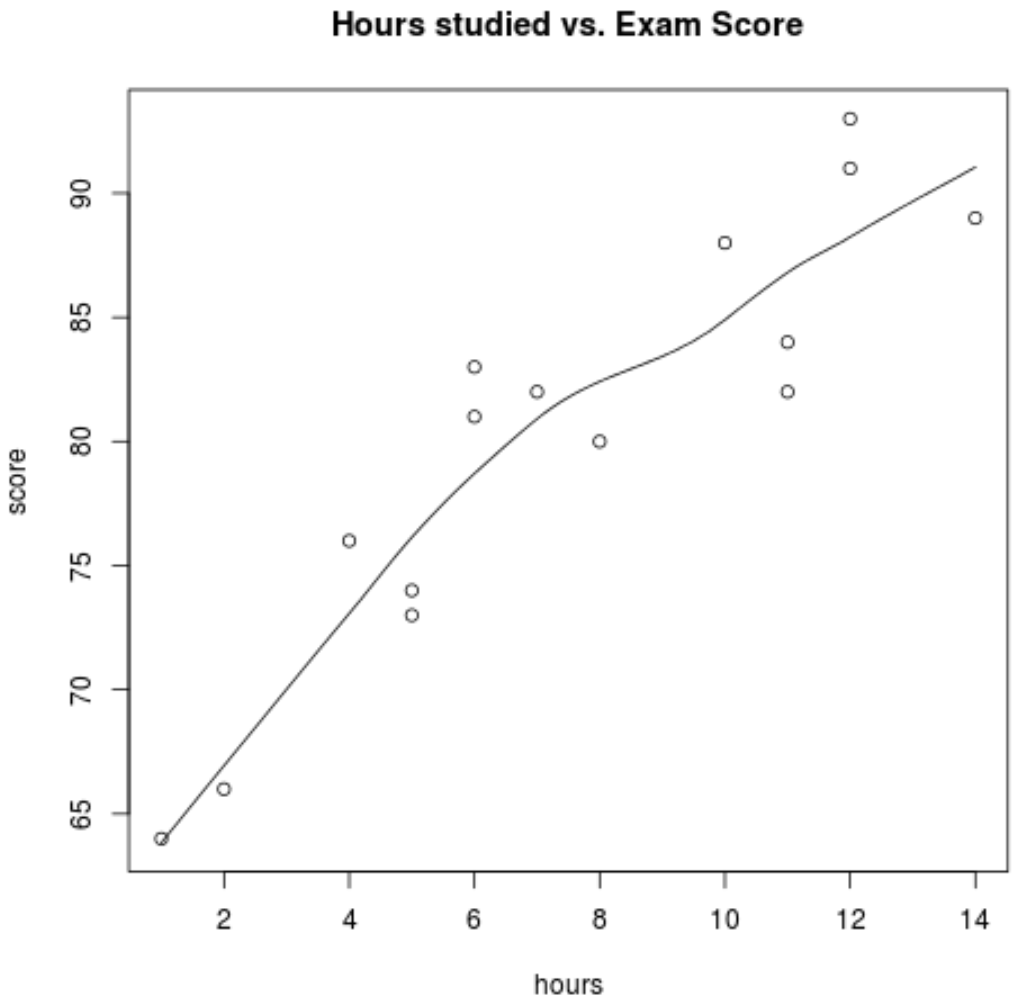
그래프를 보면 관계가 선형으로 나타나는 것을 볼 수 있습니다. 시간이 증가함에 따라 점수 도 선형적으로 증가하는 경향이 있습니다.

그런 다음 상자 그림을 만들어 시험 결과 분포를 시각화하고 이상값을 확인할 수 있습니다. 기본적으로 R은 관측치가 세 번째 사분위수(Q3) 위 사분위수 범위의 1.5배이거나 첫 번째 사분위수(Q1) 아래 사분위수 범위의 1.5배인 경우 관측치를 이상값으로 정의합니다.

관측치가 이상치인 경우 상자 그림에 작은 원이 나타납니다.

 boxplot(score) 

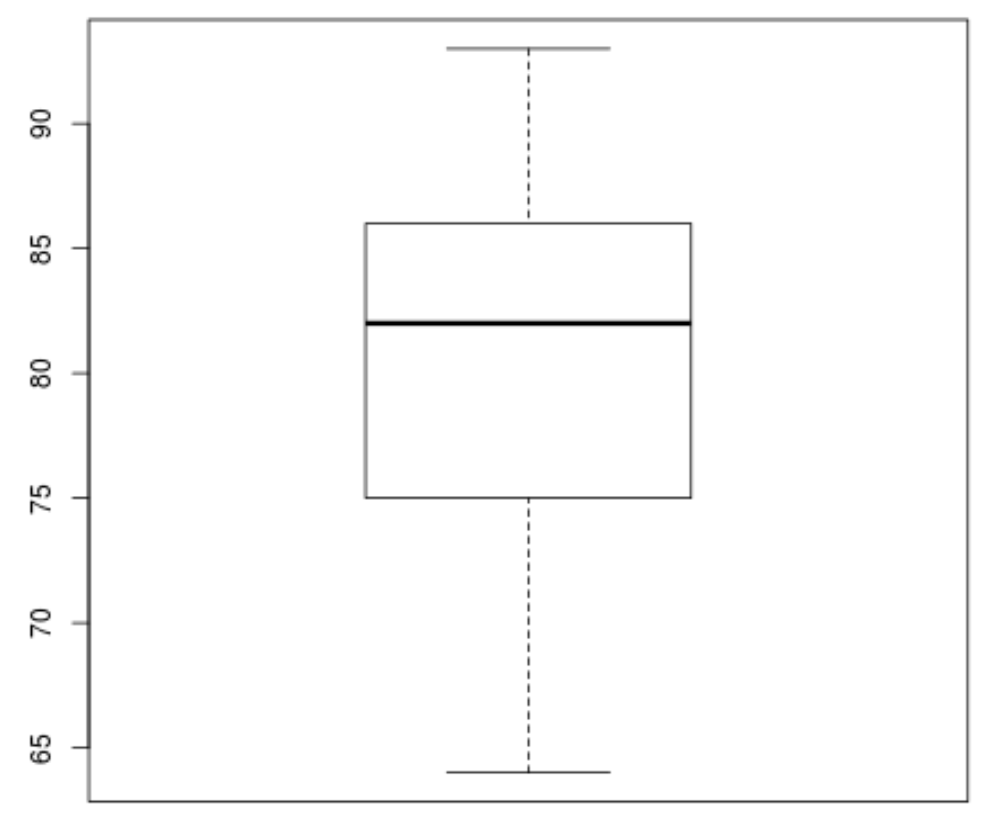
상자 그림에는 작은 원이 없습니다. 이는 데이터세트에 이상값이 없음을 의미합니다.

3단계: 단순 선형 회귀 수행

변수 간의 관계가 선형이고 이상값이 없음을 확인한 후에는 시간을 설명 변수로 사용하고 점수를 응답 변수로 사용하여 간단한 선형 회귀 모델을 적합화할 수 있습니다.

 #fit simple linear regression model
model <- lm(score~hours)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

모델 요약에서 적합 회귀 방정식은 다음과 같습니다.

점수 = 65.334 + 1.982*(시간)

이는 공부한 시간이 추가될 때마다 평균 시험 점수가 1,982 점 증가한다는 것을 의미합니다. 그리고 원래 값 65,334 는 0시간 공부하는 학생의 평균 예상 시험 점수를 알려줍니다.

또한 이 방정식을 사용하여 학생이 공부하는 시간을 기준으로 예상 시험 점수를 찾을 수도 있습니다. 예를 들어, 10시간 동안 공부한 학생은 시험 점수 85.15 를 달성해야 합니다.

점수 = 65.334 + 1.982*(10) = 85.15

모델 요약의 나머지 부분을 해석하는 방법은 다음과 같습니다.

• Pr(>|t|): 모델 계수와 연관된 p-값입니다. 시간 에 대한 p-값(2.25e-06)이 0.05보다 훨씬 작으므로 시간 과 점수 사이에 통계적으로 유의미한 연관성이 있다고 말할 수 있습니다.
• 다중 R-제곱: 이 숫자는 시험 점수의 변동 비율이 공부한 시간으로 설명될 수 있음을 나타냅니다. 일반적으로 회귀 모델의 R-제곱 값이 클수록 설명 변수가 응답 변수의 값을 더 잘 예측할 수 있습니다. 이 경우 점수 변동의 83.1%가 공부 시간으로 설명될 수 있습니다.
• 잔여 표준 오차: 관찰된 값과 회귀선 사이의 평균 거리입니다. 이 값이 낮을수록 회귀선이 관찰된 데이터와 더 많이 일치할 수 있습니다. 이 경우 시험에서 관찰된 평균 점수는 회귀선에서 예측한 점수와 3,641 점만큼 벗어납니다.
• F-통계량 및 p-값: F-통계량( 63.91 )과 해당 p-값( 2.253e-06 )은 회귀 모델의 전반적인 중요성, 즉 모델의 설명 변수가 변동을 설명하는 데 유용한지 여부를 알려줍니다. . 응답 변수에서. 이 예의 p-값은 0.05 미만이므로 모델이 통계적으로 유의미하며 시간은 점수 변화를 설명하는 데 유용한 것으로 간주됩니다.

4단계: 잔차 도표 생성

단순 선형 회귀 모델을 데이터에 맞춘 후 마지막 단계는 잔차 플롯을 만드는 것입니다.

선형 회귀 분석의 주요 가정 중 하나는 회귀 모델의 잔차가 대략 정규 분포를 따르고 설명 변수의 각 수준에서 등분산적 이라는 것입니다. 이러한 가정이 충족되지 않으면 회귀 모델의 결과가 오해의 소지가 있거나 신뢰할 수 없을 수 있습니다.

이러한 가정이 충족되는지 확인하기 위해 다음과 같은 잔차 그림을 만들 수 있습니다.

잔차 대 적합치 도표: 이 도표는 등분산성을 확인하는 데 유용합니다. x축은 적합치를 표시하고 y축은 잔차를 표시합니다. 잔차가 0 값을 중심으로 그래프 전체에 무작위로 균일하게 분포되어 있는 것처럼 보이는 한 등분산성이 위반되지 않는다고 가정할 수 있습니다.

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

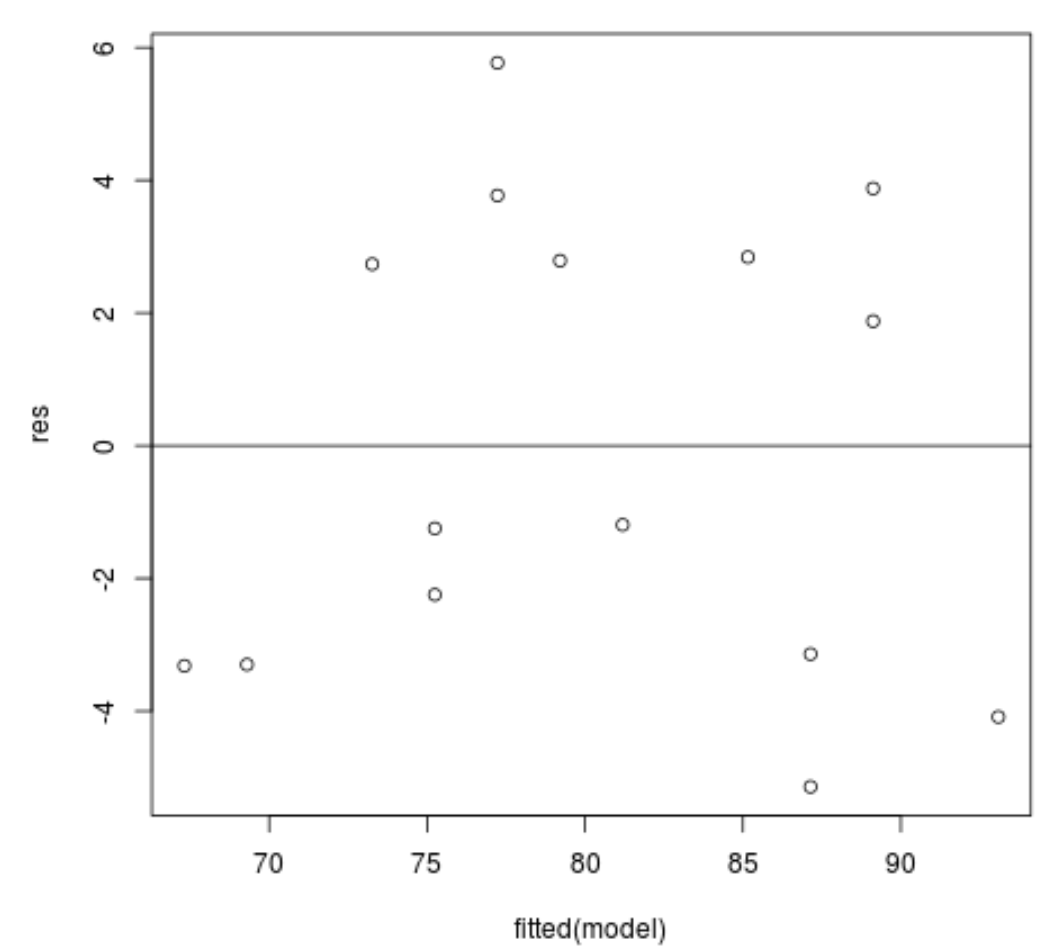
잔차는 0 주위에 무작위로 흩어져 있는 것처럼 보이고 눈에 띄는 패턴을 나타내지 않으므로 이 가정이 충족됩니다.

QQ 플롯: 이 플롯은 잔차가 정규 분포를 따르는지 여부를 결정하는 데 유용합니다. 플롯의 데이터 값이 대략 45도 각도의 직선을 따르는 경우 데이터는 정규 분포를 따릅니다.

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

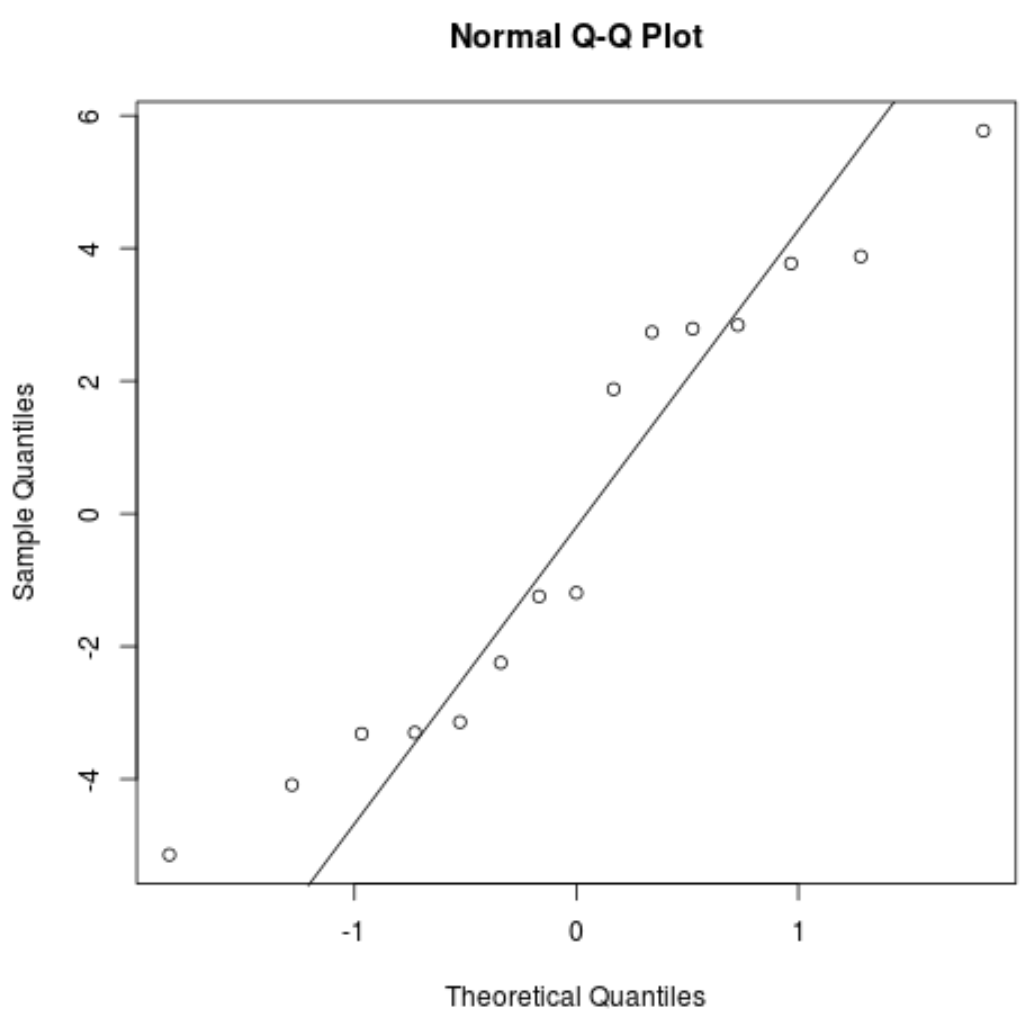
잔차는 45도 선에서 약간 벗어나 있지만 심각한 우려를 불러일으킬 정도는 아닙니다. 정규성 가정이 충족된다고 가정할 수 있다.

잔차는 정규분포 및 등분산성을 나타내므로 단순선형회귀모형의 가정이 만족됨을 확인하였다. 따라서 우리 모델의 출력은 신뢰할 수 있습니다.

이 튜토리얼에 사용된 전체 R 코드는 여기에서 찾을 수 있습니다.