R의 부분 최소 제곱(단계별)
기계 학습에서 직면하게 되는 가장 일반적인 문제 중 하나는 다중 공선성 입니다. 이는 데이터 세트에서 두 개 이상의 예측 변수가 높은 상관 관계를 가질 때 발생합니다.
이런 일이 발생하면 모델은 훈련 데이터 세트에 잘 맞을 수 있지만, 훈련 데이터 세트에 과적합되기 때문에 본 적이 없는 새로운 데이터 세트에서는 성능이 저하 될 수 있습니다. 트레이닝 세트.
이 문제를 해결하는 한 가지 방법은 다음과 같이 작동하는 부분 최소 제곱 법을 사용하는 것입니다.
- 예측 변수와 반응 변수를 표준화합니다.
- 반응 변수와 예측 변수 모두에서 상당한 양의 변동을 설명하는 p개의 원래 예측 변수 의 M개의 선형 조합(“PLS 구성 요소”라고 함)을 계산합니다 .
- PLS 구성요소를 예측 변수로 사용하여 선형 회귀 모델을 맞추려면 최소 제곱법을 사용합니다.
- k-겹 교차 검증을 사용하여 모델에 유지할 최적의 PLS 구성 요소 수를 찾습니다.
이 튜토리얼에서는 R에서 부분 최소 제곱을 수행하는 방법에 대한 단계별 예를 제공합니다.
1단계: 필요한 패키지 로드
R에서 부분 최소 제곱을 수행하는 가장 쉬운 방법은 pls 패키지의 함수를 사용하는 것입니다.
#install pls package (if not already installed) install.packages(" pls ") load pls package library(pls)
2단계: 부분 최소 제곱 모델 피팅
이 예에서는 다양한 유형의 자동차에 대한 데이터가 포함된 mtcars 라는 내장 R 데이터 세트를 사용합니다.
#view first six rows of mtcars dataset
head(mtcars)
mpg cyl disp hp drat wt qsec vs am gear carb
Mazda RX4 21.0 6 160 110 3.90 2.620 16.46 0 1 4 4
Mazda RX4 Wag 21.0 6 160 110 3.90 2.875 17.02 0 1 4 4
Datsun 710 22.8 4 108 93 3.85 2.320 18.61 1 1 4 1
Hornet 4 Drive 21.4 6 258 110 3.08 3.215 19.44 1 0 3 1
Hornet Sportabout 18.7 8 360 175 3.15 3.440 17.02 0 0 3 2
Valiant 18.1 6 225 105 2.76 3,460 20.22 1 0 3 1
이 예에서는 hp를 응답 변수 로 사용하고 다음 변수를 예측 변수로 사용하여 부분 최소 제곱(PLS) 모델을 적합합니다.
- mpg
- 표시하다
- 똥
- 무게
- q초
다음 코드는 PLS 모델을 이 데이터에 맞추는 방법을 보여줍니다. 다음 인수에 유의하세요.
- scale=TRUE : 이는 데이터 세트의 각 변수가 평균 0, 표준 편차 1을 갖도록 스케일링되어야 함을 R에 알려줍니다. 이렇게 하면 다른 단위로 측정할 경우 예측 변수가 모델에 너무 많은 영향을 미치지 않도록 합니다.
- 검증=”CV” : R에게 k-겹 교차 검증을 사용하여 모델 성능을 평가하도록 지시합니다. 이는 기본적으로 k=10 접기를 사용한다는 점에 유의하세요. 또한 Leave-One-Out 교차 검증을 수행하는 대신 “LOOCV”를 지정할 수도 있습니다.
#make this example reproducible set.seed(1) #fit PCR model model <- plsr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale= TRUE , validation=" CV ")
3단계: PLS 구성 요소 수 선택
모델을 피팅한 후에는 유지할 PLS 구성 요소 수를 결정해야 합니다.
이를 수행하려면 k-교차 검증으로 계산된 테스트 평균 제곱근 오차(테스트 RMSE)를 살펴보세요.
#view summary of model fitting
summary(model)
Data:
Y dimension: 32 1
Fit method: kernelpls
Number of components considered: 5
VALIDATION: RMSEP
Cross-validated using 10 random segments.
(Intercept) 1 comp 2 comps 3 comps 4 comps 5 comps
CV 69.66 40.57 35.48 36.22 36.74 36.67
adjCV 69.66 40.41 35.12 35.80 36.27 36.20
TRAINING: % variance explained
1 comp 2 comps 3 comps 4 comps 5 comps
X 68.66 89.27 95.82 97.94 100.00
hp 71.84 81.74 82.00 82.02 82.03
결과에는 두 가지 흥미로운 테이블이 있습니다.
1. 검증: RMSEP
이 표는 k-겹 교차 검증으로 계산된 RMSE 테스트를 보여줍니다. 우리는 다음을 볼 수 있습니다:
- 모델에서 원래 항만 사용하는 경우 테스트의 RMSE는 69.66 입니다.
- 첫 번째 PLS 구성 요소를 추가하면 RMSE 테스트는 40.57로 떨어집니다.
- 두 번째 PLS 구성 요소를 추가하면 RMSE 테스트는 35.48로 떨어집니다.
PLS 구성 요소를 추가하면 실제로 테스트의 RMSE가 증가하는 것을 볼 수 있습니다. 따라서 최종 모델에서는 두 개의 PLS 구성 요소만 사용하는 것이 최적인 것으로 보입니다.
2. 훈련: 설명된 분산 %
이 표는 PLS 구성요소에 의해 설명되는 반응 변수의 분산 비율을 보여줍니다. 우리는 다음을 볼 수 있습니다:
- 첫 번째 PLS 성분만 사용하여 응답 변수 변동의 68.66% 를 설명할 수 있습니다.
- 두 번째 PLS 성분을 추가하면 응답 변수의 변동의 89.27% 를 설명할 수 있습니다.
더 많은 PLS 구성요소를 사용하여 더 많은 분산을 설명할 수 있지만, 두 개 이상의 PLS 구성요소를 추가해도 실제로 설명되는 분산의 비율이 증가하지 않는다는 것을 알 수 있습니다.
또한 검증 플롯() 함수를 사용하여 RMSE 테스트(MSE 및 R-제곱 테스트와 함께)를 PLS 구성 요소 수의 함수로 시각화할 수 있습니다.
#visualize cross-validation plots validationplot(model) validationplot(model, val.type=" MSEP ") validationplot(model, val.type=" R2 ")
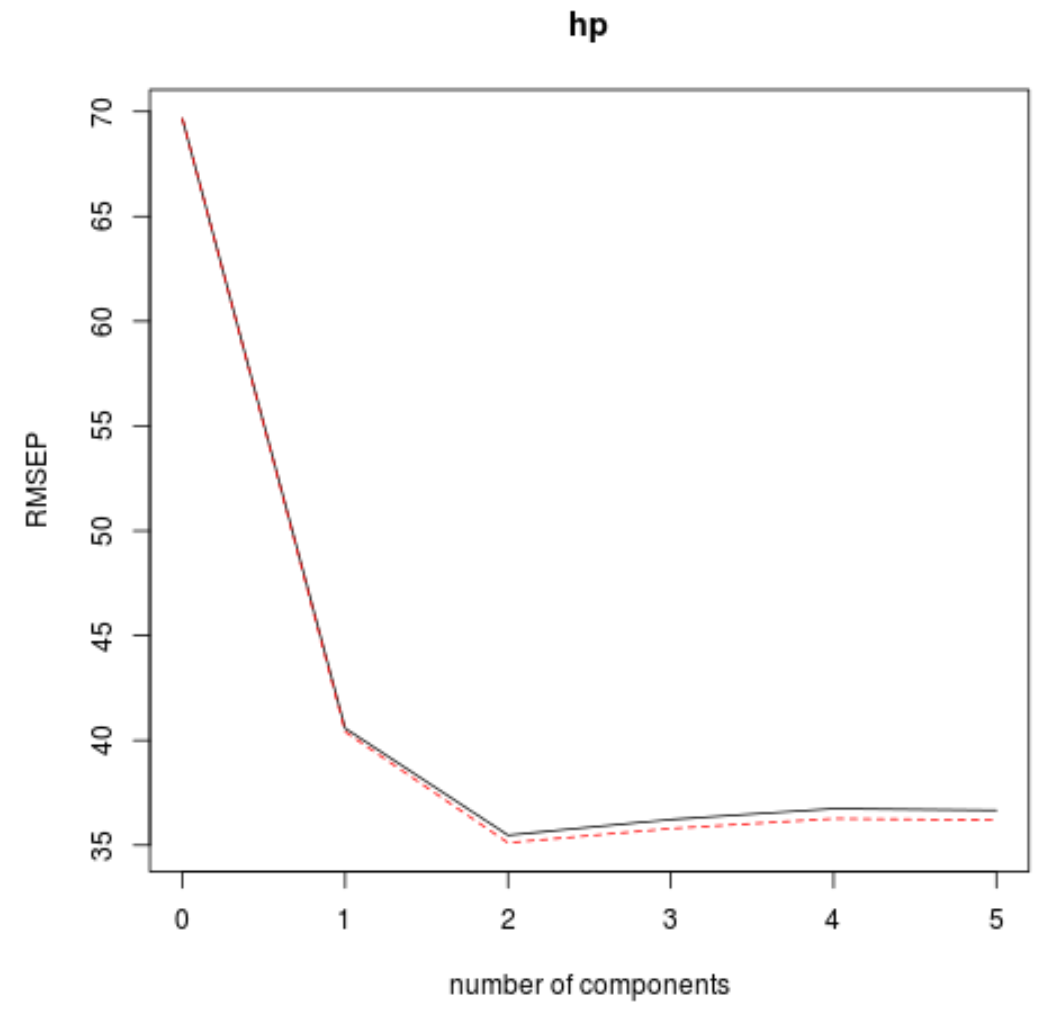
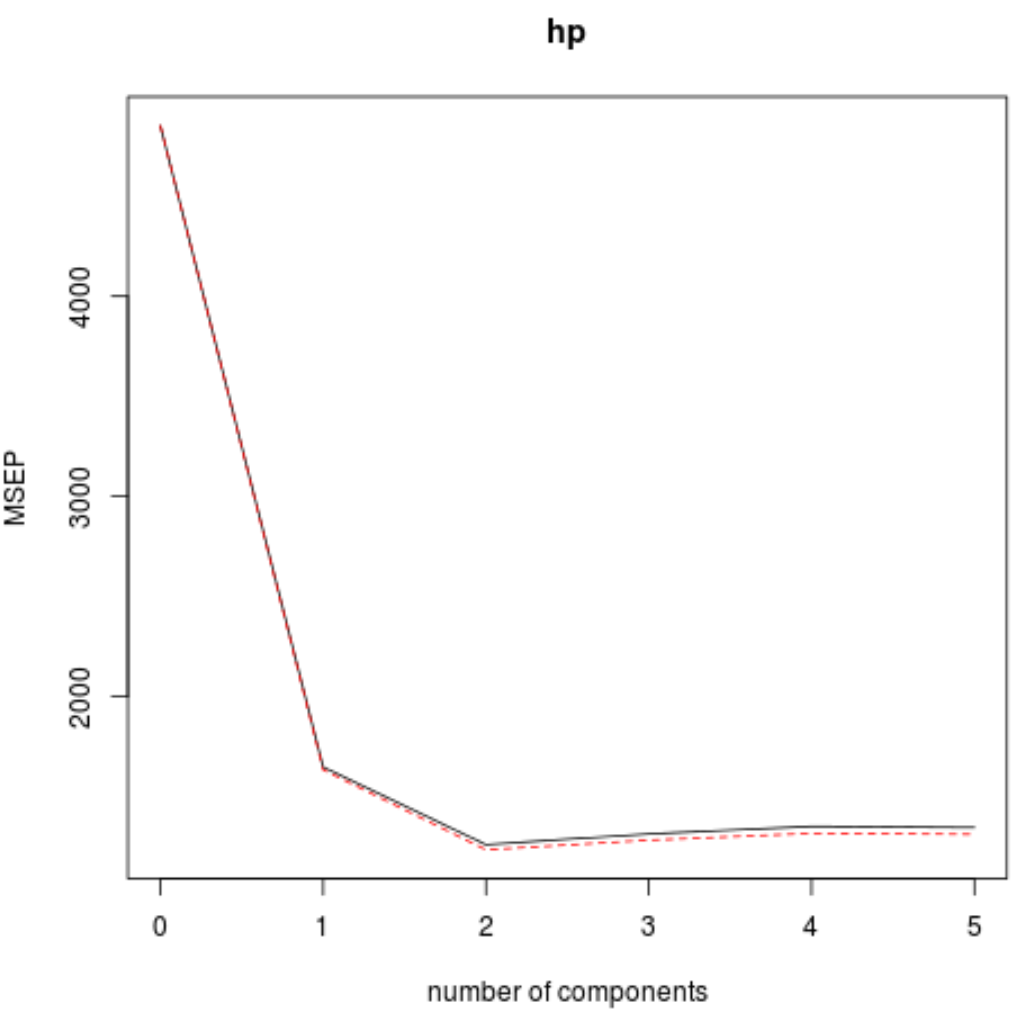
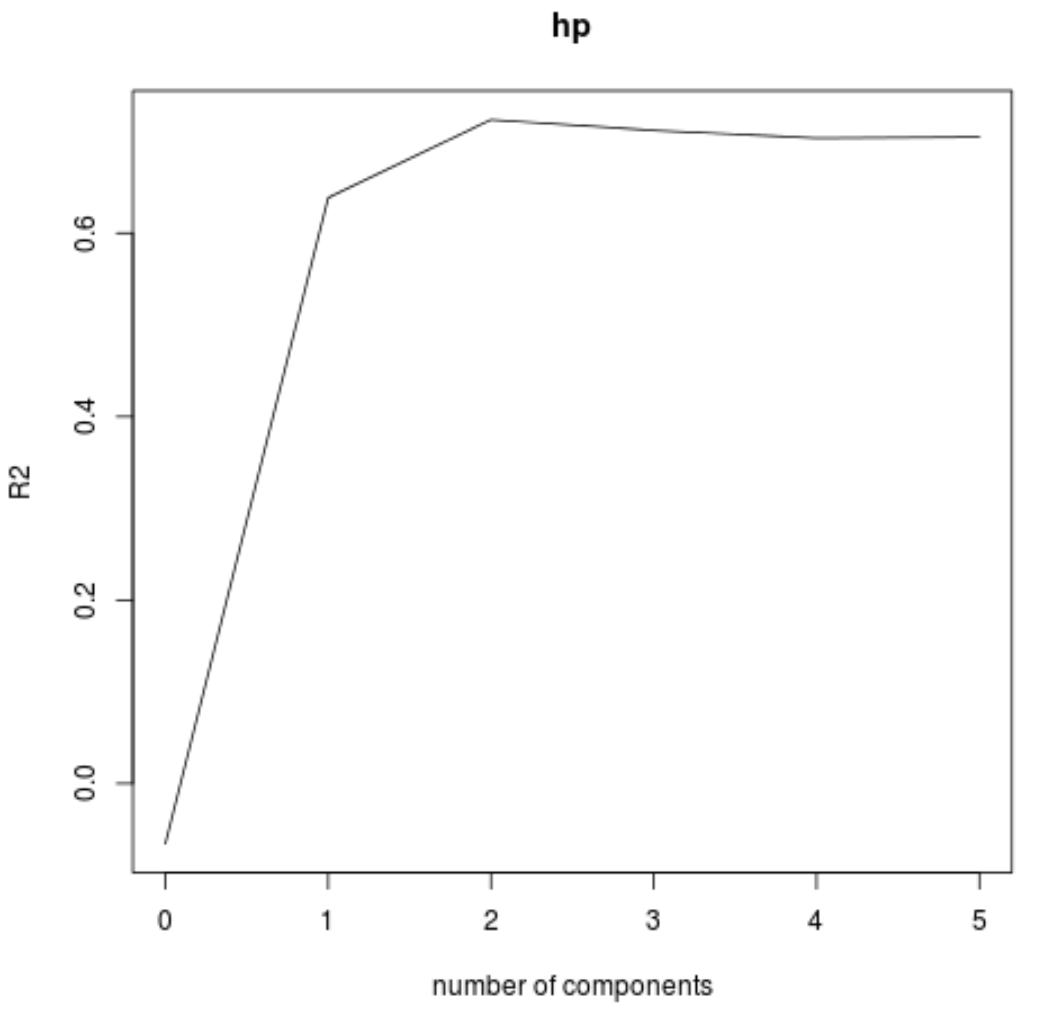
각 그래프에서 두 개의 PLS 구성 요소를 추가하면 모델 적합도가 향상되지만 PLS 구성 요소를 더 추가하면 모델 적합도가 저하되는 경향이 있음을 알 수 있습니다.
따라서 최적의 모델에는 처음 두 개의 PLS 구성 요소만 포함됩니다.
4단계: 최종 모델을 사용하여 예측
두 개의 PLS 구성요소가 포함된 최종 모델을 사용하여 새로운 관측값에 대해 예측할 수 있습니다.
다음 코드는 원본 데이터세트를 훈련 세트와 테스트 세트로 분할하고 두 개의 PLS 구성요소가 있는 최종 모델을 사용하여 테스트 세트에 대해 예측하는 방법을 보여줍니다.
#define training and testing sets train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")] y_test <- mtcars[26: nrow (mtcars), c("hp")] test <- mtcars[26: nrow (mtcars), c("mpg", "disp", "drat", "wt", "qsec")] #use model to make predictions on a test set model <- plsr(hp~mpg+disp+drat+wt+qsec, data=train, scale= TRUE , validation=" CV ") pcr_pred <- predict(model, test, ncomp= 2 ) #calculate RMSE sqrt ( mean ((pcr_pred - y_test)^2)) [1] 54.89609
테스트의 RMSE는 54.89609 로 나타났습니다. 이는 테스트 세트 관찰에 대해 예측된 HP 값과 관찰된 HP 값 사이의 평균 편차입니다.
두 개의 주성분이 포함된 등가 주성분 회귀 모델은 56.86549 의 테스트 RMSE를 생성했습니다. 따라서 PLS 모델은 이 데이터세트에 대해 PCR 모델보다 약간 더 나은 성능을 보였습니다.
이 예제에서 R 코드의 전체 사용법은 여기에서 확인할 수 있습니다.