Sas에서 이상값을 식별하는 방법(예제 포함)

이상값 은 데이터 세트의 다른 값과 비정상적으로 멀리 떨어져 있는 관측값입니다. 이상값은 분석 결과에 영향을 미칠 수 있으므로 문제가 될 수 있습니다.

데이터 세트에서 이상값을 식별하는 가장 일반적인 방법은 사분위간 범위를 사용하는 것입니다.

IQR(사분위수 범위)은 데이터 세트에서 75번째 백분위수(Q3)와 25번째 백분위수(Q1) 간의 차이입니다. 평균 50% 값의 분포를 측정합니다.

일반적으로 관측값이 세 번째 사분위수(Q3) 위 사분위수 범위의 1.5배이거나 첫 번째 사분위수(Q1) 아래 사분위수 범위의 1.5배인 경우 관측치를 이상치로 정의합니다.

특이치 = 관측치 > Q3 + 1.5*IQR 또는 < Q1 – 1.5*IQR

다음 예에서는 이 공식을 사용하여 SAS의 데이터 세트에서 이상값을 식별하는 방법을 보여줍니다.

예: SAS에서 이상값 식별

SAS에 다음과 같은 데이터 세트가 있다고 가정해 보겠습니다.

 /*create dataset*/
data original_data;
    input team $points;
    datalines ;
At 18
B24
C26
D 34
E 38
F45
G 48
H 54
I 60
Day 73
K 79
L 85
M 94
No. 98
O 221
P 223
;
run ;

/*view dataset*/
proc print data = original_data;

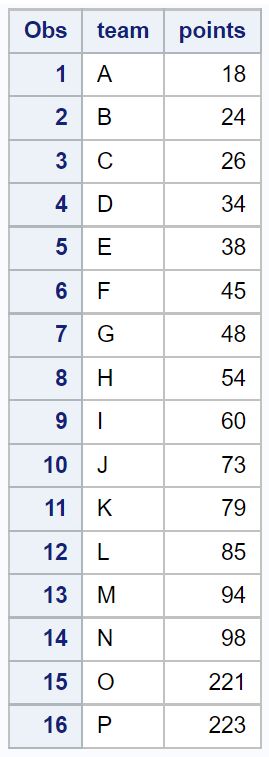
SAS에서 이상값을 식별하는 가장 쉬운 방법은 앞서 언급한 공식을 자동으로 사용하여 데이터세트의 이상값을 작은 원으로 식별하고 표시하는 상자 그림을 만드는 것입니다.

 /*create boxplot to visualize distribution of points*/
ods output sgplot=boxplot_data;
proc sgplot data =original_data;
    vbox points;
run ;

/*view summary of boxplot descriptive statistics*/
proc print data =boxplot_data; 

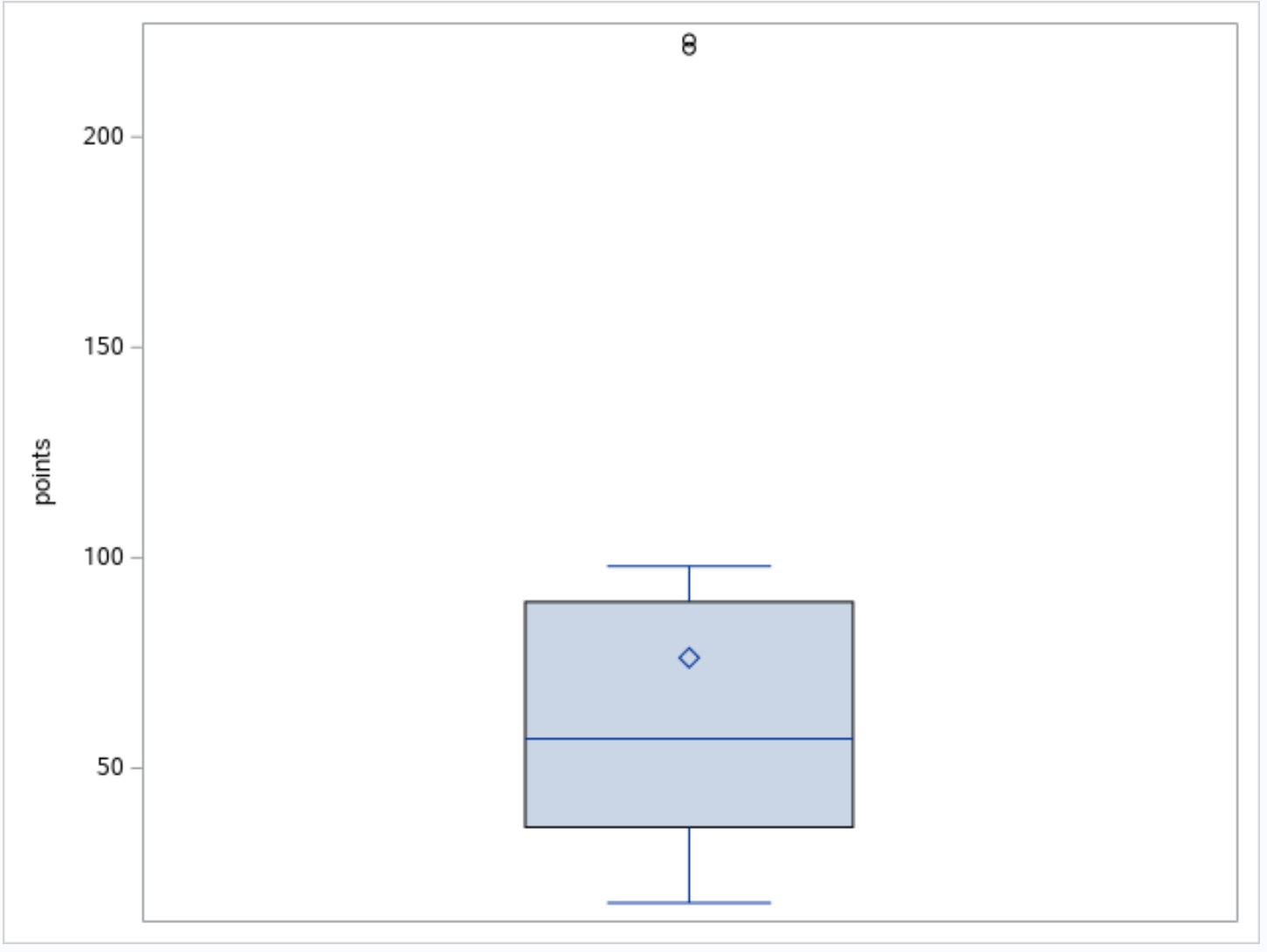
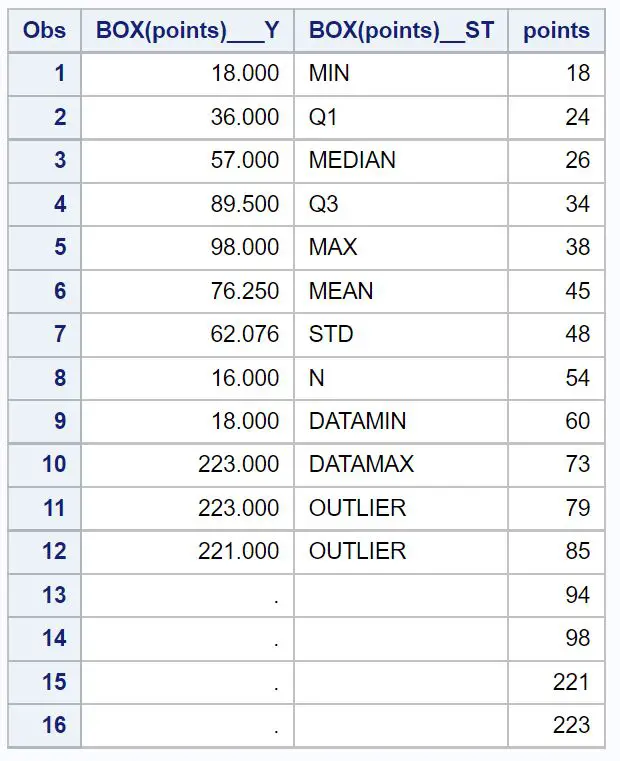
상자 그림에서 그림 상단 근처에 두 개의 작은 원이 있음을 알 수 있습니다. 이는 두 개의 이상값이 있음을 나타냅니다.

상자 그림 아래 표에서 두 가지 이상치인 221 과 223 의 정확한 값을 볼 수 있습니다.

이전 공식을 사용하여 이 두 값이 이상값인지 수동으로 확인할 수 있습니다.

특이치 = 관측치 > Q3 + 1.5*IQR 또는 < Q1 – 1.5*IQR

사분위간 범위는 Q3 – Q1 = 89.5 – 36 = 53.5입니다.

이상값의 상한은 Q3 + 1.5*IQR = 89.5 + 1.5*53.5 = 169.75입니다.

221 과 223은 모두 이 값보다 크므로 이상값으로 분류됩니다.

그런 다음 원하는 경우 다음 코드를 사용하여 데이터 세트에서 이러한 두 가지 이상값을 제거할 수 있습니다.

 /*create new dataset with outliers removed*/
data new_data;
    set original_data;
    if points >= 221 then delete;
run ;

/*view new dataset*/
proc print data =new_data; 

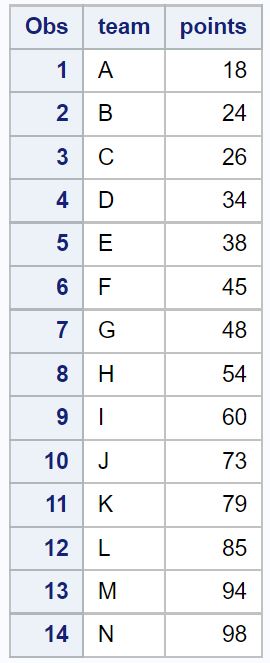
두 개의 이상값이 제거되었습니다.

추가 리소스

다음 튜토리얼에서는 SAS에서 다른 일반적인 작업을 수행하는 방법을 설명합니다.

SAS에서 절차 요약을 사용하는 방법
SAS에서 Proc Tabulate를 사용하는 방법
SAS에서 상관관계를 계산하는 방법
SAS에서 빈도표를 만드는 방법
SAS에서 누락된 값을 0으로 바꾸는 방법