스네데코 f 유통
이 기사에서는 Snedecor F 배포판이 무엇인지, 그리고 어떤 용도로 사용되는지 설명합니다. 또한 Snedecor F 분포 그래프와 그 통계적 속성이 무엇인지 확인할 수 있습니다.
Snedecor F 분포란 무엇입니까?
피셔-스네데코 F 분포 또는 간단히 F 분포 라고도 하는 스네데코 F 분포는 통계적 추론, 특히 분산 분석에 사용되는 연속 확률 분포입니다.
Snedecor F 분포의 속성 중 하나는 자유도를 나타내는 두 개의 실수 매개변수 m 및 n 값으로 정의된다는 것입니다. 따라서 Snedecor 분포 F의 기호는 F m,n 입니다. 여기서 m 과 n 은 분포를 정의하는 매개변수입니다.

![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
Fisher-Snedecor F 분포는 영국 통계학자 Ronald Fisher와 미국 통계학자 George Snedecor의 이름을 따서 명명되었습니다.
통계에서 Fisher-Snedecor F 분포는 다양한 용도로 사용됩니다. 예를 들어, Fisher-Snedecor F 분포는 다양한 선형 회귀 모델을 비교하는 데 사용되며 이 확률 분포는 분산 분석(ANOVA)에 사용됩니다.
Snedor F 분포도
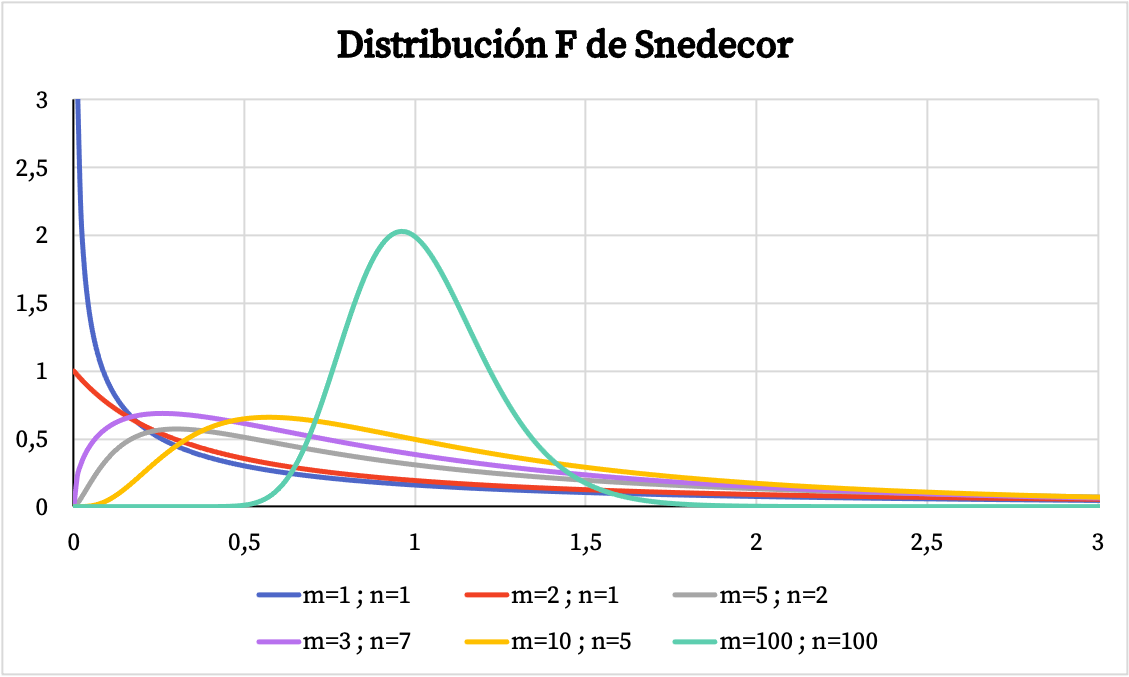
Snedecor F 분포의 정의를 확인한 후 밀도 함수 그래프와 누적 확률 그래프가 아래에 표시됩니다.
아래 그래프에서는 자유도가 서로 다른 Snedecor F 분포의 여러 예를 볼 수 있습니다.
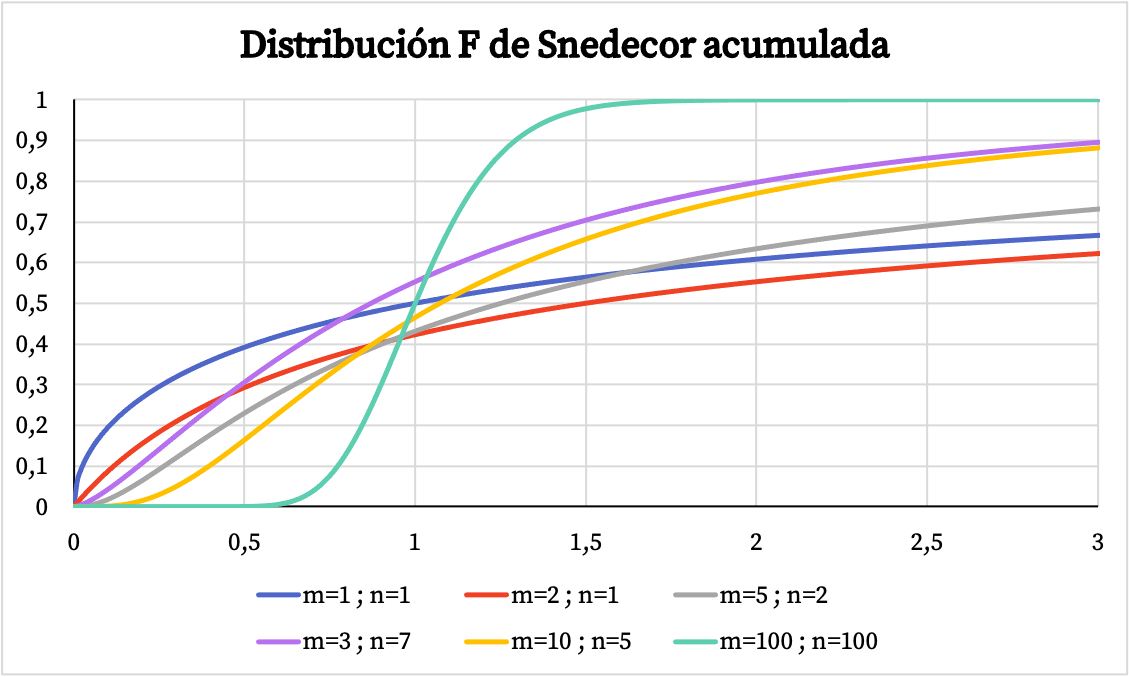
한편, 아래 그래프를 보면 Snedecor F 분포의 누적확률함수 그래프가 특성값에 따라 어떻게 변화하는지 확인할 수 있습니다.
Snedecor F 분포의 특성
마지막으로 이 섹션에서는 Snedecor F 분포의 가장 중요한 특성을 제시합니다.
- Snedecor F 분포의 자유도 m 과 n은 분포의 모양을 정의하는 두 개의 매개변수입니다. Snedecor F 분포의 이러한 특성 값은 양의 정수입니다.
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> Snedecor F 분포의 영역은 0보다 크거나 같은 모든 실수로 구성됩니다.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- 2 보다 큰 n 값의 경우 Snedecor F 분포의 평균은 n 에서 2를 뺀 값과 같습니다.
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> 매개변수 <em>n</em> 이 2보다 큰 경우 Snedecor 분포 F의 분산은 다음 공식을 적용하여 계산할 수 있습니다.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p>
</p>
<ul>
<li> 매개변수 <em>m이</em> 2보다 큰 경우 Snedecor 분포 F의 최빈값은 다음 식으로 계산할 수 있습니다.</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
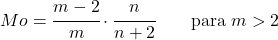
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- 변수가 자유도가 m 및 n 인 Snedecor F 분포를 따르는 경우, 해당 변수의 역은 자유도가 동일하지만 값의 순서가 변경되는 Snedecor F 분포를 따릅니다.
![]()
- 학생 분포는 Snedecor F 분포와 다음과 같은 관계를 갖습니다.
![]()