Spss에서 로지스틱 회귀를 수행하는 방법

로지스틱 회귀는 응답 변수가 이진일 때 회귀 모델을 맞추는 데 사용하는 방법입니다.

이 튜토리얼에서는 SPSS에서 로지스틱 회귀를 수행하는 방법을 설명합니다.

예: SPSS의 로지스틱 회귀

다음 단계를 사용하여 대학 농구 선수가 GPA를 기반으로 NBA에 드래프트되었는지 여부(초안: 0 = 아니요, 1 = 예)를 나타내는 데이터 세트에 대해 SPSS에서 로지스틱 회귀를 수행합니다. 게임당 포인트 및 디비전 레벨.

1단계: 데이터를 입력합니다.

먼저 다음 데이터를 입력합니다.

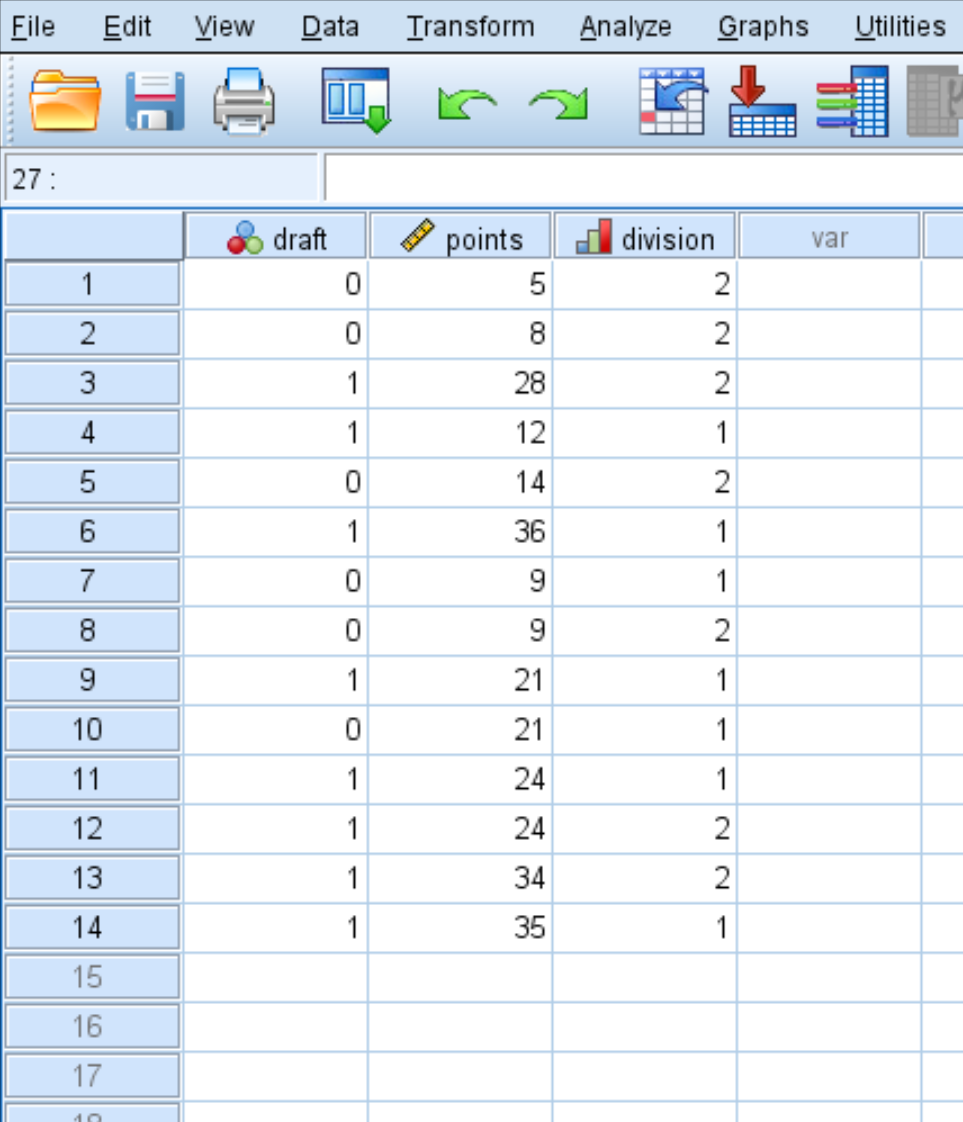
2단계: 로지스틱 회귀를 수행합니다.

분석 탭, 회귀 , 이진 로지스틱 회귀를 차례로 클릭합니다.

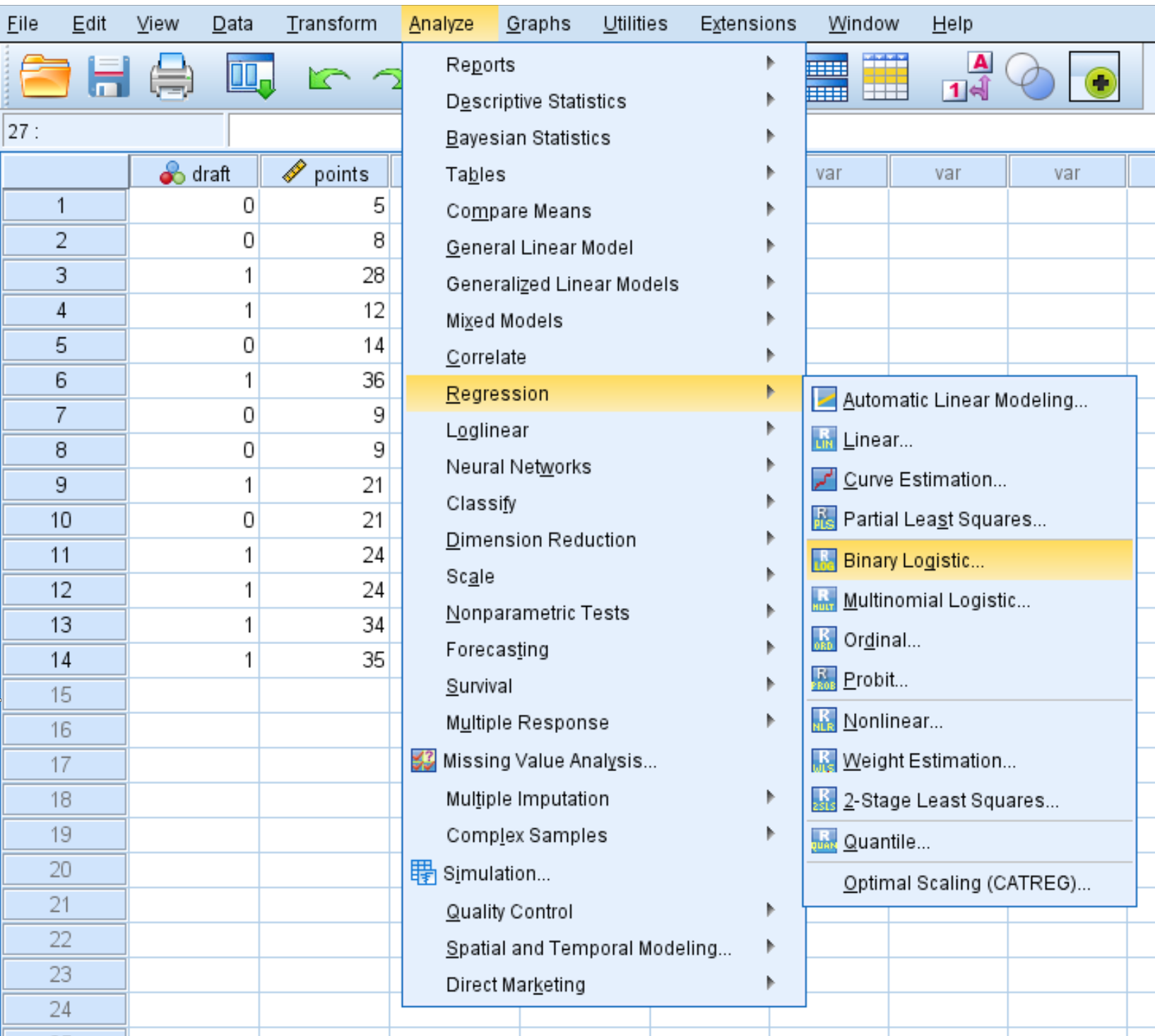
나타나는 새 창에서 이항 반응 변수 프로젝트를 종속이라고 표시된 영역으로 끌어 놓습니다. 그런 다음 예측 변수의 콜론 과 나눗셈을 Block 1 of 1이라고 표시된 상자로 드래그합니다. 방법을 Enter로 설정된 상태로 둡니다. 그런 다음 확인을 클릭합니다.

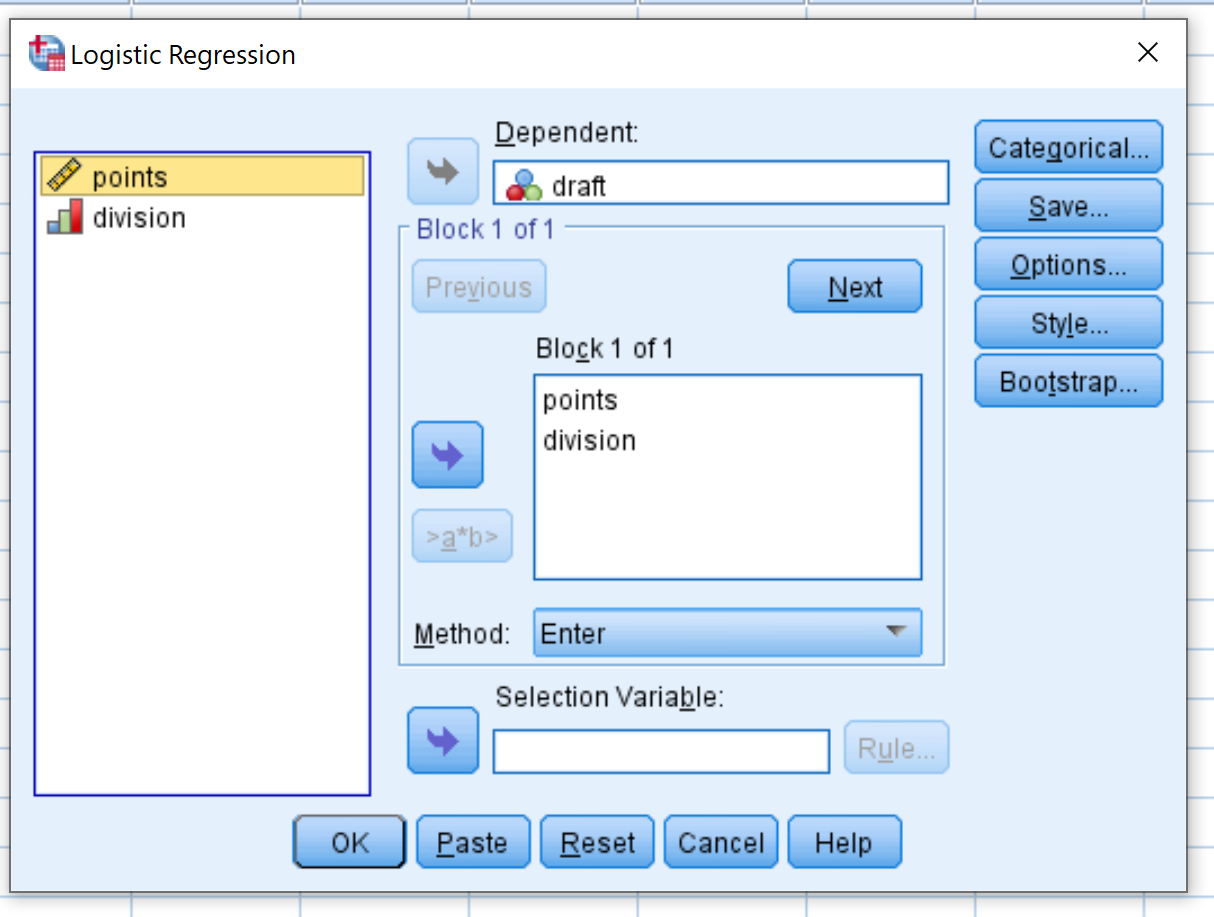
3단계. 결과를 해석합니다.

확인을 클릭하면 로지스틱 회귀 결과가 나타납니다.

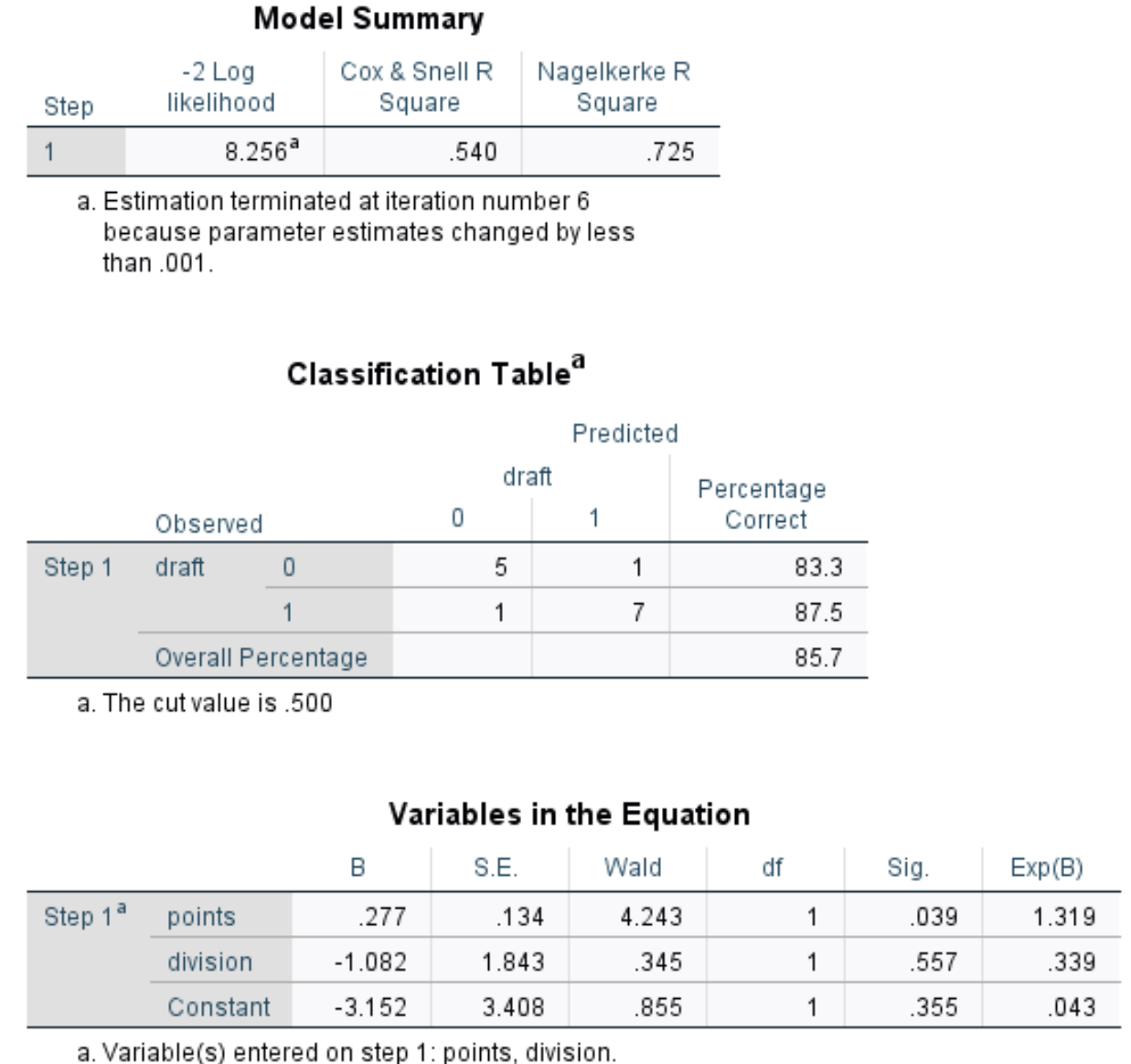
결과를 해석하는 방법은 다음과 같습니다.

모델 요약: 이 표에서 가장 유용한 측정항목은 예측 변수로 설명할 수 있는 반응 변수 의 변동 비율을 알려주는 Nagelkerke R Square입니다. 이 경우 점과 구분은 초안 변동성의 72.5% 를 설명할 수 있습니다.

분류 테이블: 이 테이블에서 가장 유용한 측정항목은 모델이 올바르게 분류할 수 있는 관측치의 비율을 알려주는 전체 비율입니다. 이 경우 로지스틱 회귀 모델은 85.7% 의 선수의 드래프트 결과를 정확하게 예측할 수 있었습니다.

방정식의 변수: 이 마지막 표는 다음을 포함하여 몇 가지 유용한 측정값을 제공합니다.

• Wald: 각 예측 변수에 대한 Wald 검정 통계량으로, 각 예측 변수가 통계적으로 유의한지 여부를 확인하는 데 사용됩니다.
• Sig: 각 예측 변수에 대한 Wald 검정 통계량에 해당하는 p-값입니다. 점 에 대한 p-값은 0.039이고 나누기에 대한 p-값은 0.557임을 알 수 있습니다.
• Exp(B): 각 예측 변수에 대한 승산비입니다. 이는 주어진 예측 변수의 1단위 증가와 관련된 선수 드래프트 확률의 변화를 알려줍니다. 예를 들어 Division 2 선수가 드래프트될 확률은 Division 1 선수가 드래프트될 확률의 0.339에 불과합니다. 마찬가지로, 게임당 포인트가 추가로 한 단위 증가할 때마다 선수가 드래프트될 확률이 1,319씩 증가합니다.

그런 다음 계수(B로 표시된 열의 값)를 사용하여 다음 공식을 사용하여 특정 선수가 드래프트될 확률을 예측할 수 있습니다.

확률 = e ^{-3.152 + 0.277(점) – 1.082(나눗셈)} / (1+e ^{-3.152 + 0.277(점) – 1.082(나눗셈)} )

예를 들어, 경기당 평균 20득점을 기록하고 Division 1에 출전하는 선수가 드래프트될 확률은 다음과 같이 계산할 수 있습니다.

확률 = e ^{-3.152 + 0.277(20) – 1.082(1)} / (1+e ^{-3.152 + 0.277(20) – 1.082(1)} ) = 0.787 .

이 확률은 0.5보다 크기 때문에 이 선수가 드래프트될 것이라고 예측할 수 있습니다.

4단계. 결과를 보고합니다.

마지막으로 로지스틱 회귀 분석 결과를 보고하고자 합니다. 이를 수행하는 방법의 예는 다음과 같습니다.

게임당 점수와 디비전 레벨이 농구 선수의 드래프트 확률에 어떤 영향을 미치는지 확인하기 위해 로지스틱 회귀 분석을 수행했습니다. 분석에는 총 14명의 플레이어가 사용되었습니다.

이 모델은 프로젝트 결과 변동의 72.5%를 설명하고 사례의 85.7%를 올바르게 분류했습니다.

Division 2 선수가 드래프트될 확률은 Division 1 선수가 드래프트될 확률의 0.339에 불과했습니다.

게임당 포인트가 추가로 한 단위 증가할 때마다 선수가 드래프트될 확률이 1,319씩 증가했습니다.