Z-점수가 음수가 될 수 있나요?

통계에서 z-점수는 값이 평균 에서 얼마나 많은 표준 편차를 가지고 있는지 알려줍니다. 다음 공식을 사용하여 z-점수를 계산합니다.

z = (X – μ) / σ

여기서 X는 분석 중인 값이고, μ는 평균, σ는 표준 편차입니다.

z 점수는 양수, 음수 또는 0일 수 있습니다.

양수 z 점수는 특정 값이 평균보다 높음을 나타내고 음수 z 점수는 특정 값이 평균보다 낮음을 나타내며 az 점수 0은 특정 값이 평균과 같음을 나타냅니다.

몇 가지 예를 통해 이를 명확하게 알 수 있습니다.

예: Z 점수 계산

특정 식물 그룹의 높이(인치)를 표시하는 다음 데이터세트가 있다고 가정해 보겠습니다.

5장, 7장, 7장, 8장, 9장, 10장, 13장, 17장, 17장, 18장, 19장, 19장, 20장

이 데이터 세트의 표본 평균은 13 이고 표본 표준 편차는 5.51 입니다.

1. 이 데이터세트에서 값 “8”에 대한 z-점수를 찾습니다.

Z-점수를 계산하는 방법은 다음과 같습니다.

z = (X – μ) / σ = (8 – 13) / 5.51 = -0.91

이는 값 “8”이 평균보다 0.91 표준편차 낮다 는 것을 의미합니다.

2. 이 데이터세트에서 값 “13”에 대한 z-점수를 찾습니다.

Z-점수를 계산하는 방법은 다음과 같습니다.

z = (X – μ) / σ = (13 – 13) / 5.46 = 0

이는 값 “13”이 평균과 정확히 동일하다는 것을 의미합니다.

3. 이 데이터세트에서 값 “20”에 대한 z-점수를 찾습니다.

Z-점수를 계산하는 방법은 다음과 같습니다.

z = (X – μ) / σ = (20 – 13) / 5.46 = 1.28

이는 값 “20”이 평균보다 1.28 표준편차 높다는 것을 의미합니다.

Z 점수를 해석하는 방법

AZ 차트는 특정 Z 점수 아래로 떨어지는 값의 비율을 알려줍니다. 몇 가지 예를 통해 이를 명확하게 알 수 있습니다.

예 1: 음수 Z 점수

앞서 우리는 데이터세트의 원시 값 “8”의 z 점수가 -0.91 이라는 것을 발견했습니다. Z 테이블에 따르면 이 값보다 낮은 값은 18.14%이다.

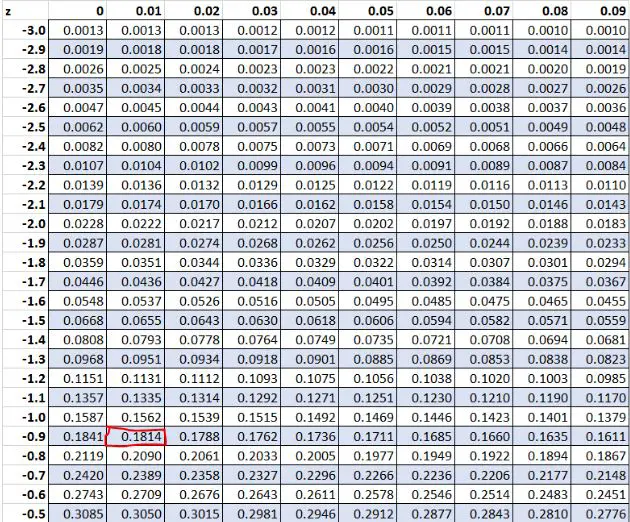
예 2: Z-점수는 0입니다.

앞서 우리는 데이터 세트의 원시 값 “13”의 z 점수가 0 이라는 것을 발견했습니다. Z 테이블에 따르면 값의 50.00%가 이 값보다 작습니다.

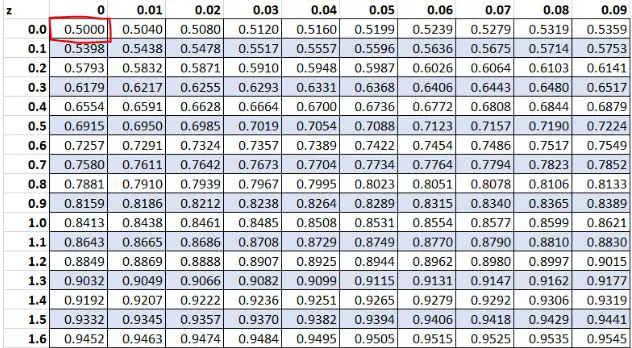
예 3: 양수 Z 점수

앞서 우리는 데이터 세트의 원시 값 “20”의 z 점수가 1.28 이라는 것을 발견했습니다. Z 테이블에 따르면 89.97%의 값이 이 값보다 낮습니다.

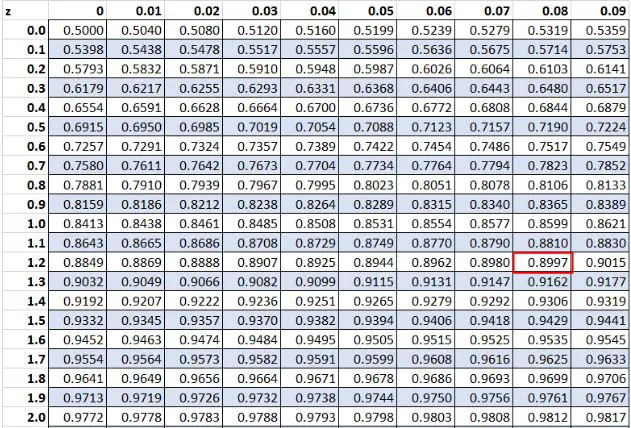
결론

Z 점수는 음의 무한대와 양의 무한대 사이의 값을 취할 수 있지만 대부분의 z 점수는 평균의 2 표준 편차 내에 있습니다. 실제로 통계에는 경험 법칙 이라는 규칙이 있는데, 이는 정규 분포를 갖는 주어진 데이터 세트에 대해 다음과 같이 명시합니다.

• 데이터 값의 68% 가 평균의 1표준편차 내에 있습니다.
• 데이터 값의 95% 가 평균의 2표준편차 내에 있습니다.
• 데이터 값의 99.7%가 평균의 3표준편차 내에 속합니다.

z-점수의 절대값이 높을수록 원시 값은 데이터 세트의 평균에서 더 멀어집니다. z-점수의 절대값이 낮을수록 원시 값은 데이터 세트의 평균에 더 가깝습니다.

관련 주제:

엄지손가락 계산기의 법칙
Excel에서 경험 법칙을 적용하는 방법