Sas에서 z 점수를 계산하는 방법

통계에서 z-점수는 값이 평균 에서 얼마나 많은 표준 편차를 가지고 있는지 알려줍니다.

다음 공식을 사용하여 z-점수를 계산합니다.

z = (X – μ) / σ

금:

• X는 단일 원시 데이터 값입니다.
• μ는 데이터 세트의 평균입니다.
• σ는 데이터 세트의 표준 편차입니다.

다음 예에서는 SAS에서 원시 데이터 값에 대한 z-점수를 계산하는 방법을 보여줍니다.

예: SAS에서 Z 점수 계산

SAS에서 다음 데이터 세트를 생성한다고 가정합니다.

 /*create dataset*/
data original_data;
    input values;
    datalines ;
7
12
14
12
16
18
6
7
14
17
19
22
24
13
17
12
;
run ;

/*view dataset*/
proc print data = original_data;

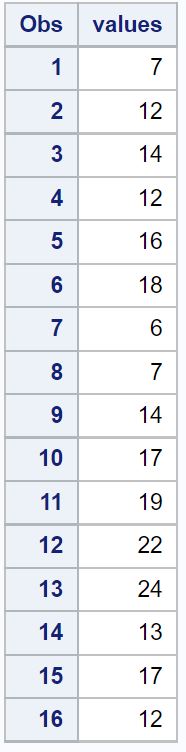
이제 데이터세트의 각 값에 대한 z-점수를 계산한다고 가정해 보겠습니다.

proc sql을 사용하여 이 작업을 수행할 수 있습니다.

 /*create new variable that shows z-scores for each raw data value*/
proc sql ;
    select values, (values - mean(values)) / std(values) as z_scores
    from original_data;
quit ; 

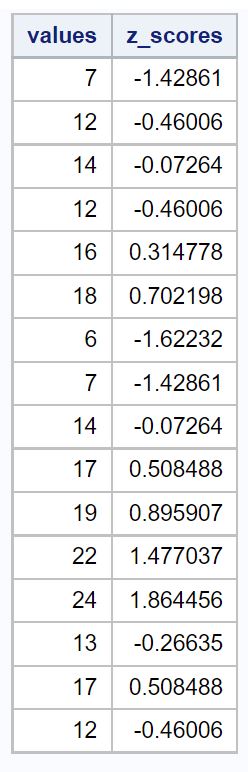
값 열에는 원본 데이터 값이 표시되고 z_scores 열에는 각 값에 대한 z 점수가 표시됩니다.

SAS에서 Z 점수를 해석하는 방법

z-점수는 값이 평균에서 얼마나 많은 표준 편차를 가지고 있는지 알려줍니다.

z 점수는 양수, 음수 또는 0일 수 있습니다.

양수 z 점수는 특정 값이 평균보다 높음을 나타내고 음수 z 점수는 특정 값이 평균보다 낮음을 나타내며 az 점수 0은 특정 값이 평균과 같음을 나타냅니다.

데이터 세트의 평균과 표준편차를 계산하면 평균은 14.375 이고 표준편차는 5.162 입니다.

따라서 데이터세트의 첫 번째 값은 7이었고 z 점수는 (7-14.375) / 5.162 = -1.428 이었습니다. 이는 값 “7”이 평균보다 1.428 표준편차 낮다 는 것을 의미합니다.

데이터의 다음 값인 12의 z-점수는 (12-14.375) / 5.162 = -0.46 입니다. 이는 값 “12”가 평균보다 0.46 표준편차 낮다 는 것을 의미합니다.

값이 평균에서 멀수록 해당 값에 대한 z-점수의 절대값이 더 높아집니다.

예를 들어, 값 7은 값 12보다 평균(14.375)에서 더 멀리 떨어져 있습니다. 이는 7의 절대값이 더 큰 z-점수를 갖는 이유를 설명합니다.

추가 리소스

다음 문서에서는 SAS에서 다른 일반적인 작업을 수행하는 방법을 설명합니다.

SAS에서 이상값을 식별하는 방법
SAS에서 백분위수를 계산하는 방법
SAS에서 평균, 중앙값 및 모드를 계산하는 방법