공분산

에 의해 벤자민 앤더슨 8월 5, 2023 통계 댓글 0개

이 문서에서는 공분산이 무엇인지, 그리고 계산 방법을 설명합니다. 공분산 공식과 데이터 세트의 공분산을 계산하는 예를 찾을 수 있습니다. 또한 마지막에 온라인 계산기를 사용하여 모든 데이터 계열의 공분산을 계산할 수 있습니다.

공분산이란 무엇입니까?

통계에서 공분산은 두 확률 변수의 결합 변동 정도를 나타내는 값입니다. 즉, 공분산은 두 변수 사이의 의존성을 분석하는 데 사용됩니다.

공분산은 두 변수의 데이터와 해당 평균 간의 차이를 곱한 값의 합을 총 데이터 수로 나눈 값과 같습니다.

👉 아래 계산기를 사용하여 모든 데이터 세트의 공분산을 계산할 수 있습니다.

공분산 값의 해석은 매우 간단합니다.

공분산이 양수 이면 두 변수 사이에 종속성이 있음을 의미합니다. 따라서 한 변수의 값이 증가하면 다른 변수의 값도 증가하며 그 반대의 경우도 마찬가지입니다.
공분산이 음수 이면 두 변수 간의 관계가 음수라는 의미입니다. 따라서 한 변수의 값이 증가하면 다른 변수의 값이 감소하고 그 반대의 경우도 마찬가지입니다.
공분산이 0 (또는 해당 값이 0에 가까움)인 경우 이는 두 변수 사이에 관계가 없음을 의미합니다. 즉, 두 확률변수는 서로 독립적입니다.

공분산을 계산하는 방법

데이터 계열의 공분산을 계산하려면 다음 단계를 수행해야 합니다.

각 변수의 평균을 개별적으로 계산합니다.
각 변수에 대해 각 값과 변수 평균 간의 차이를 찾습니다.
각 데이터 포인트에 대해 이전 단계에서 계산된 차이를 곱합니다.
이전 단계에서 얻은 모든 결과를 더합니다.
총 데이터 수로 나눕니다. 얻은 값은 데이터 계열의 공분산입니다.

요약하면 두 변수 간의 공분산을 계산하는 공식은 다음과 같습니다.

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

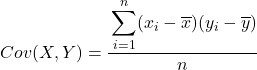
두 변수 간의 공분산을 추출하는 데 적극 권장되는 방법은 모든 데이터 쌍이 포함된 테이블을 만들고 위에 설명된 각 단계에 대한 열을 추가하는 것입니다. 이렇게 하면 계산이 훨씬 더 잘 구성되고 수행 중인 작업을 더 잘 이해할 수 있습니다.

공분산 계산의 예

공분산의 정의를 고려하면 다음은 이러한 유형의 통계 측정값을 계산하는 단계별 예입니다. 목표는 공분산의 개념과 두 변수 간의 상관 관계를 분석하는 방법을 더 잘 이해하는 것입니다.

다음 통계 데이터 세트의 공분산을 계산합니다.

먼저, 각 변수의 산술 평균을 계산해야 합니다. 이를 위해 각 변수의 값의 합을 전체 데이터 수로 나눕니다.

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ 참조: 산술 공식 평균

각 확률 변수의 평균을 결정한 후에는 데이터 테이블에 다음 열을 추가하여 공분산을 얻을 수 있습니다.

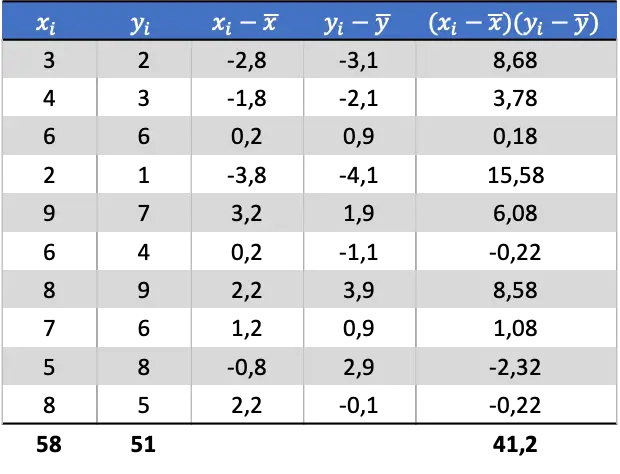
따라서 두 변수의 공분산을 결정하려면 마지막 열의 합계를 데이터 쌍의 수로 나누어야 합니다.

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

이 경우 공분산 값은 양수입니다. 이는 연구된 두 확률 변수 사이에 직접적인 의존성이 있음을 의미합니다. 그러나 공분산 값이 음수인 경우 이는 두 변수 간의 종속성이 반대임을 의미합니다. 그리고 마지막으로 공분산 값이 0이거나 0에 매우 가까우면 두 변수 사이에 선형 관계가 없다는 의미입니다.

이 예제를 풀어보면 알 수 있듯이 Excel과 같은 컴퓨터 프로그램을 사용하여 테이블에 열을 추가하고 빠르게 계산을 수행하는 것이 매우 유용합니다. 그렇지 않으면 작업을 수동으로 계산하여 공분산을 찾는 데 훨씬 더 오랜 시간이 걸립니다.