혼란스러운 변수는 무엇입니까? (정의 & #038; 예)

모든 실험에는 두 가지 주요 변수가 있습니다.

독립변수: 종속변수에 대한 효과를 관찰할 수 있도록 실험자가 수정하거나 제어하는 변수입니다.

종속 변수: 독립 변수에 “종속”되는 실험에서 측정된 변수입니다.

연구자들은 독립변수의 변화가 종속변수에 어떤 영향을 미치는지 이해하는 데 관심이 있는 경우가 많습니다.

그러나 때로는 세 번째 변수가 고려되지 않고 연구된 두 변수 간의 관계에 영향을 미칠 수 있는 경우가 있습니다.

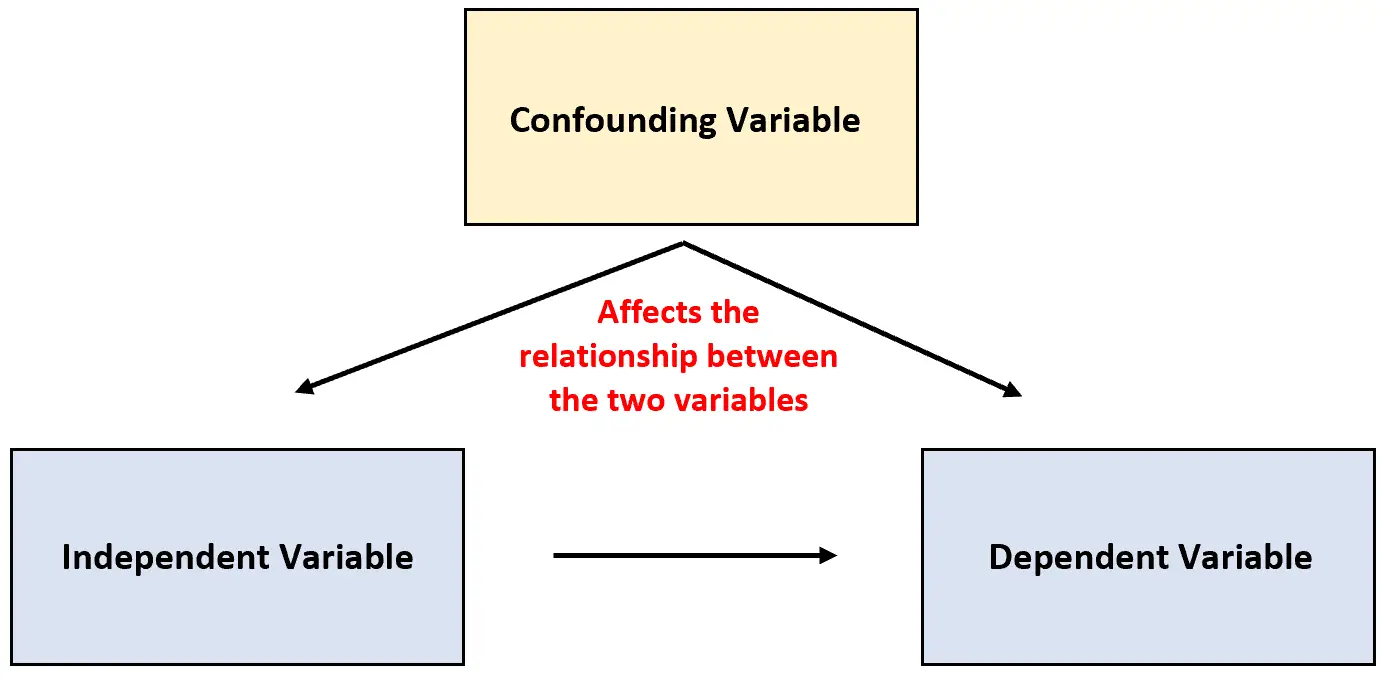
이러한 유형의 변수는 교란변수 로 알려져 있으며 연구 결과를 혼란스럽게 하고 두 변수 사이에 실제로 존재하지 않는 일종의 인과 관계가 있는 것처럼 보이게 할 수 있습니다.

교란변수(Confounding Variable): 실험에 포함되지는 않지만 실험에서 두 변수 사이의 관계에 영향을 미치는 변수.

이러한 유형의 변수는 실험 결과를 혼란스럽게 하고 신뢰할 수 없는 결과를 초래할 수 있습니다.

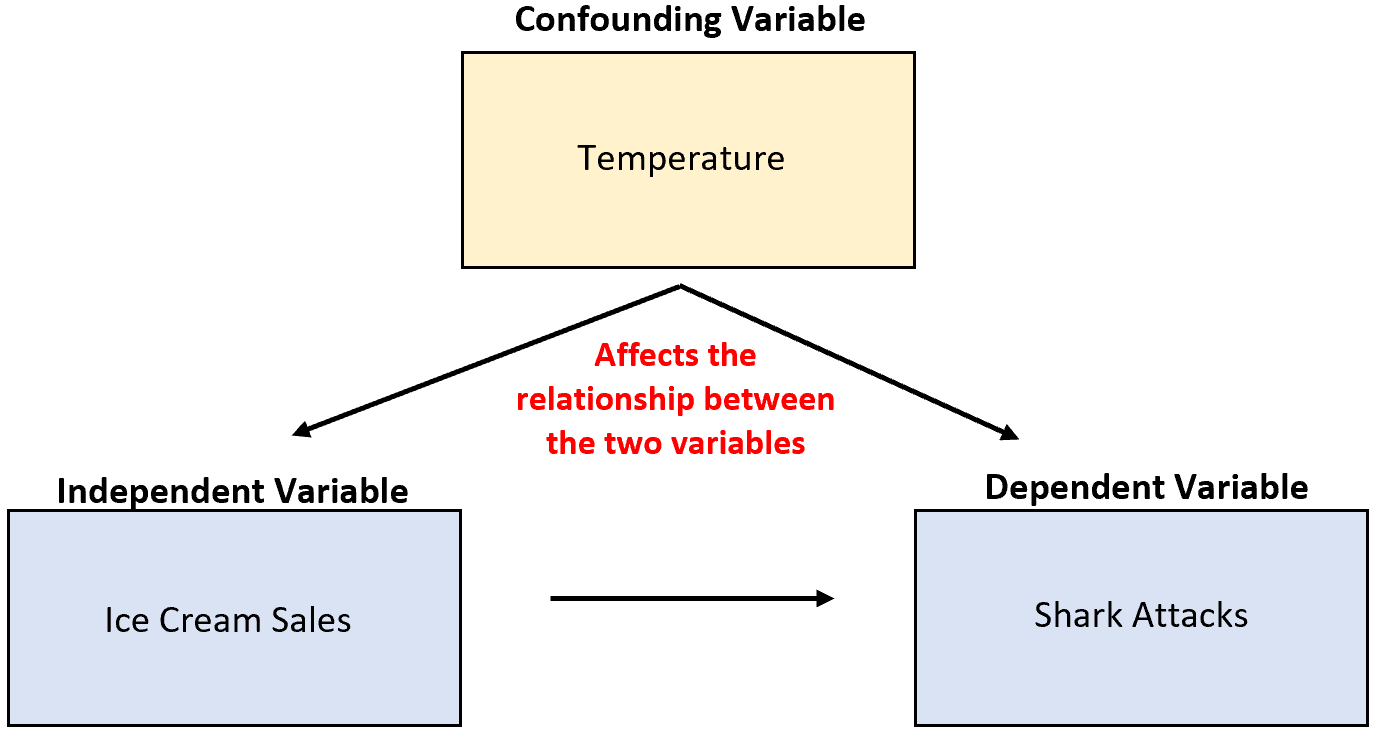
예를 들어, 연구자가 아이스크림 판매와 상어 공격에 대한 데이터를 수집하고 두 변수가 높은 상관 관계를 발견했다고 가정해 보겠습니다. 이것은 아이스크림 판매 증가로 인해 상어 공격이 더 많이 발생한다는 것을 의미합니까?

그럴 것 같지 않습니다. 가장 가능성이 높은 원인은 혼란스러운 가변 온도 입니다. 날씨가 따뜻해지면 아이스크림을 사먹는 사람이 늘어나고, 바다로 나가는 사람도 늘어납니다.

혼란스러운 변수에 대한 요구 사항

변수가 혼란스러운 변수가 되려면 다음 요구 사항을 충족해야 합니다.

1. 독립변수와 상관관계가 있어야 합니다.

이전 예에서 온도는 아이스크림 판매라는 독립변수와 상관관계가 있었습니다. 특히, 기온이 높을수록 아이스크림 판매량이 늘어나고, 기온이 낮아지면 판매량이 감소합니다.

2. 종속변수와 인과관계가 있어야 합니다.

이전 예에서 온도는 상어 공격 횟수에 직접적인 영향을 미쳤습니다. 특히 기온이 따뜻해지면 더 많은 사람이 바다로 몰려들게 되어 상어 공격 가능성이 직접적으로 높아집니다.

혼란스러운 변수가 왜 문제가 됩니까?

교란변수는 다음 두 가지 이유로 문제가 됩니다.

1. 교란변수는 원인과 결과 관계가 존재하지 않는데도 존재하는 것처럼 보이게 할 수 있습니다.

이전 예에서는 혼란스러운 온도 변수로 인해 아이스크림 판매와 상어 공격 사이에 인과 관계가 있는 것처럼 보였습니다.

그러나 우리는 아이스크림 판매가 상어 공격을 유발하지 않는다는 것을 알고 있습니다. 혼란스러운 온도 변수가 그렇게 보이게 만듭니다.

2. 교란 변수는 변수 간의 실제 원인과 결과 관계를 모호하게 만들 수 있습니다.

혈압을 낮추는 운동의 능력을 연구한다고 가정해 보겠습니다. 잠재적인 혼란 변수는 시작 체중인데, 이는 운동과 상관관계가 있고 혈압에 직접적인 인과 관계가 있습니다.

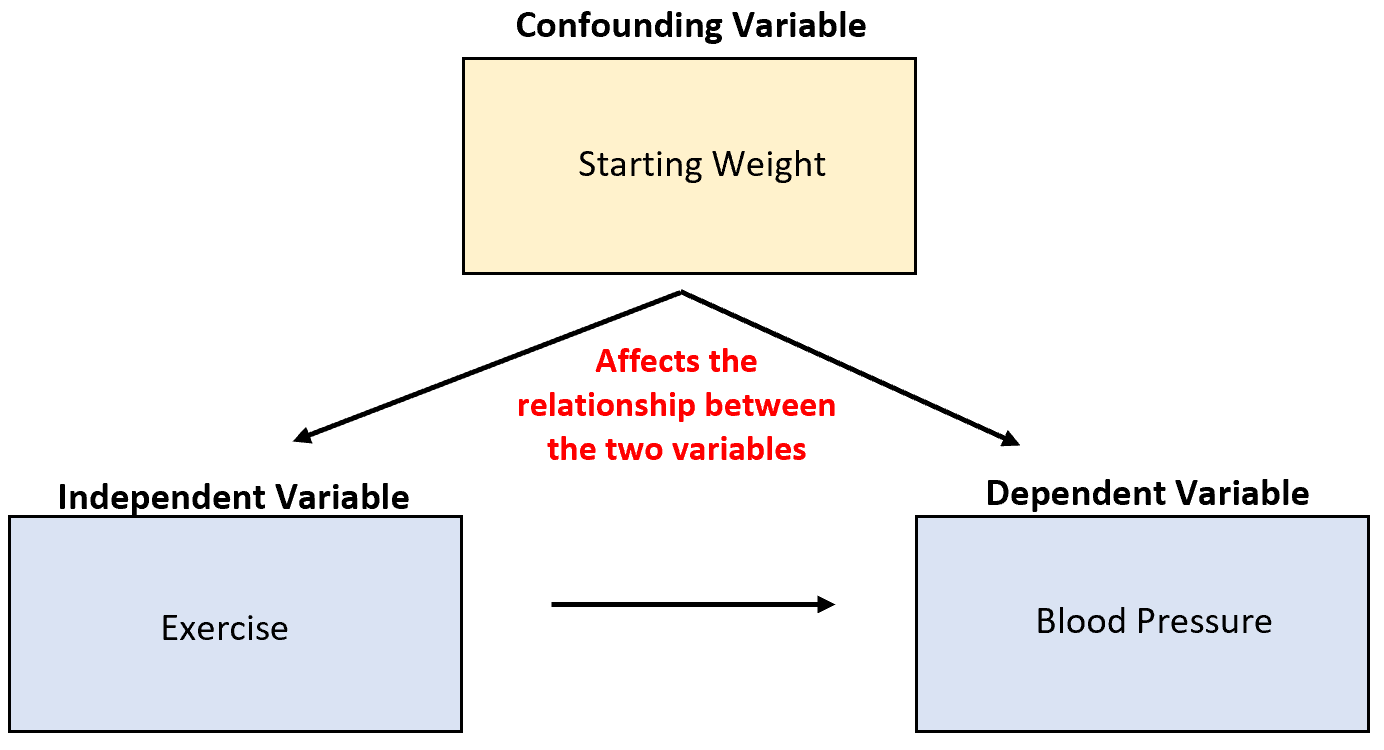
신체 활동이 증가하면 혈압이 감소할 수 있지만 개인의 시작 체중도 이 두 변수 사이의 관계에 큰 영향을 미칩니다.

혼란스러운 변수와 내부 타당성

기술적인 용어로 교란변수는 연구의 내부 타당성 에 영향을 미치며, 이는 종속 변수의 모든 변화를 독립 변수의 변화에 귀속시키는 타당성을 말합니다.

교란변수가 존재할 때 종속변수에서 관찰된 변화가 독립변수 변화의 직접적인 결과라고 항상 확실하게 말할 수는 없습니다.

혼란스러운 변수의 영향을 줄이는 방법

다음 방법을 포함하여 혼란스러운 변수의 영향을 줄이는 방법에는 여러 가지가 있습니다.

1. 무작위 배정

무작위 배정은 연구에 참여한 개인을 치료군 또는 대조군에 무작위로 배정하는 과정을 의미합니다.

예를 들어, 새로운 약이 혈압에 미치는 영향을 연구한다고 가정해 보겠습니다. 연구에 참여할 100명을 모집하는 경우 난수 생성기를 사용하여 50명을 대조군(약 없음)에 무작위로 할당하고 50명을 치료 그룹(새 약)에 할당할 수 있습니다.

무작위 할당을 사용하면 두 그룹이 대략 유사한 특성을 가질 가능성이 높아집니다. 즉, 두 그룹 간에 관찰되는 모든 차이는 처리에 따른 것일 수 있습니다.

이는 연구가 내부 타당성을 가져야 함을 의미합니다. 즉, 그룹 내 개인 간의 차이가 아니라 그룹 간의 혈압 차이를 알약 자체에 귀속시키는 것이 타당합니다.

2. 차단

차단이란 교란 변수의 영향을 제거하기 위해 교란 변수의 특정 값을 기준으로 연구에서 개인을 “블록”으로 나누는 관행을 의미합니다.

예를 들어, 연구자들이 체중 감량에 대한 새로운 식단의 효과를 이해하고 싶어한다고 가정해 보겠습니다. 독립변수는 새로운 식단이고 종속변수는 체중 감소량이다.

그러나 체중 감량의 변화를 일으킬 수 있는 혼란스러운 변수 중 하나는 성별 입니다. 새로운 다이어트의 효과 여부에 관계없이 개인의 성별이 체중 감량에 영향을 미칠 가능성이 높습니다.

이 문제를 해결하는 한 가지 방법은 개인을 다음 두 블록 중 하나에 배치하는 것입니다.

• 남성
• 여성

그런 다음 각 블록 내에서 개인을 두 가지 치료법 중 하나에 무작위로 할당합니다.

• 새로운 다이어트
• 표준 다이어트

이렇게 하면 각 블록 내 변동이 모든 개인 간의 변동보다 훨씬 낮아질 것이며, 성별을 조절하면서 새로운 식단이 체중 감량에 어떤 영향을 미치는지 더 잘 이해할 수 있을 것입니다.

3. 대응

일치 쌍 설계는 잠재적 교란 변수의 값을 기반으로 개인을 “일치”하는 실험 설계의 한 유형입니다.

예를 들어, 연구자들이 표준 식단과 비교하여 새로운 식단이 체중 감량에 어떤 영향을 미치는지 알고 싶어한다고 가정해 보겠습니다. 이 상황에서 혼동될 수 있는 두 가지 변수는 연령 과 성별 입니다.

이를 설명하기 위해 연구원 100명의 피험자를 모집한 다음 연령과 성별을 기준으로 50쌍으로 그룹화합니다. 예를 들어:

• 25세 남성은 연령과 성별 측면에서 ‘일치’하므로 다른 25세 남성과 매칭됩니다.
• 30세 여성은 나이, 성별 등이 일치하므로 다른 30세 여성과 매칭됩니다.

그런 다음, 각 쌍 내에서 한 피험자는 무작위로 30일 동안 새로운 식단을 따르도록 배정되고 다른 피험자는 30일 동안 표준 식단을 따르도록 배정됩니다.

30일이 지나면 연구자들은 각 피험자의 총 체중 감소를 측정합니다.

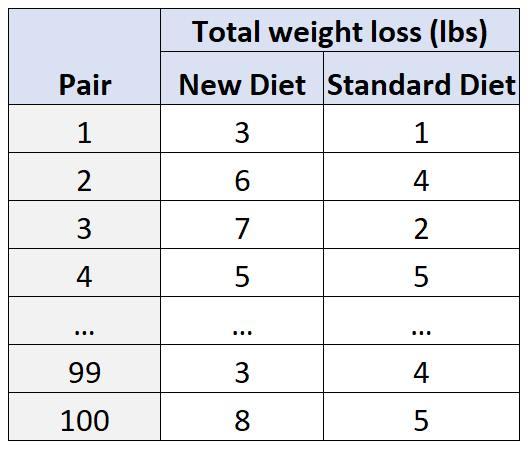
이러한 유형의 설계를 사용함으로써 연구자들은 체중 감량의 차이가 나이 와 성별 이라는 교란 변수보다는 사용된 다이어트 유형에 기인할 수 있음을 확신할 수 있습니다.

이러한 유형의 디자인에는 다음과 같은 몇 가지 단점이 있습니다.

1. 한 과목이라도 탈락하면 두 과목을 잃습니다. 피험자가 연구를 중단하기로 결정하면 더 이상 완전한 쌍이 없기 때문에 실제로 두 피험자를 잃게 됩니다.

2. 일치하는 항목을 찾는 데 시간이 걸립니다 . 성별, 연령 등 특정 변수와 일치하는 주제를 찾는 데는 시간이 많이 걸릴 수 있습니다.

3. 주제를 완벽하게 일치시킬 수 없습니다 . 아무리 노력해도 각 쌍의 주제에는 항상 변화가 있을 것입니다.

그러나 연구에 이 설계를 구현하는 데 사용할 수 있는 리소스가 있는 경우 교란 변수의 영향을 제거하는 데 매우 효과적일 수 있습니다.