균일 분포 소개

균일분포(uniform distribution) 는 a 에서 b까지 의 구간 사이의 각 값이 동일한 확률로 나타나는 확률분포이다.

확률 변수 X가 균일 분포를 따르는 경우 X가 x ₁ 과 x ₂ 사이의 값을 가질 확률은 다음 공식으로 찾을 수 있습니다.

P(x ₁ < X < x ₂ ) = (x ₂ – x ₁ ) / (b – a)

금:

• x ₁ : 낮은 이자값
• x ₂ : 관심 상한값
• a: 가능한 최소값
• b: 가능한 최대값

예를 들어, 돌고래의 체중이 100파운드에서 150파운드 사이에 균등하게 분포되어 있다고 가정해 보겠습니다.

돌고래를 무작위로 선택하면 위 공식을 사용하여 선택한 돌고래의 무게가 120~130파운드 사이일 확률을 결정할 수 있습니다.

• P(120 < X < 130) = (130 – 120) / (150 – 100)
• P(120 < X < 130) = 10/50
• P(120 < X < 130) = 0.2

선택한 돌고래의 몸무게가 120~130파운드일 확률은 0.2 입니다.

균등분포 시각화

균일 분포를 시각화하기 위해 밀도 플롯을 생성하면 다음 플롯과 같습니다.

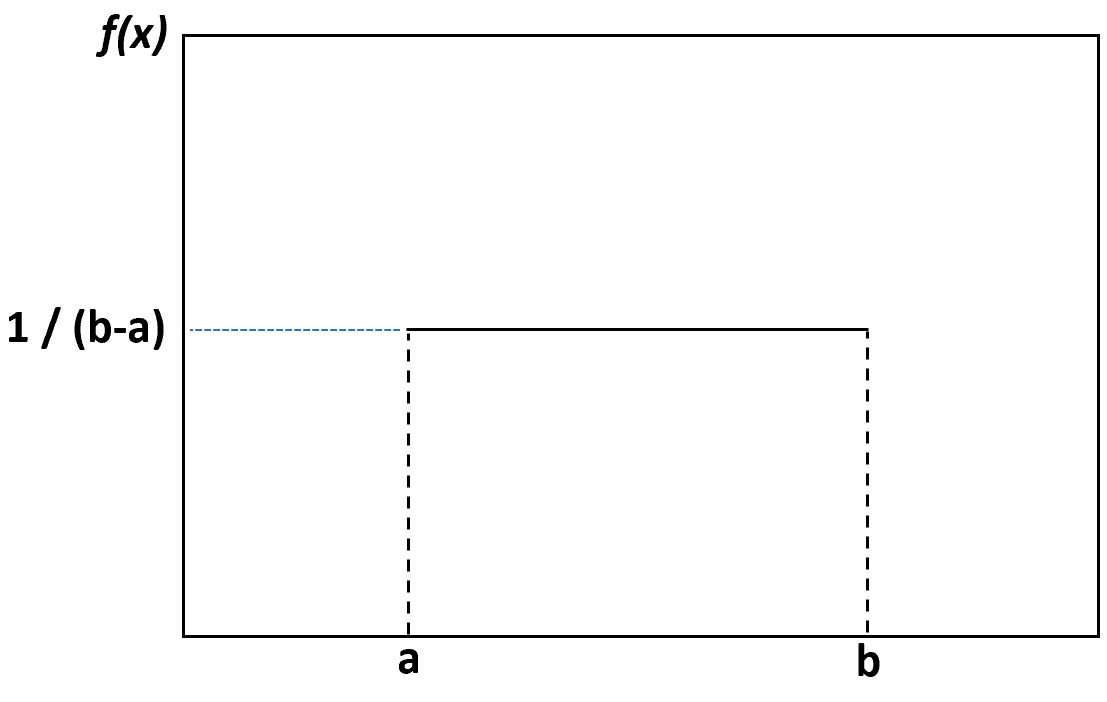
하한 a 와 상한 b 사이의 모든 값은 동일한 발생 확률을 가지며 이 한계를 벗어나는 값은 확률이 0입니다.

예를 들어, 이전 예에서는 돌고래의 무게가 100파운드에서 150파운드 사이에 균등하게 분포되어 있다고 말했습니다. 이 분포를 시각화하는 방법은 다음과 같습니다.

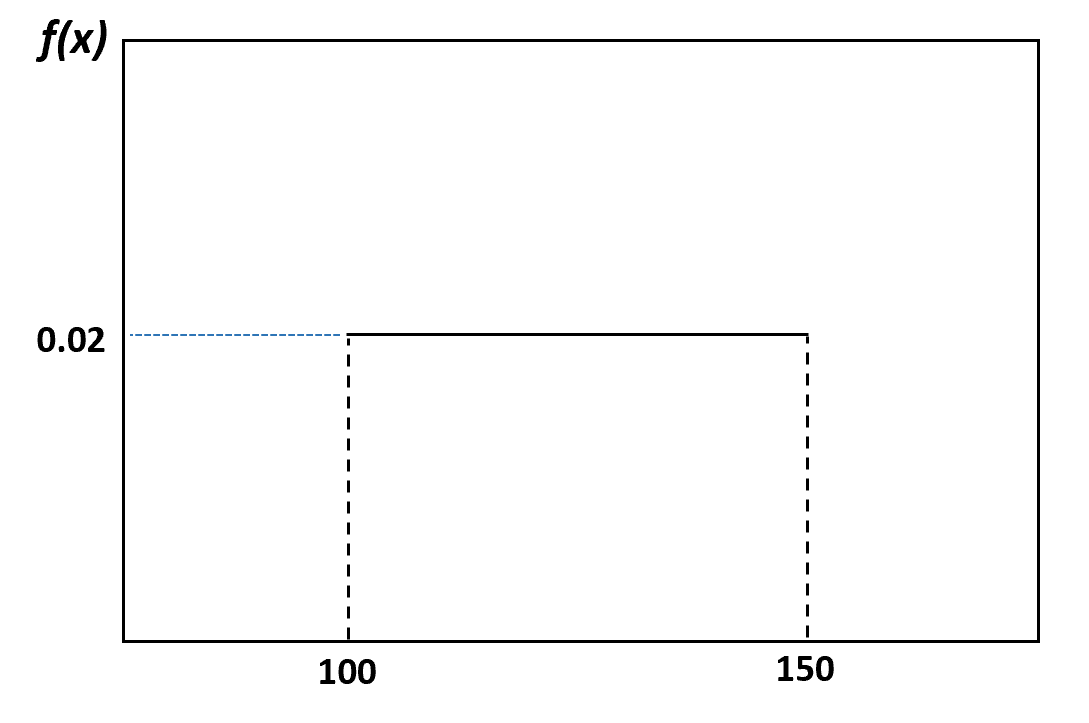
무작위로 선택한 돌고래의 무게가 120~130파운드일 확률은 다음과 같이 시각화할 수 있습니다.

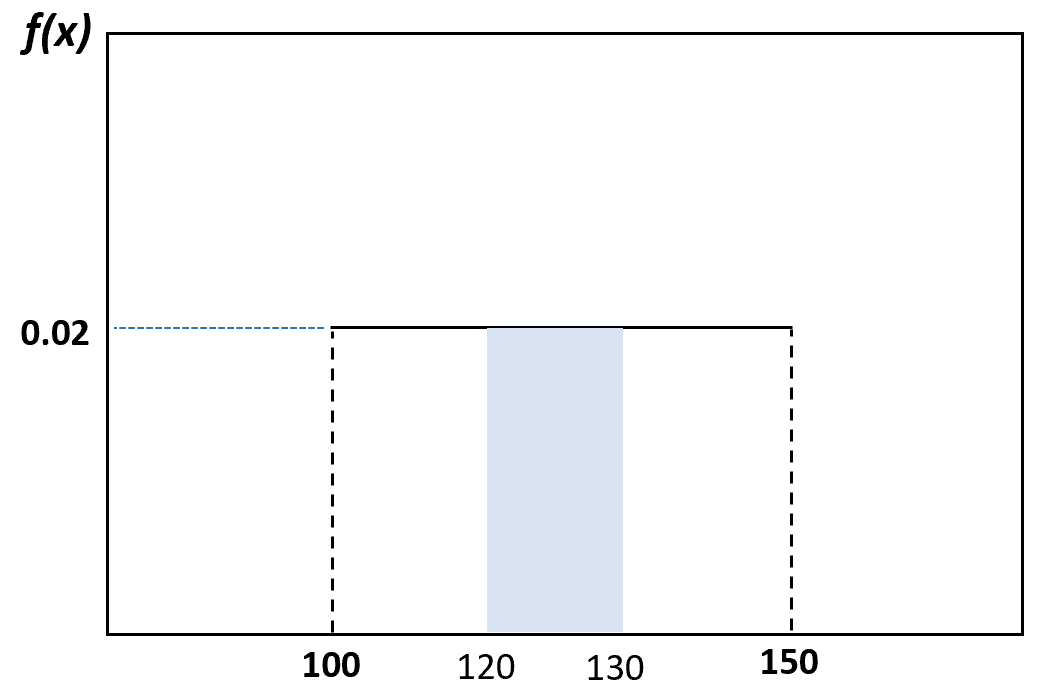
균등분포의 성질

균일 분포에는 다음과 같은 속성이 있습니다.

• 평균: (a + b) / 2
• 중앙값: (a + b) / 2
• 표준편차: √ (b – a) ² / 12
• 차이: (b – a) ² / 12

예를 들어, 돌고래의 체중이 100파운드에서 150파운드 사이에 균등하게 분포되어 있다고 가정해 보겠습니다.

이 분포에 대해 다음 속성을 계산할 수 있습니다.

• 평균 가중치: (a + b) / 2 = (150 + 100) / 2 = 125
• 중앙값 가중치: (a + b) / 2 = (150 + 100) / 2 = 125
• 무게의 표준편차: √ (150 – 100) ² / 12 = 14.43
• 무게 변화: (150 – 100) ² / 12 = 208.33

균일한 배포 관행 관련 문제

균일 분포에 대한 지식을 테스트하려면 다음 연습 문제를 사용하세요.

질문 1: 버스는 20분마다 버스 정류장에 옵니다. 버스 정류장에 도착했다면 버스가 8분 이내에 도착할 확률은 얼마입니까?

해결 방법 1: 최소 대기 시간은 0분이고 최대 대기 시간은 20분입니다. 하한 이자값은 0분, 상한 이자값은 8분입니다.

따라서 우리는 다음과 같이 확률을 계산합니다.

P(0 < X < 8) = (8-0) / (20-0) = 8/20 = 0.4 .

질문 2: NBA 경기 시간은 120분에서 170분 사이에 균등하게 분배됩니다. 무작위로 선택한 NBA 게임이 155분 이상 지속될 확률은 얼마입니까?

해결 방법 2: 최소 지속 시간은 120분이고 최대 지속 시간은 170분입니다. 하한 이자 값은 155분이고 상한 이자 값은 170분입니다.

따라서 우리는 다음과 같이 확률을 계산합니다.

P(155 < X < 170) = (170-155) / (170-120) = 15/50 = 0.3 .

질문 3: 특정 개구리 종의 무게는 15~25g으로 고르게 분포되어 있습니다. 개구리를 무작위로 선택하면 무게가 17~19g일 확률은 얼마입니까?

해결 방법 3: 최소 무게는 15g이고 최대 무게는 25g입니다. 하한 이자 값은 17g이고 상한 이자 값은 19g입니다.

따라서 우리는 다음과 같이 확률을 계산합니다.

P(17 < X < 19) = (19-17) / (25-15) = 2/10 = 0.2 .

참고: 균일 분포 계산기를 사용하여 이러한 각 문제에 대한 답을 확인할 수 있습니다.