그룹화된 데이터의 범위를 찾는 방법: 예 포함

우리는 종종 어떤 방식으로든 함께 그룹화된 데이터의 범위를 계산하려고 합니다.

범위 는 데이터 세트에서 가장 큰 값과 가장 작은 값의 차이를 나타냅니다.

예를 들어 다음과 같이 그룹화된 데이터가 있다고 가정합니다.

원시 데이터 값을 모르기 때문에 정확한 범위를 계산할 수는 없지만 다음 공식 중 하나를 사용하여 범위를 추정하는 것은 가능합니다.

공식 1: 상한 및 하한 사용

그룹화된 데이터 범위 = U _max – L _min

금:

• U : 최대 간격의 상한
• L : 최소 간격의 하한

공식 2: 중간점 사용

그룹화된 데이터 범위 = _최대 중간점 – _최소 중간점

금:

• _Max Mid : 최대 간격의 중간점
• Middle _min : 최소 간격의 중간점

다음 예에서는 실제로 각 수식을 사용하는 방법을 보여줍니다.

예시 1: 그룹화된 데이터 범위 계산

특정 수업에서 40명의 학생이 채점한 시험을 보여주는 다음과 같은 빈도 분포가 있다고 가정합니다.

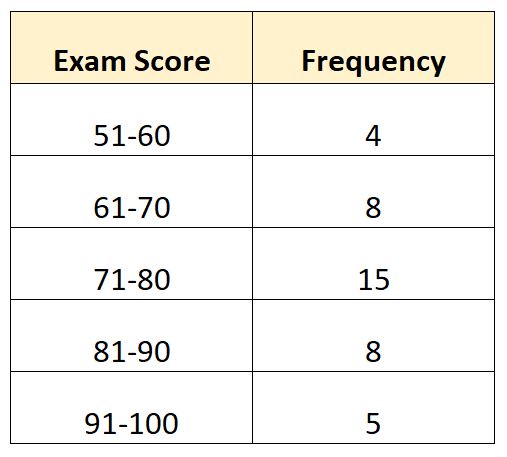
각 수식을 사용하여 그룹화된 데이터의 범위를 계산하는 방법은 다음과 같습니다.

공식 1: 상한 및 하한 사용

• 그룹화된 데이터 범위 = U _max – L _min
• 그룹화된 데이터 범위 = 100 – 51
• 그룹화된 데이터 범위 = 49

이 공식을 사용하여 범위는 49 로 추정됩니다.

공식 2: 중간점 사용

• 그룹화된 데이터 범위 = _최대 중간점 – _최소 중간점
• 그룹화된 데이터 범위 = (100+91)/2 – (60+51)/2
• 그룹화된 데이터 범위 = 95.5 – 55.5
• 그룹화된 데이터 범위 = 40

이 공식을 사용하여 범위를 40 으로 추정합니다.

예시 2: 그룹화된 데이터 범위 계산

60명의 농구 선수가 경기당 득점한 점수를 보여주는 다음과 같은 빈도 분포가 있다고 가정합니다.

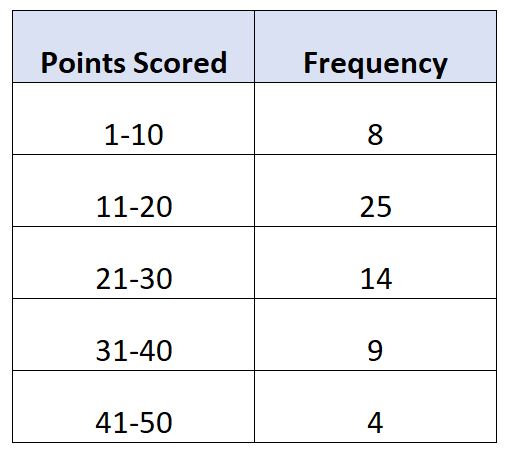
각 수식을 사용하여 그룹화된 데이터의 범위를 계산하는 방법은 다음과 같습니다.

공식 1: 상한 및 하한 사용

• 그룹화된 데이터 범위 = U _max – L _min
• 그룹화된 데이터 범위 = 50 – 1
• 그룹화된 데이터 범위 = 49

이 공식을 사용하여 범위는 49 로 추정됩니다.

공식 2: 중간점 사용

• 그룹화된 데이터 범위 = _최대 중간점 – _최소 중간점
• 그룹화된 데이터 범위 = (50+41)/2 – (1+10)/2
• 그룹화된 데이터 범위 = 45.5 – 5.5
• 그룹화된 데이터 범위 = 40

이 공식을 사용하여 범위를 40 으로 추정합니다.

추가 리소스

다음 튜토리얼에서는 그룹화된 데이터를 사용하여 다른 일반적인 작업을 수행하는 방법을 설명합니다.

그룹화된 데이터의 평균과 표준편차를 찾는 방법
그룹화된 데이터의 중앙값을 찾는 방법
그룹화된 데이터의 분산을 찾는 방법
그룹화된 데이터의 백분위수 순위를 계산하는 방법