Excel에서 다중 선형 회귀를 수행하는 방법
다중 선형 회귀는 둘 이상의 설명 변수와 응답 변수 간의 관계를 이해하는 데 사용할 수 있는 방법입니다.
이 튜토리얼에서는 Excel에서 다중 선형 회귀를 수행하는 방법을 설명합니다.
참고: 설명 변수가 하나만 있는 경우 대신 단순 선형 회귀를 수행해야 합니다.
예: Excel의 다중 선형 회귀
공부한 시간과 준비 시험의 횟수가 학생이 특정 대학 입학 시험에서 받는 성적에 영향을 미치는지 알고 싶다고 가정해 보겠습니다.
이 관계를 탐색하기 위해 학습 시간 과 준비 시험을 설명 변수로, 시험 결과를 반응 변수로 사용하여 다중 선형 회귀를 수행할 수 있습니다.
다중 선형 회귀를 수행하려면 Excel에서 다음 단계를 완료하세요.
1단계: 데이터를 입력합니다.
20명의 학생에 대해 공부한 시간, 치른 준비 시험, 받은 시험 결과에 대해 다음 데이터를 입력합니다.
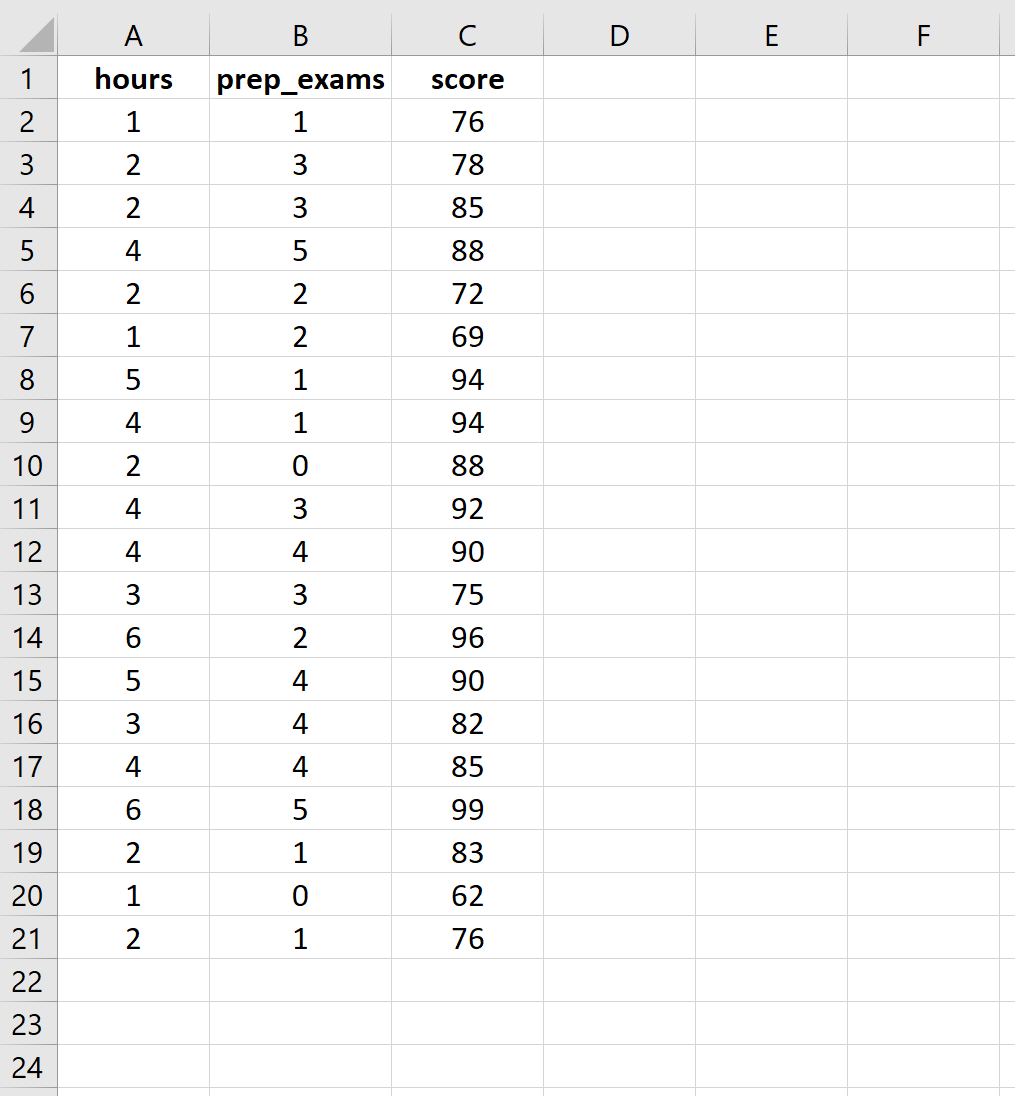
2단계: 다중 선형 회귀를 수행합니다.
Excel 상단 리본에서 데이터 탭으로 이동하여 데이터 분석을 클릭합니다. 이 옵션이 표시되지 않으면 먼저 무료 Analysis ToolPak 소프트웨어를 설치 해야 합니다.

데이터 분석을 클릭하면 새 창이 나타납니다. 회귀를 선택하고 확인을 클릭합니다.
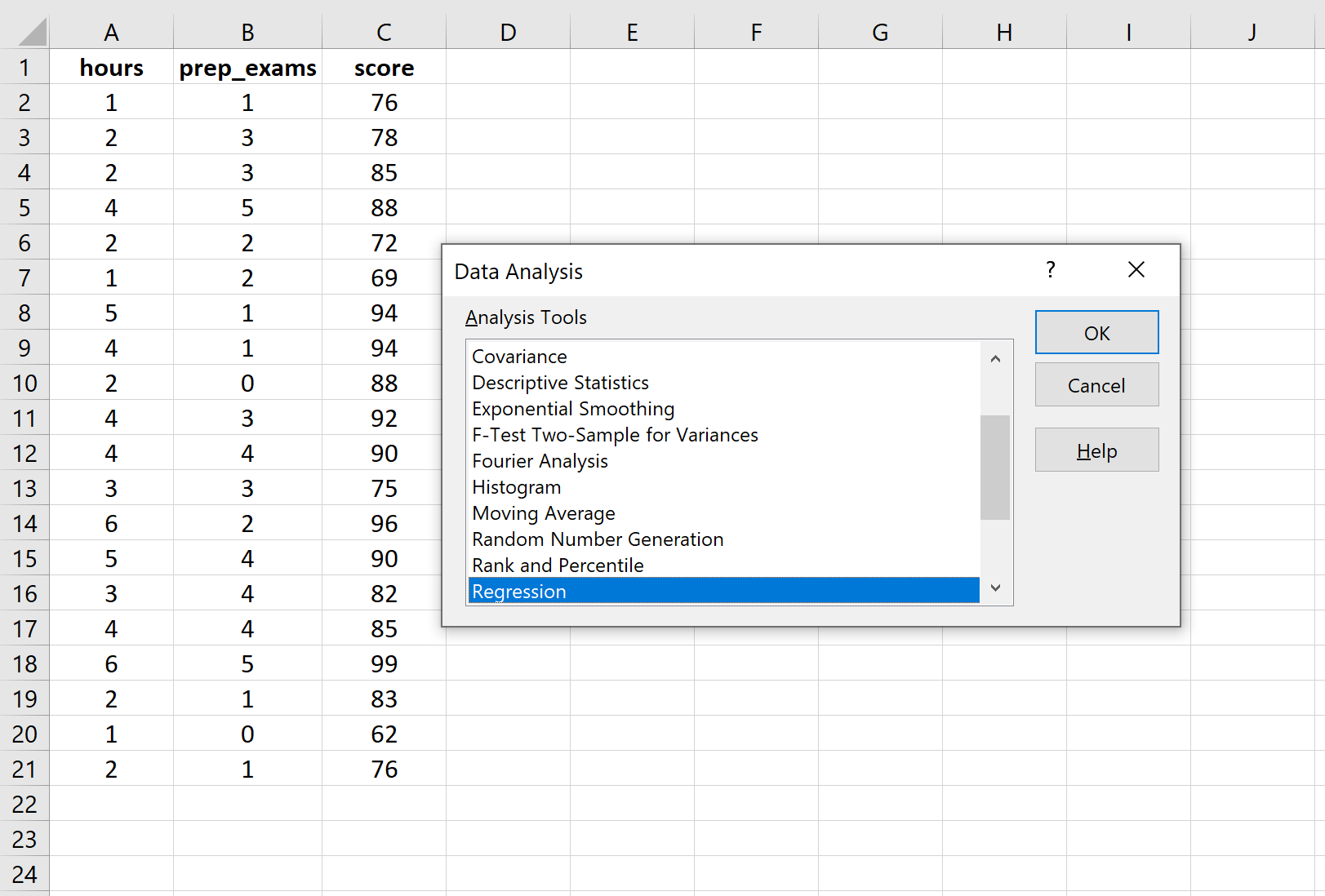
입력 Y 범위 의 경우 응답 변수에 대한 값 배열을 채웁니다. 입력 X 범위(Input X Range) 에 두 설명 변수에 대한 값 배열을 채웁니다. 입력 범위에 변수 이름이 포함되었음을 Excel에 알리려면 레이블 옆의 확인란을 선택합니다. 출력 범위 에서 회귀 결과를 표시할 셀을 선택합니다. 그런 다음 확인을 클릭합니다.
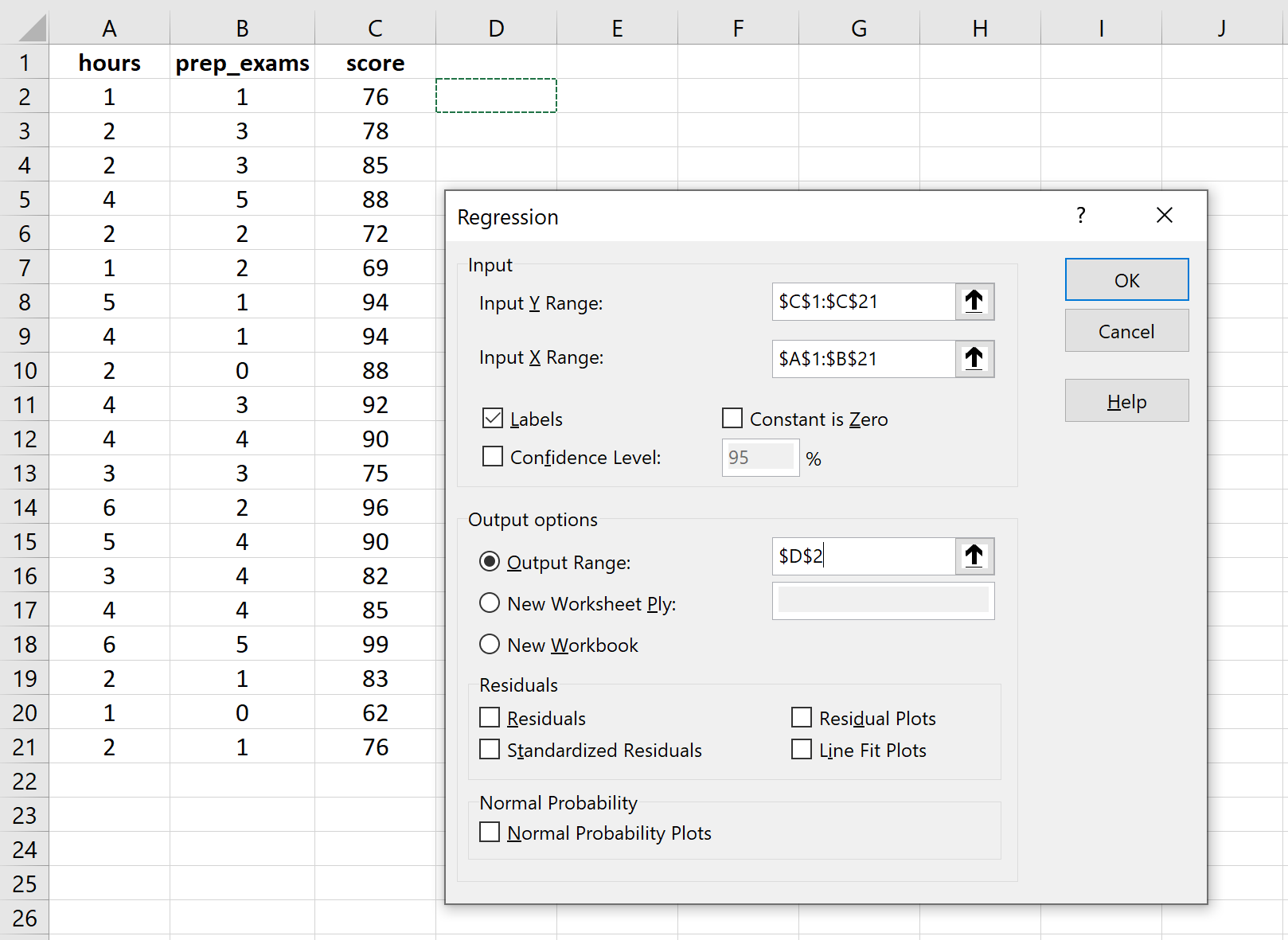
다음 출력이 자동으로 나타납니다.

3단계: 결과를 해석합니다.
결과에서 가장 관련성이 높은 숫자를 해석하는 방법은 다음과 같습니다.
R 제곱: 0.734 . 이것을 결정계수라고 합니다. 설명변수로 설명할 수 있는 반응변수의 분산의 비율입니다. 이 예에서 시험 점수 변동의 73.4%는 공부한 시간과 응시한 준비 시험 횟수로 설명됩니다.
표준 오류: 5.366 . 이는 관찰된 값과 회귀선 사이의 평균 거리입니다. 이 예에서 관측값은 회귀선에서 평균 5,366단위만큼 벗어납니다.
F: 오후 11시 46분 이는 회귀 모델에 대한 전체 F 통계이며 회귀 MS/잔차 MS로 계산됩니다.
F: 0.0000을 의미합니다 . 이는 전체 F 통계량과 관련된 p-값입니다. 이는 회귀 모델 전체가 통계적으로 유의미한지 여부를 알려줍니다. 즉, 결합된 두 설명변수가 반응변수와 통계적으로 유의미한 연관성을 갖는지 여부를 알려줍니다. 이 경우 p-값은 0.05 미만으로 설명 변수 , 공부 시간 , 준비 시험을 합친 것이 시험 결과 와 통계적으로 유의미한 연관성이 있음을 나타냅니다.
P-값. 개별 p-값은 각 설명 변수가 통계적으로 유의한지 여부를 알려줍니다. 공부한 시간은 통계적으로 유의미한 반면(p = 0.00), 응시한 준비 시험 (p = 0.52)은 α = 0.05에서 통계적으로 유의하지 않음을 알 수 있습니다. 과거의 준비 시험은 통계적으로 유의미하지 않기 때문에 결국 모델에서 이를 제거하기로 결정할 수도 있습니다.
계수: 각 설명 변수의 계수는 다른 설명 변수가 일정하다고 가정할 때 응답 변수의 예상 평균 변화를 알려줍니다. 예를 들어, 연습 시험이 일정하게 유지된다는 가정 하에 공부하는 데 추가 시간을 소비할 때마다 평균 시험 점수는 5.56 씩 증가할 것으로 예상됩니다.
이를 다르게 보는 방법은 다음과 같습니다. 학생 A와 학생 B가 모두 같은 수의 준비 시험을 치르지만 학생 A가 한 시간 더 공부한다면 학생 A는 학생 B보다 5.56 점 더 높은 점수를 받아야 합니다.
우리는 인터셉트 계수를 해석하여 시간도 공부하지 않고 준비 시험도 치르지 않은 학생의 예상 시험 점수가 67.67 임을 의미합니다.
추정 회귀 방정식: 모델 출력의 계수를 사용하여 다음과 같은 추정 회귀 방정식을 만들 수 있습니다.
시험 점수 = 67.67 + 5.56*(시간) – 0.60*(준비 시험)
이 추정 회귀 방정식을 사용하여 학습 시간과 응시하는 연습 시험 횟수를 기반으로 학생의 예상 시험 점수를 계산할 수 있습니다. 예를 들어, 3시간 동안 공부하고 시험을 치르는 학생은 83.75 점을 받아야 합니다.
시험 점수 = 67.67 + 5.56*(3) – 0.60*(1) = 83.75
과거 준비 시험은 통계적으로 유의미하지 않았기 때문에(p=0.52) 전체 모델에 어떠한 개선도 제공하지 않으므로 제거하기로 결정할 수도 있습니다. 이 경우 연구된 시간 만을 설명 변수로 사용하여 간단한 선형 회귀를 수행할 수 있습니다.
이 단순 선형 회귀 분석의 결과는 여기에서 확인할 수 있습니다.
추가 리소스
다중 선형 회귀를 수행한 후에는 다음을 포함한 여러 가정을 확인할 수 있습니다.
1. VIF를 사용한 다중공선성 테스트 .