다항 분포
이 기사에서는 통계에서 다항 분포가 무엇인지 설명합니다. 따라서 다항 분포의 정의, 공식, 해결된 연습 및 이러한 유형의 확률 분포의 속성을 찾을 수 있습니다. 또한 온라인 계산기를 사용하여 다항 분포의 확률을 계산할 수 있습니다.
다항 분포란 무엇입니까?
다항 분포 (또는 다항 분포 )는 여러 번의 시행 후에 주어진 횟수만큼 상호 배타적인 여러 사건이 발생할 확률을 설명하는 확률 분포입니다.
즉, 무작위 실험을 통해 3개 이상의 배타적 사건이 발생할 수 있고 각 사건이 개별적으로 발생할 확률을 알고 있는 경우, 여러 실험을 수행했을 때 특정 수의 사건이 발생할 확률을 계산하기 위해 다항 분포를 사용합니다. 매번 시간.
따라서 다항 분포는 이항 분포를 일반화한 것입니다.
다항 분포 공식
다항 분포 확률을 계산하려면 먼저 전체 데이터 수의 계승과 각 사건의 발생 횟수의 계승 사이의 몫을 구하고 그 결과에 각 사건의 확률을 곱해야 합니다. 해당 이벤트의 발생 횟수를 가져옵니다.
즉, 다항 분포의 공식은 다음과 같습니다.

금:
-
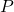
계산된 다항 분포의 확률입니다.
-

수행된 총 테스트 수입니다.
-

이벤트가 발생한 횟수입니다.

.
-

사건이 일어날 확률이다

.
👉 아래 계산기를 사용하여 다항 분포를 따르는 변수의 확률을 계산할 수 있습니다.
다항 분포 예
다항 분포의 개념 이해를 마치기 위해 아래에서 다항 분포의 확률을 계산하는 예를 해결했습니다.
- 한 상점에서는 세 가지 다른 제품을 판매합니다. 고객이 구매할 때 제품 A, 제품 B, 제품 C가 될 확률은 각각 30%, 15%, 55%입니다. 매장에서 8개 제품을 판매했을 때 2개는 A 제품, 1개는 제품 B, 5개는 제품 C일 확률을 구합니다.
정의된 문제는 다항 분포에 의해 관리되므로 이러한 유형의 확률 분포에 대한 공식을 적용해야 합니다.
![]()
따라서 문제의 데이터를 공식에 대체하고 확률 계산을 수행합니다.
![]()
따라서 문제 설명에서 말하는 내용이 발생할 확률은 11.4%입니다.
다항 분포 계산기
첫 번째 상자에는 각 사건의 발생 횟수를 적고, 두 번째 상자에는 각 사건의 발생 확률을 같은 순서로 적습니다. 그런 다음 마지막 공백에 시도한 총 횟수를 입력합니다.
데이터는 공백으로 구분해야 하며 소수점 구분 기호로 마침표를 사용하여 입력해야 합니다.
다항 분포의 속성
다항 분포에는 다음과 같은 특징이 있습니다.
- 다항 분포에서 n번의 시행을 실행할 때 사건 i 가 발생하는 횟수의 기대값은 수행된 총 시행 횟수에 사건이 발생할 확률을 곱한 값과 같습니다.
![]()
- 다항 분포에서 사건 i 에 대한 분산은 다음 식을 사용하여 계산됩니다.
![]()
- 마찬가지로, 두 사건 간의 공분산은 총 시행 횟수에 각 사건의 확률을 곱하고 -1을 곱한 것과 같습니다.
![]()
- 다항 분포의 적률 생성 함수는 다음과 같습니다.