Google 스프레드시트의 다항식 회귀(단계별)

회귀 분석은 하나 이상의 예측 변수와 반응 변수 간의 관계를 수량화하는 데 사용됩니다.

가장 일반적인 유형의 회귀 분석은 단순 선형 회귀 로, 예측 변수와 반응 변수가 선형 관계를 가질 때 사용됩니다.

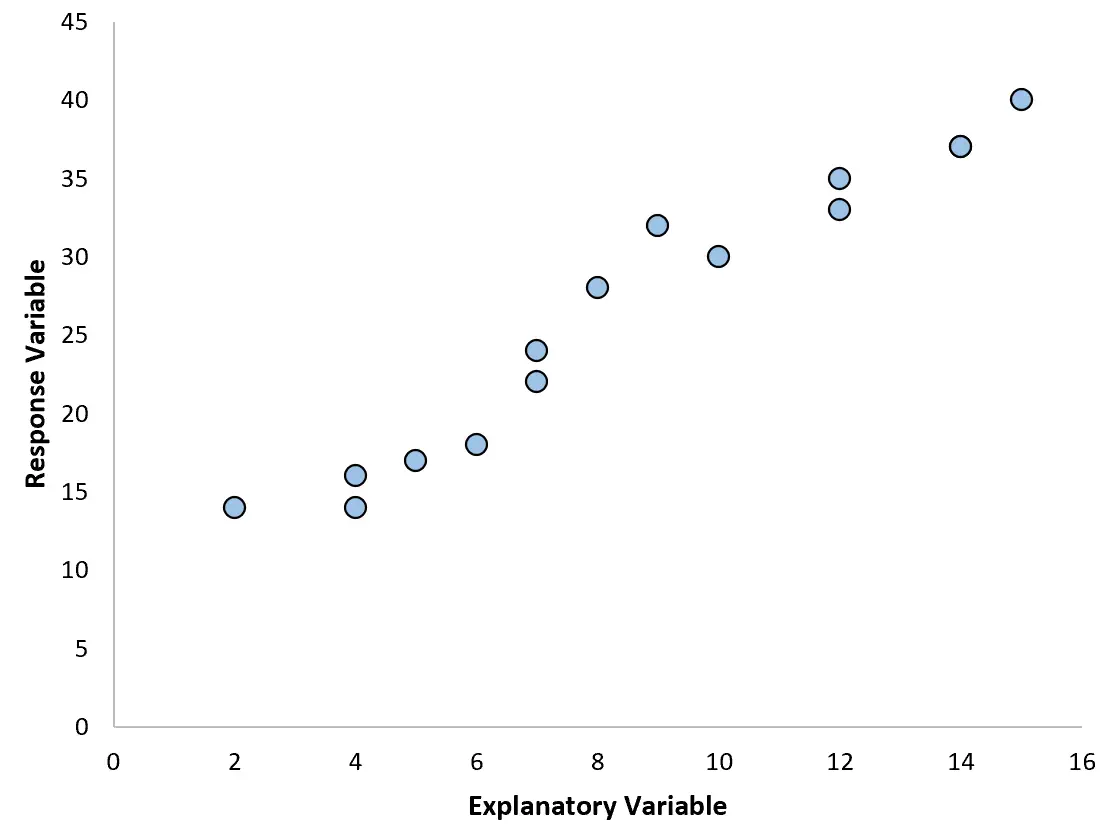
그러나 예측 변수와 반응 변수 간의 관계가 비선형인 경우도 있습니다.

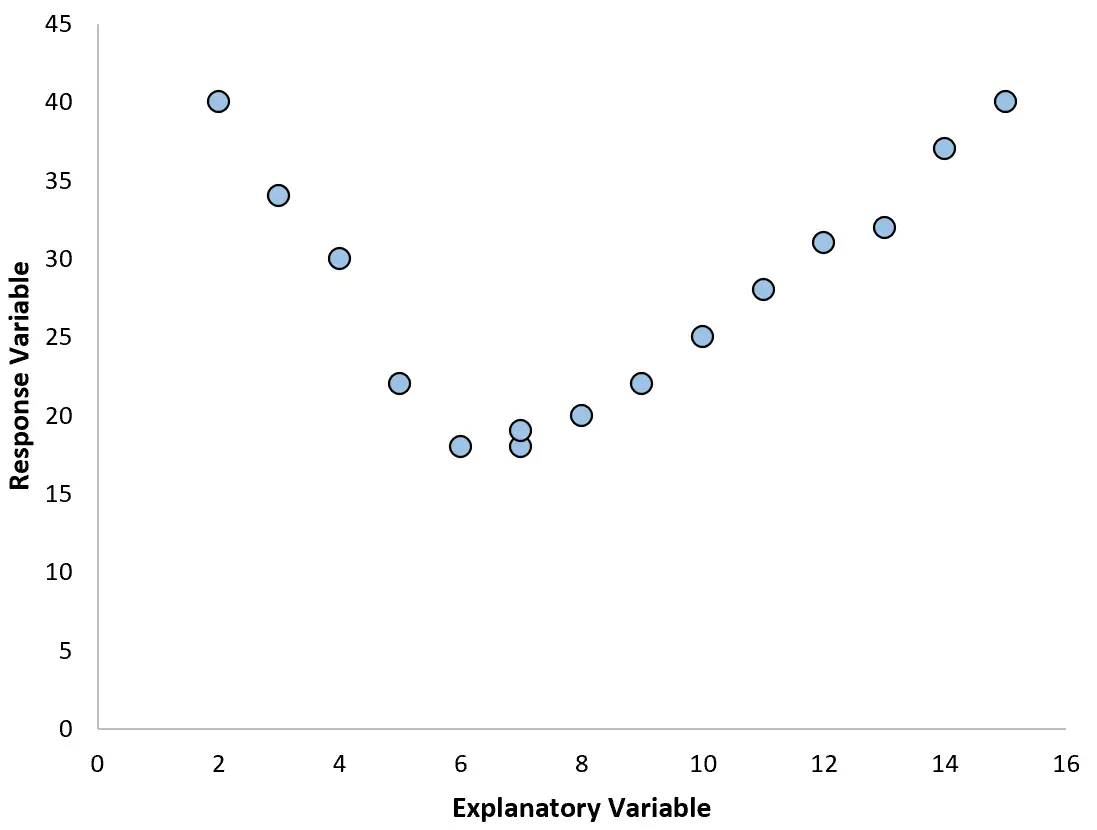
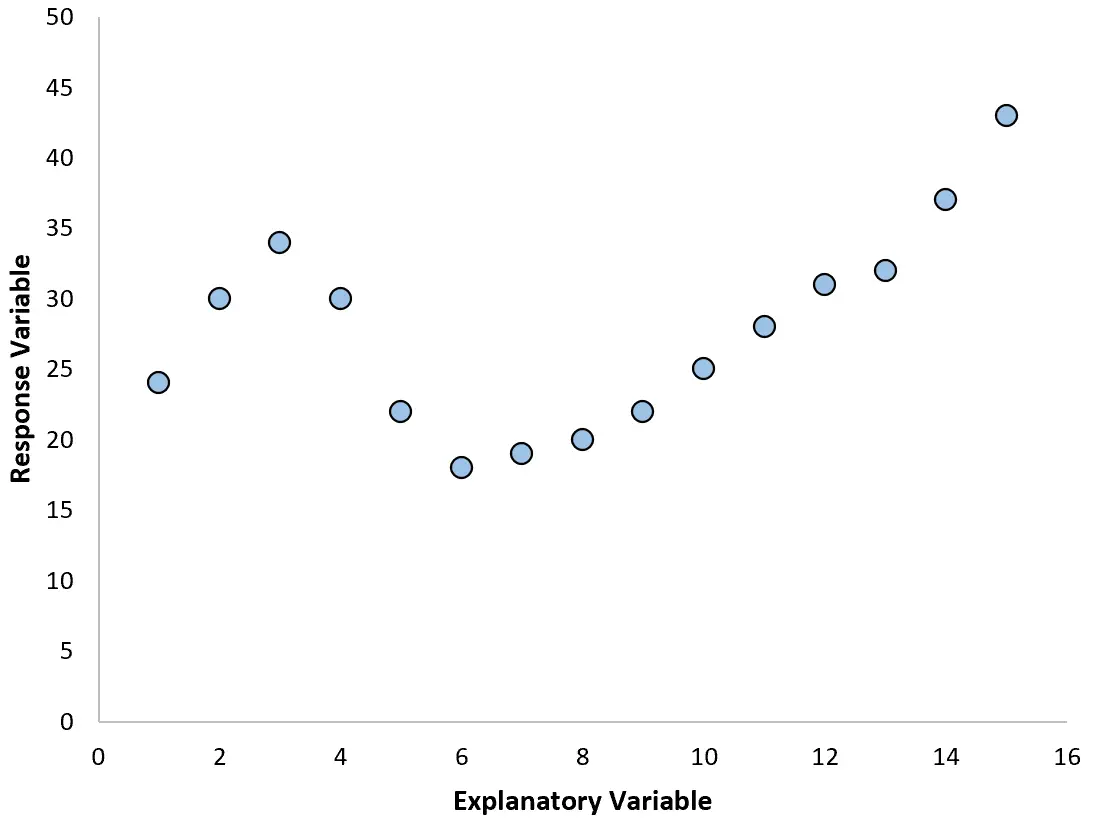
이러한 경우 변수 간의 비선형 관계를 설명할 수 있는 다항식 회귀를 사용하는 것이 좋습니다.

이 튜토리얼에서는 Google Sheets에서 다항식 회귀를 수행하는 방법에 대한 단계별 예를 제공합니다.

1단계: 데이터 생성

먼저 다음 값을 사용하여 가짜 데이터세트를 만들어 보겠습니다.

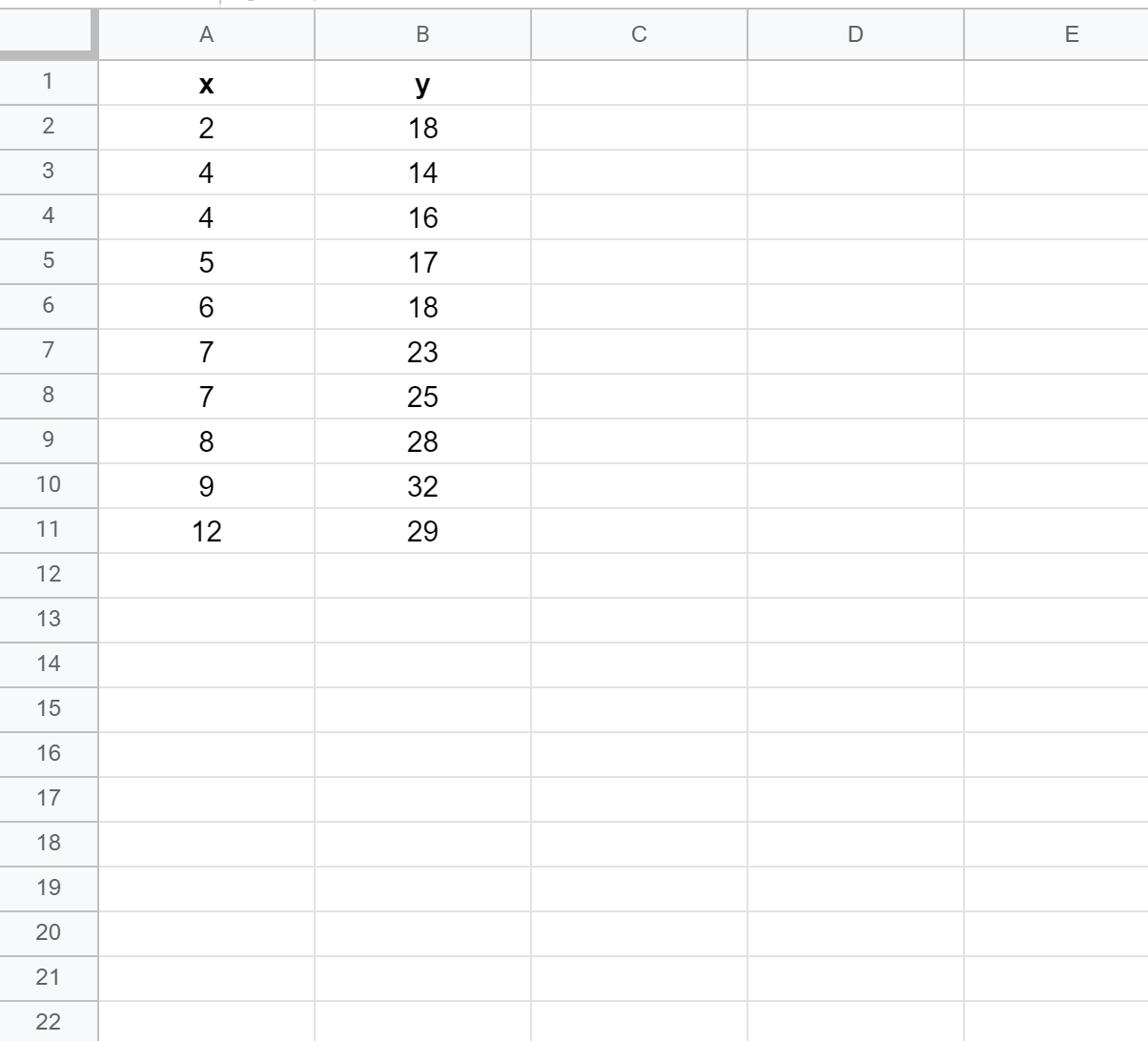
2단계: 산점도 만들기

다음으로, 데이터를 시각화하기 위해 산점도를 생성하겠습니다.

먼저 다음과 같이 A2:B11 셀을 강조 표시합니다.

그런 다음 삽입 탭을 클릭하고 드롭다운 메뉴에서 차트를 클릭합니다.

기본적으로 Google 스프레드시트는 산점도를 삽입합니다.

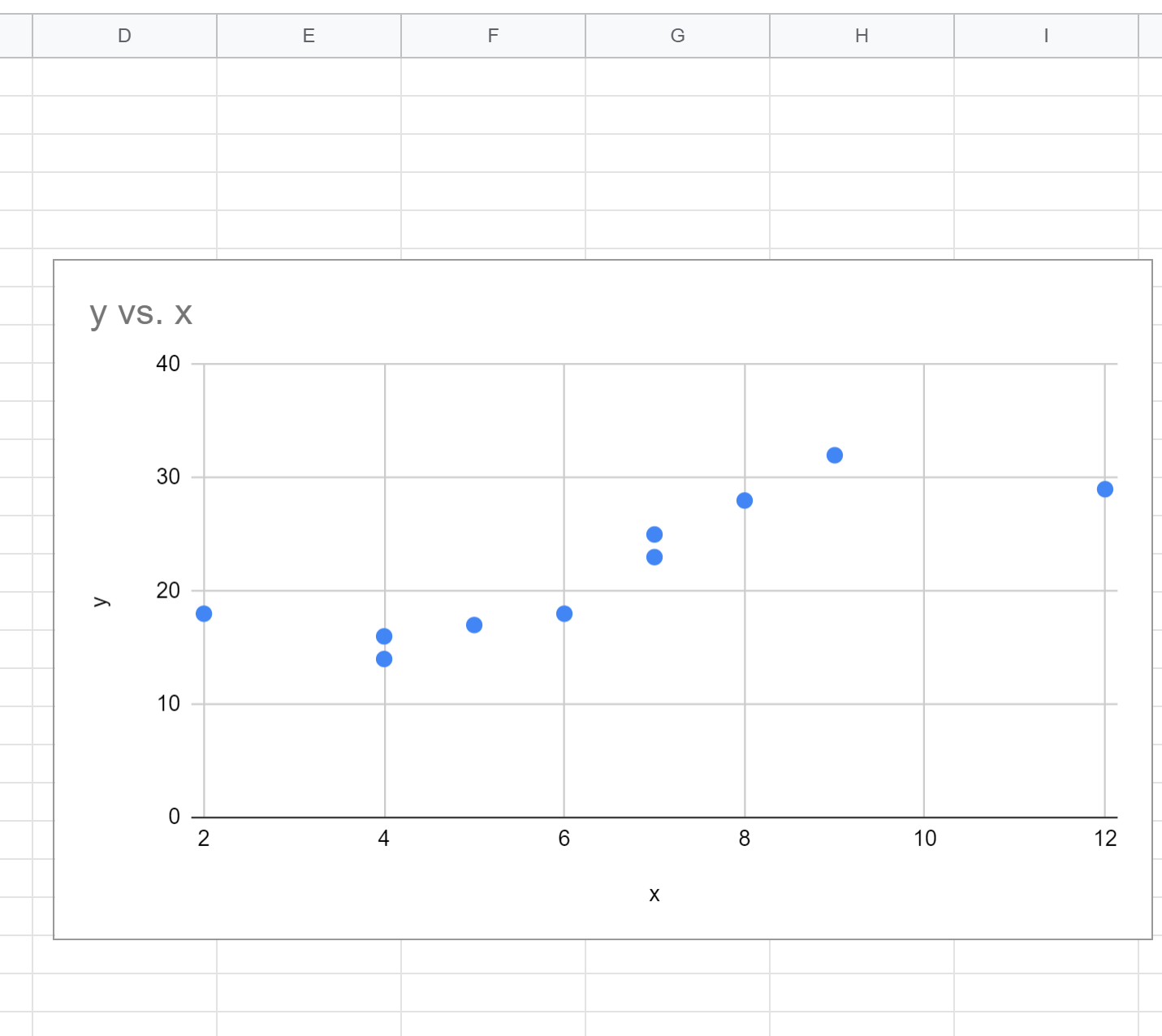
3단계: 다항식 회귀 방정식 찾기

그런 다음 산점도의 아무 곳이나 두 번 클릭하면 오른쪽에 그래프 편집기 창이 표시됩니다.

다음으로 시리즈 를 클릭하세요 . 그런 다음 아래로 스크롤하여 추세선 옆의 확인란을 선택하고 유형을 다항식 으로 변경합니다. 레이블에서 방정식 사용 을 선택한 다음 ^R2 표시 옆의 확인란을 선택합니다.

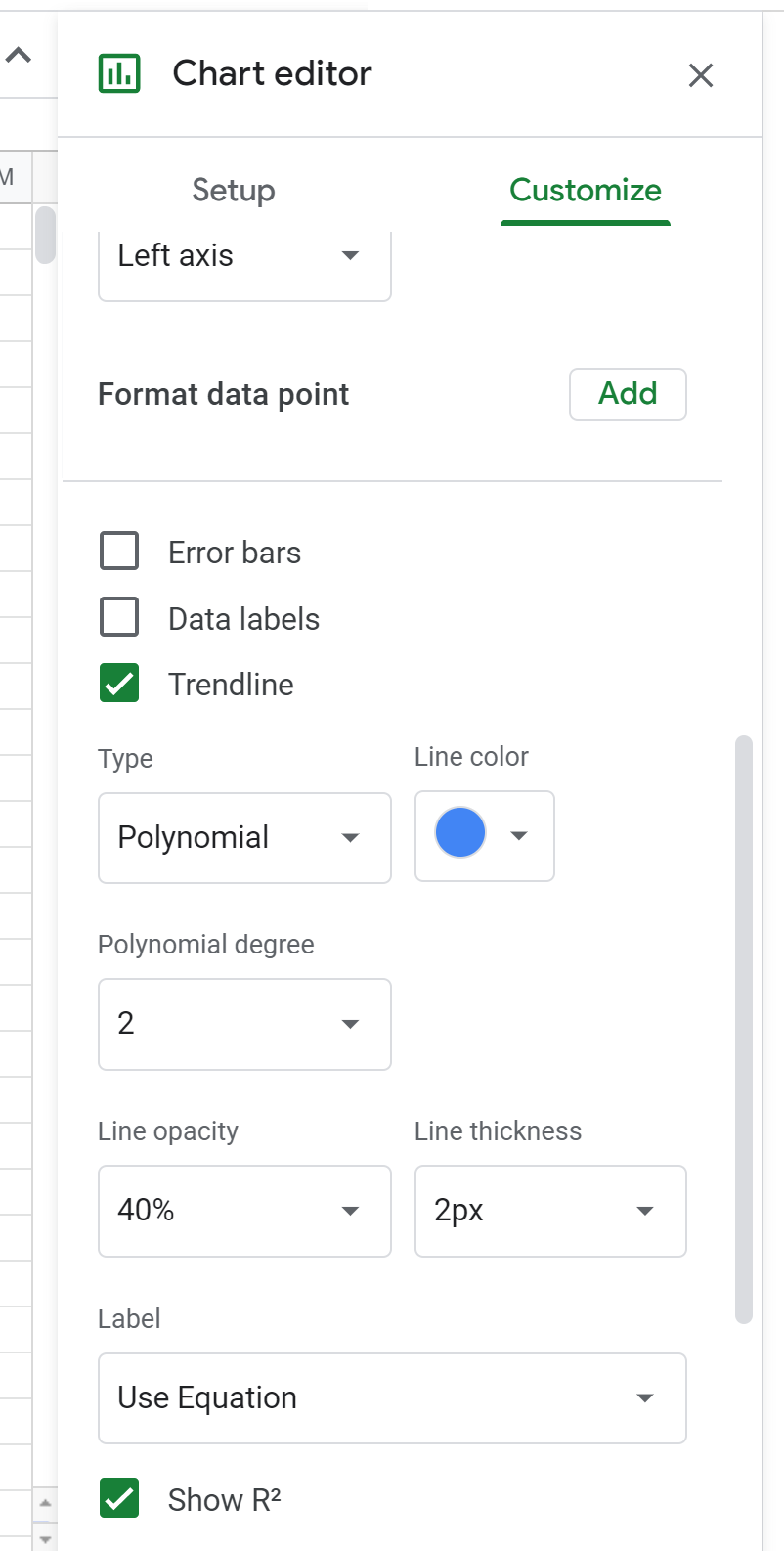
그러면 산점도 위에 다음 공식이 표시됩니다.

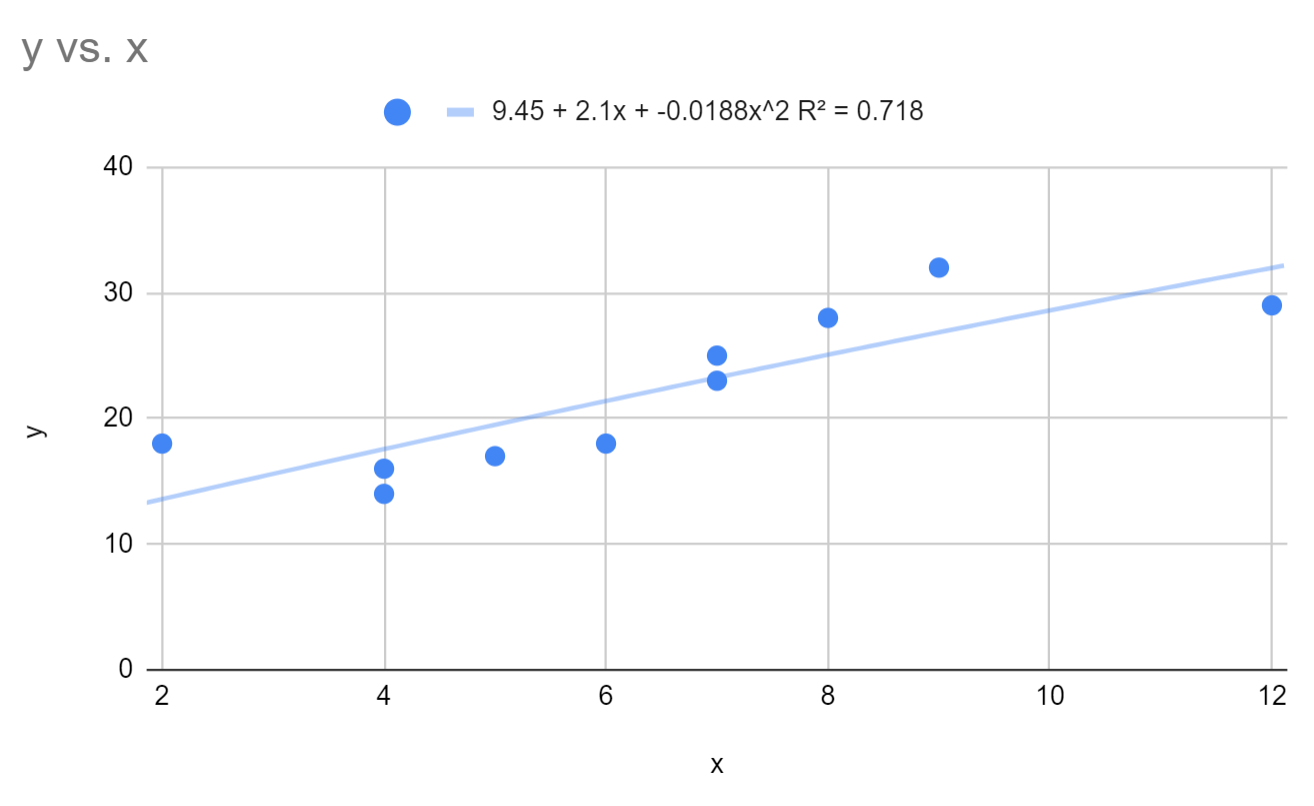
적합 다항식 회귀 방정식은 다음과 같습니다.

y = 9.45 + 2.1x – 0.0188x ²

이 모델의 R-제곱은 0.718 입니다.

R 제곱은 예측 변수로 설명할 수 있는 반응 변수의 변동 비율을 알려준다는 점을 기억하세요. 값이 높을수록 모델이 더 좋아집니다.

다음으로 그래프 편집기에서 다항식의 차수를 3으로 변경합니다.

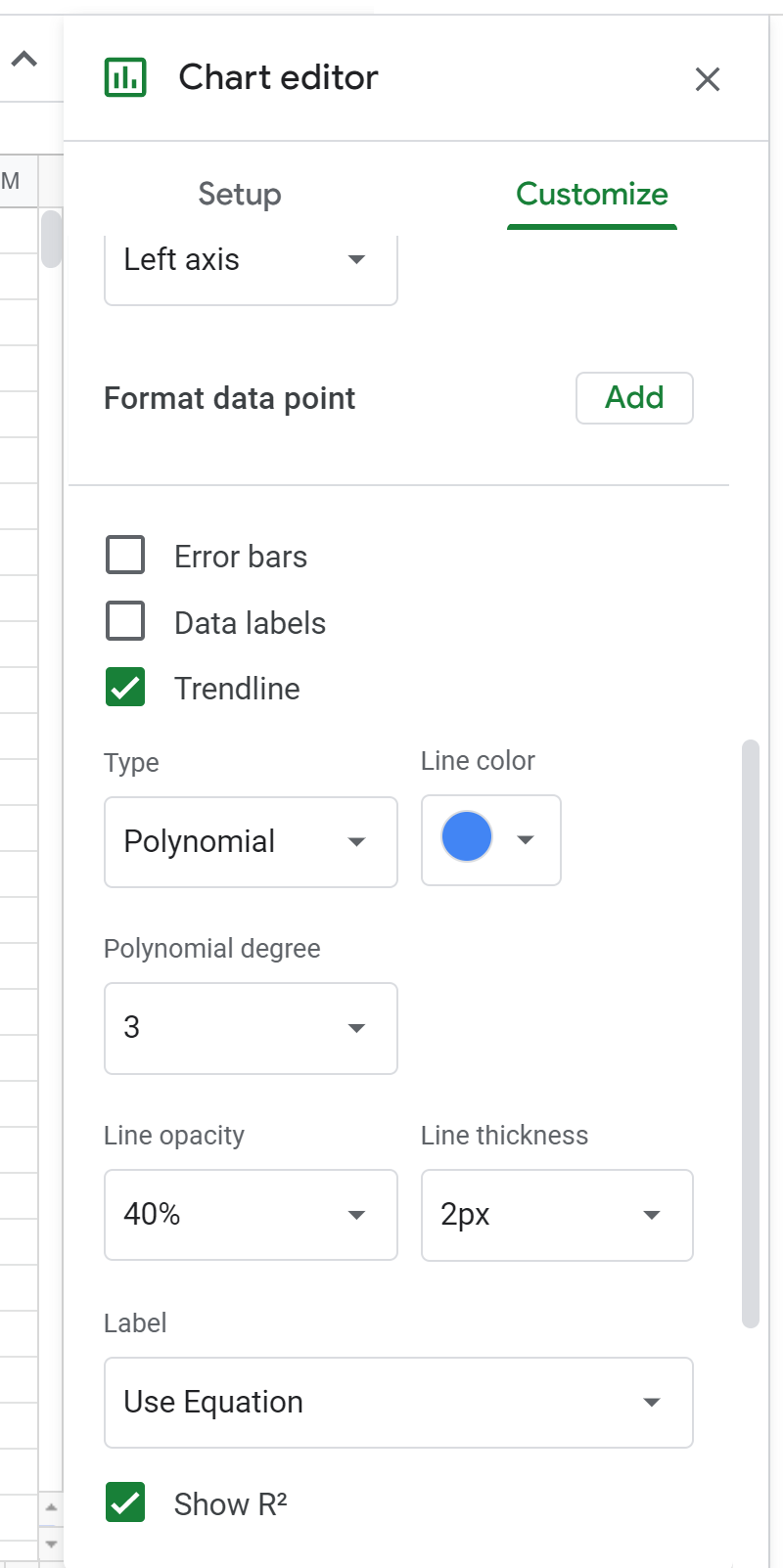
그러면 산점도 위에 다음 공식이 표시됩니다.

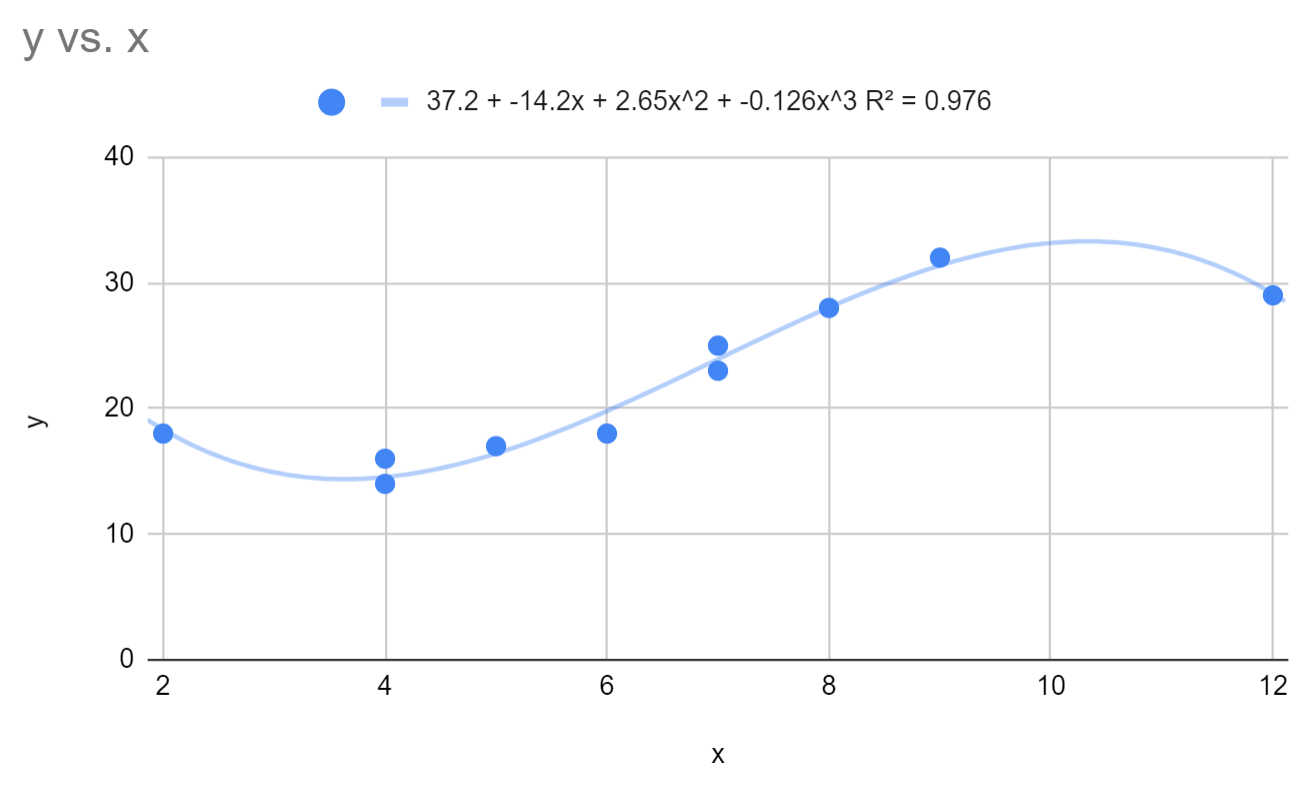
그러면 적합 다항식 회귀 방정식이 다음과 같이 변경됩니다.

y = 37.2 – 14.2x + 2.64x ² – 0.126x ³

이 모델의 R 제곱은 0.976 입니다.

이 모델의 R-제곱은 차수가 2인 다항식 회귀 모델보다 상당히 높습니다. 이는 이 회귀 모델이 기본 데이터의 추세를 포착하는 데 훨씬 더 우수하다는 것을 의미합니다.

다항식의 차수를 4로 변경하면 R 제곱은 거의 0.981 로 증가하지 않습니다. 이는 3차 다항식 회귀 모델이 이러한 데이터의 추세를 포착하는 데 충분하다는 것을 의미합니다.

적합 회귀 방정식을 사용하여 주어진 예측 변수 값에 대해 응답 변수의 기대 값을 찾을 수 있습니다. 예를 들어 x = 4인 경우 y 의 예상 값은 다음과 같습니다.

y = 37.2 – 14.2(4) + 2.64(4) ² – 0.126(4) ³ = 14.576

이 페이지 에서 다른 Google 스프레드시트 튜토리얼을 찾을 수 있습니다.