R의 다항식 회귀(단계별)

다항식 회귀는 예측 변수와 응답 변수 간의 관계가 비선형일 때 사용할 수 있는 기술입니다.

이러한 유형의 회귀는 다음과 같은 형식을 취합니다.

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _h

여기서 h 는 다항식의 “차수”입니다.

이 튜토리얼에서는 R에서 다항식 회귀를 수행하는 방법에 대한 단계별 예를 제공합니다.

1단계: 데이터 생성

이 예에서는 학생 50명에 대한 학습 시간과 최종 시험 성적이 포함된 데이터 세트를 만듭니다.

 #make this example reproducible
set.seed(1)

#create dataset
df <- data.frame(hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(data)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

2단계: 데이터 시각화

회귀 모델을 데이터에 맞추기 전에 먼저 공부 시간과 시험 점수 사이의 관계를 시각화하는 산점도를 만들어 보겠습니다.

 library (ggplot2)

ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

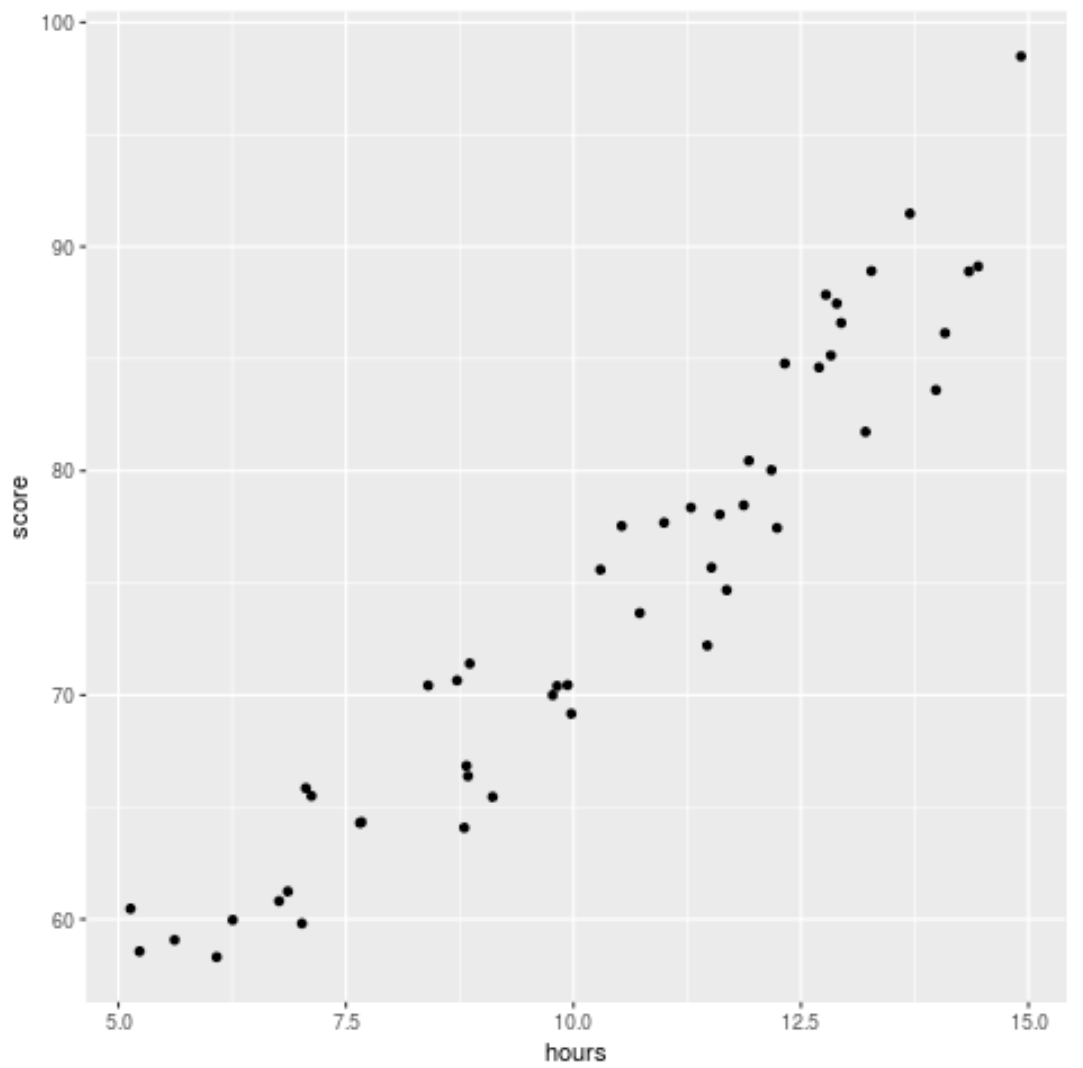
데이터에 약간의 2차 관계가 있다는 것을 알 수 있는데, 이는 다항식 회귀가 단순 선형 회귀보다 데이터에 더 잘 맞을 수 있음을 나타냅니다.

3단계: 다항 회귀 모델 피팅

다음으로, 차수 h = 1…5인 5개의 서로 다른 다항식 회귀 모델을 피팅하고 k = 10번으로 k겹 교차 검증을 사용하여 각 모델에 대한 MSE 테스트를 계산합니다.

 #randomly shuffle data
df.shuffled <- df[ sample ( nrow (df)),]

#define number of folds to use for k-fold cross-validation
K <- 10 

#define degree of polynomials to fit
degree <- 5

#create k equal-sized folds
folds <- cut( seq (1, nrow (df.shuffled)), breaks=K, labels= FALSE )

#create object to hold MSE's of models
mse = matrix(data=NA,nrow=K,ncol=degree)

#Perform K-fold cross validation
for (i in 1:K){
    
#define training and testing data
testIndexes <- which (folds==i,arr.ind= TRUE )
    testData <- df.shuffled[testIndexes, ]
    trainData <- df.shuffled[-testIndexes, ]
    
#use k-fold cv to evaluate models
for (j in 1:degree){
        fit.train = lm (score ~ poly (hours,d), data=trainData)
        fit.test = predict (fit.train, newdata=testData)
        mse[i,j] = mean ((fit.test-testData$score)^2) 
    }
}

#find MSE for each degree 
colMeans(mse)

[1] 9.802397 8.748666 9.601865 10.592569 13.545547

결과에서 각 모델에 대한 MSE 테스트를 볼 수 있습니다.

• h = 1인 MSE 테스트: 9.80
• h = 2인 MSE 테스트: 8.75
• h = 3인 MSE 테스트: 9.60
• h = 4인 MSE 테스트: 10.59
• h = 5인 MSE 테스트: 13.55

테스트 MSE가 가장 낮은 모델은 차수 h = 2인 다항식 회귀 모델로 나타났습니다.

이는 원래 산점도의 직관과 일치합니다. 즉, 2차 회귀 모델이 데이터에 가장 적합합니다.

4단계: 최종 모델 분석

마지막으로, 가장 성능이 좋은 모델의 계수를 얻을 수 있습니다.

 #fit best model
best = lm (score ~ poly (hours,2, raw= T ), data=df)

#view summary of best model
summary(best)

Call:
lm(formula = score ~ poly(hours, 2, raw = T), data = df)

Residuals:
    Min 1Q Median 3Q Max 
-5.6589 -2.0770 -0.4599 2.5923 4.5122 

Coefficients:
                         Estimate Std. Error t value Pr(>|t|)    
(Intercept) 54.00526 5.52855 9.768 6.78e-13 ***
poly(hours, 2, raw = T)1 -0.07904 1.15413 -0.068 0.94569    
poly(hours, 2, raw = T)2 0.18596 0.05724 3.249 0.00214 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

결과에서 최종 적합 모델은 다음과 같습니다.

점수 = 54.00526 – 0.07904*(시간) + 0.18596*(시간) ²

이 방정식을 사용하여 학생이 공부한 시간을 기준으로 받게 될 점수를 추정할 수 있습니다.

예를 들어, 10시간 공부한 학생은 71.81 점을 받아야 합니다.

점수 = 54.00526 – 0.07904*(10) + 0.18596*(10) ² = 71.81

또한 피팅된 모델을 플롯하여 원시 데이터에 얼마나 잘 맞는지 확인할 수도 있습니다.

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

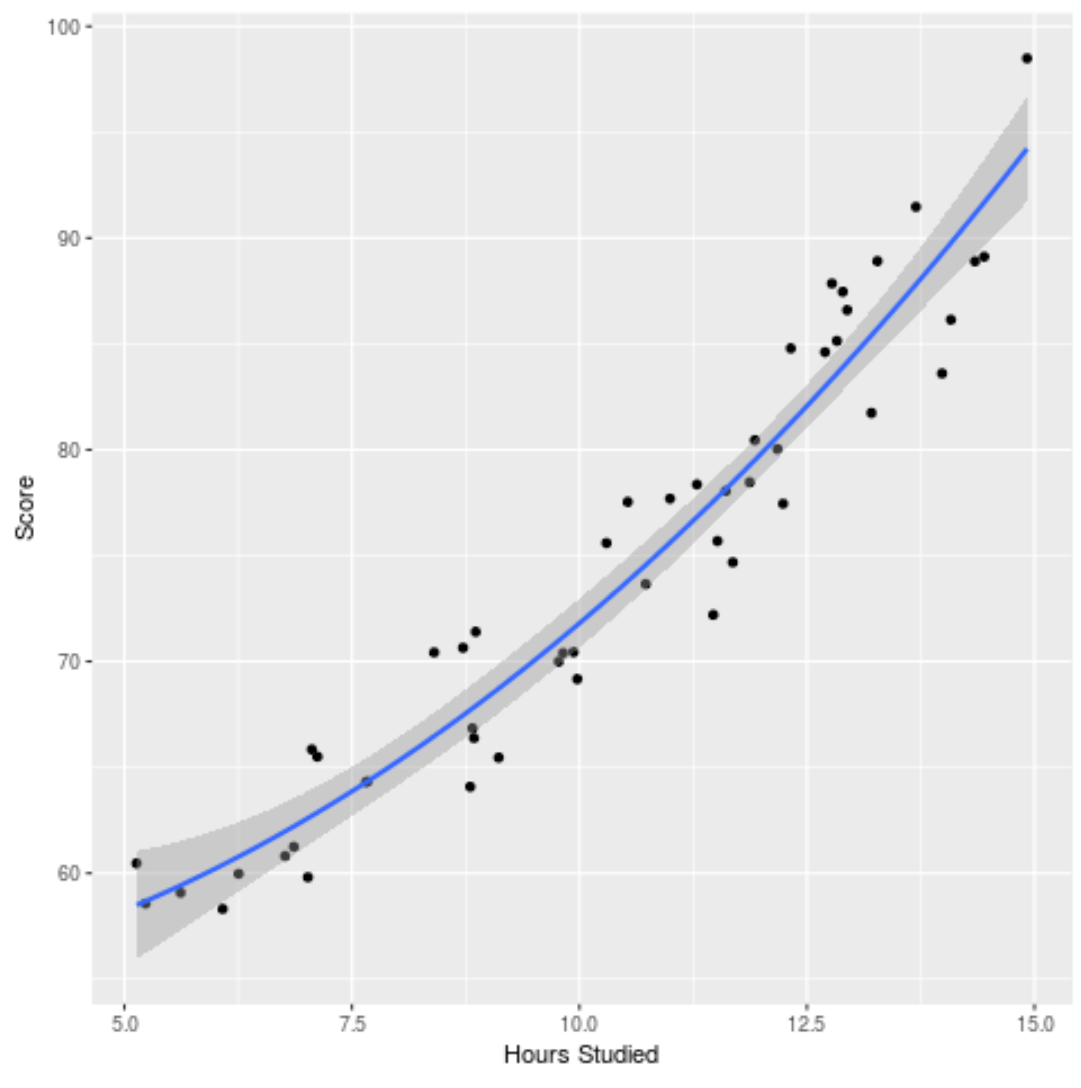
이 예제에 사용된 전체 R 코드는 여기에서 찾을 수 있습니다.