Spss에서 일원 분산 분석을 수행하는 방법

일원 분산 분석은 3개 이상의 독립 그룹 평균 간에 통계적으로 유의한 차이가 있는지 여부를 확인하는 데 사용됩니다.

이러한 유형의 테스트는 예측 변수가 반응 변수에 미치는 영향을 분석하기 때문에 일원 분산 분석이라고 합니다.

대신 두 예측 변수가 반응 변수에 미치는 영향에 관심이 있다면 양방향 ANOVA를 수행할 수 있습니다.

이 튜토리얼에서는 SPSS에서 일원 분산 분석을 수행하는 방법을 설명합니다.

예: SPSS의 일원 분산 분석

한 연구자가 연구에 참여할 학생 30명을 모집한다고 가정해 보겠습니다. 학생들은 시험 준비를 위해 다음 달에 세 가지 학습 방법 중 하나를 사용하도록 무작위로 배정됩니다. 월말에는 모든 학생들이 동일한 시험을 치릅니다.

학생 테스트 결과는 다음과 같습니다.

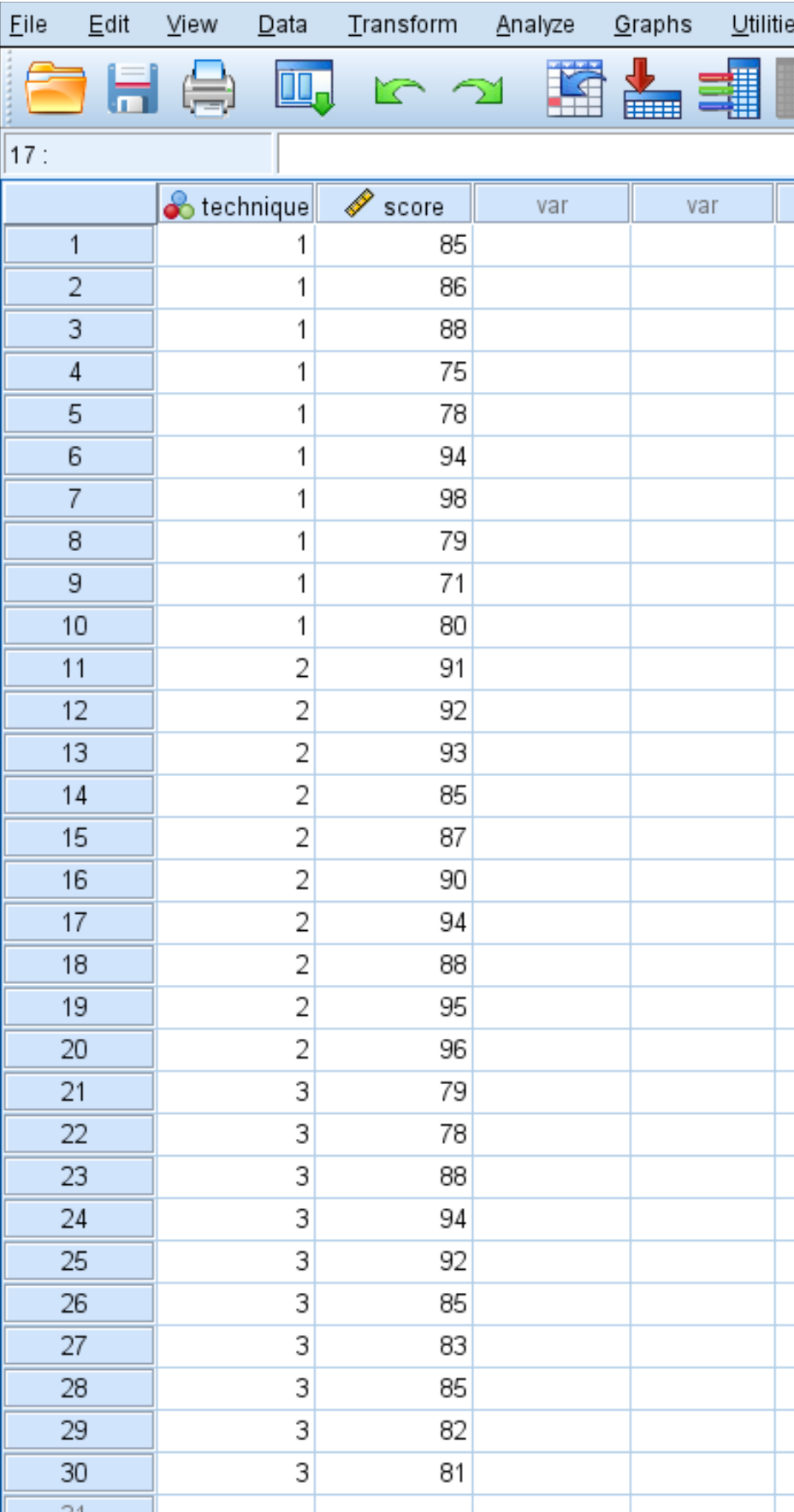
다음 단계를 사용하여 일원 분산 분석을 수행하여 세 그룹의 평균 점수가 동일한지 확인합니다.

1단계: 데이터를 시각화합니다.

먼저 세 가지 학습 기법 각각에 대한 시험 점수 분포를 시각화하기 위해상자 그림을 만듭니다. 차트 탭을 클릭한 다음 차트 작성기 를 클릭합니다.

다음에서 선택: 창에서 상자 그림을 선택합니다. 그런 다음 Simple boxplot 이라고 표시된 첫 번째 차트를 기본 편집 창으로 드래그합니다. x축에 기술 변수를 끌어 놓고 y축에 점수를 끌어 놓습니다.

그런 다음 요소 속성 을 클릭하고 Y1 축 을 클릭합니다 . 최소값 을 60으로 변경합니다. 그런 다음 확인을 클릭합니다.

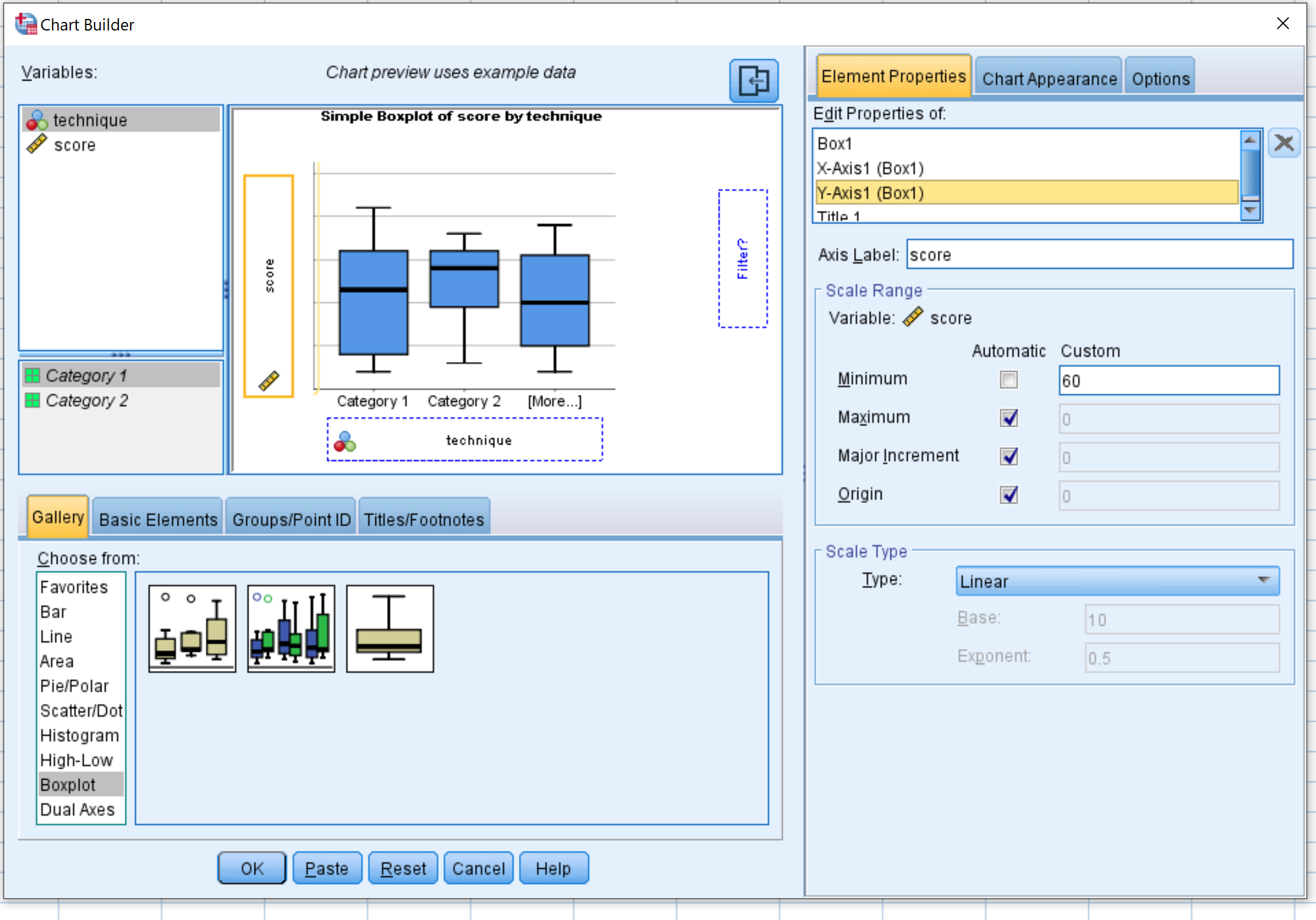
다음 상자 그림이 나타납니다.

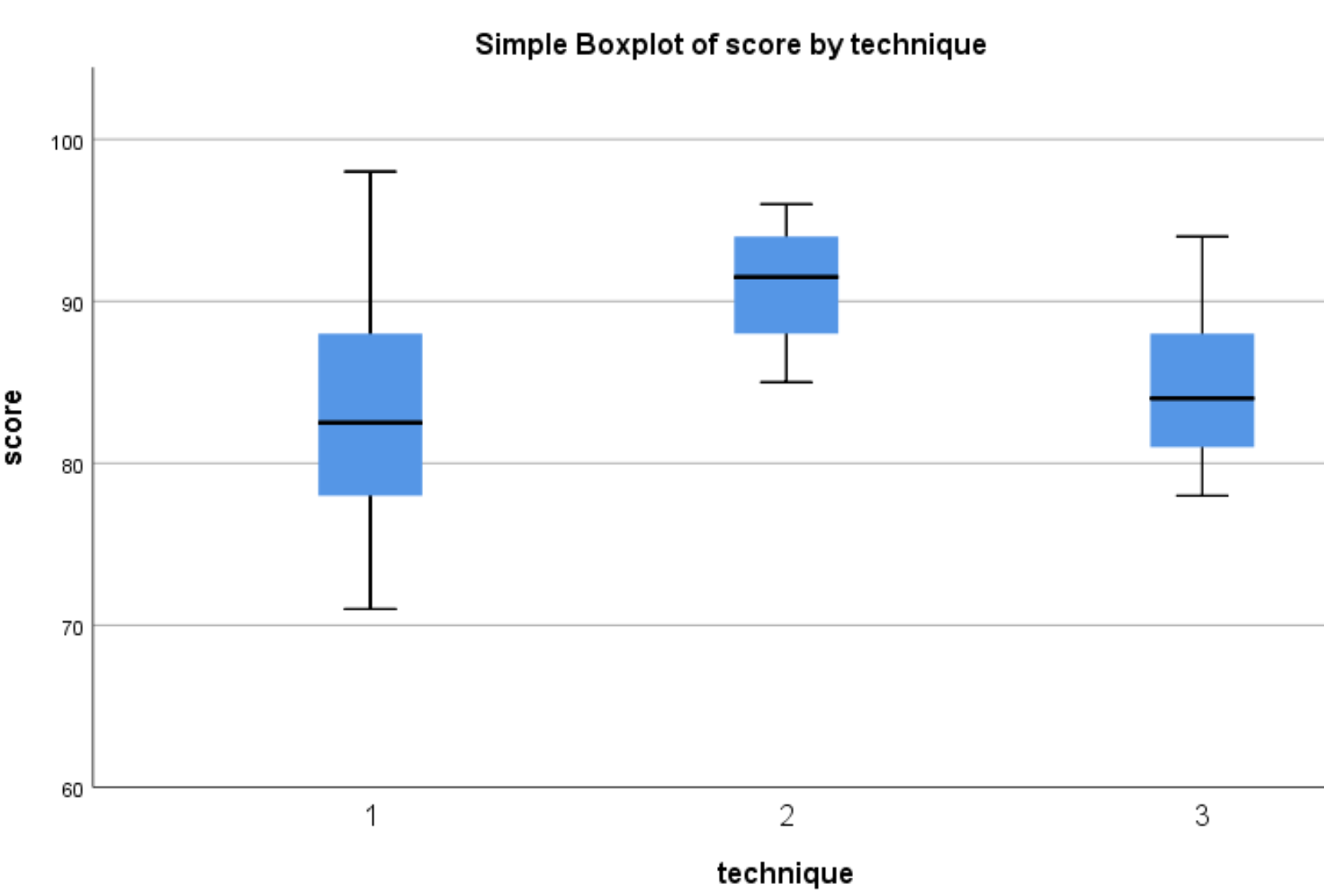
기술 1과 3을 사용한 학생보다 기술 2를 사용한 학생의 시험 점수 분포가 더 높은 경향이 있음을 알 수 있습니다. 이러한 점수 차이가 통계적으로 유의한지 여부를 확인하기 위해 일원 분산 분석을 수행합니다.

2단계: 일원 분산 분석을 수행합니다.

분석 탭을 클릭한 다음 평균 비교 , 일원 분산 분석을 차례로 클릭합니다.

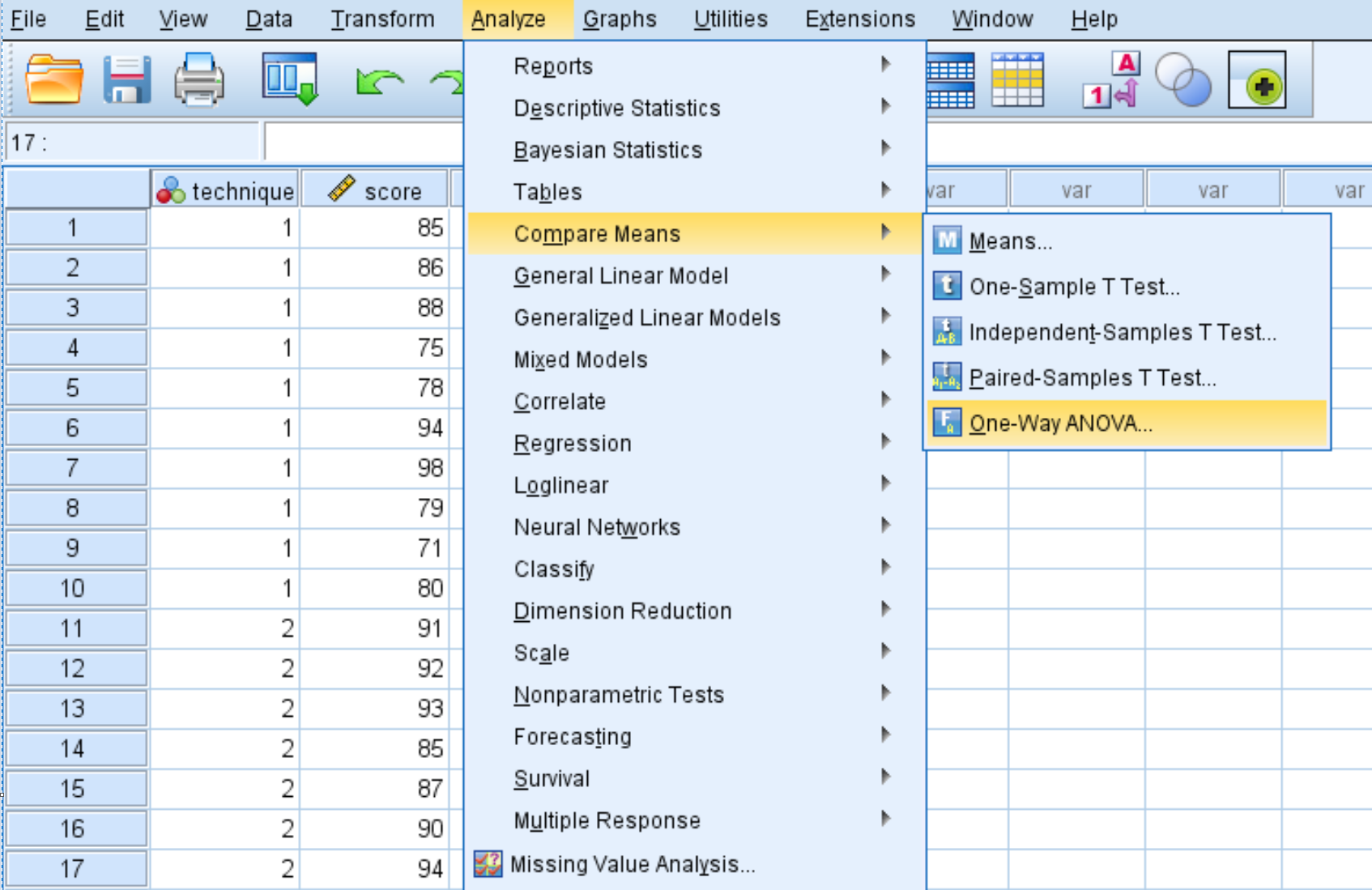
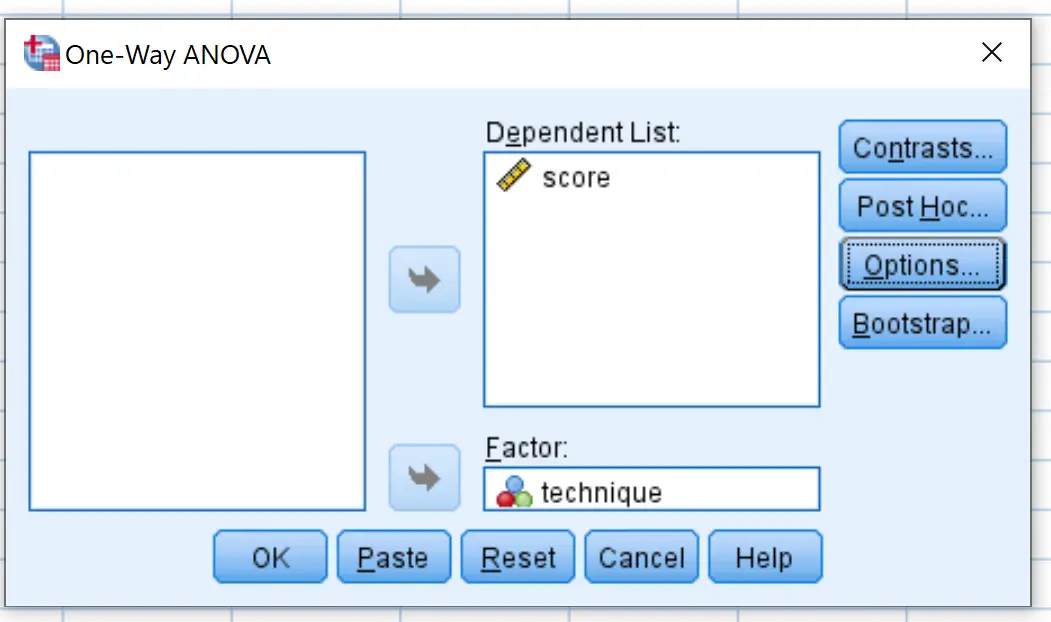
나타나는 새 창에서 종속 목록 상자에 변수 점수를 배치하고 요인 상자에 변수 기술을 배치합니다.

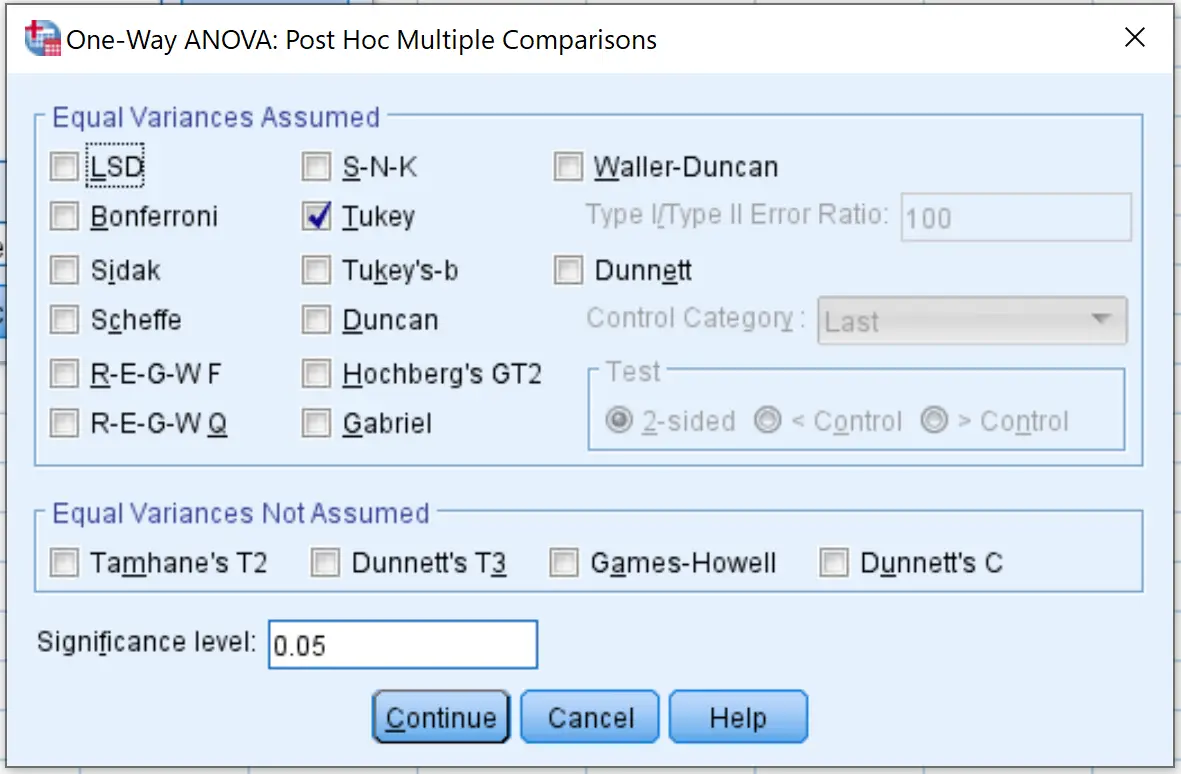
그런 다음 사후관리를 클릭하고 Tukey 옆의 확인란을 선택합니다. 그런 다음 계속 을 클릭합니다.

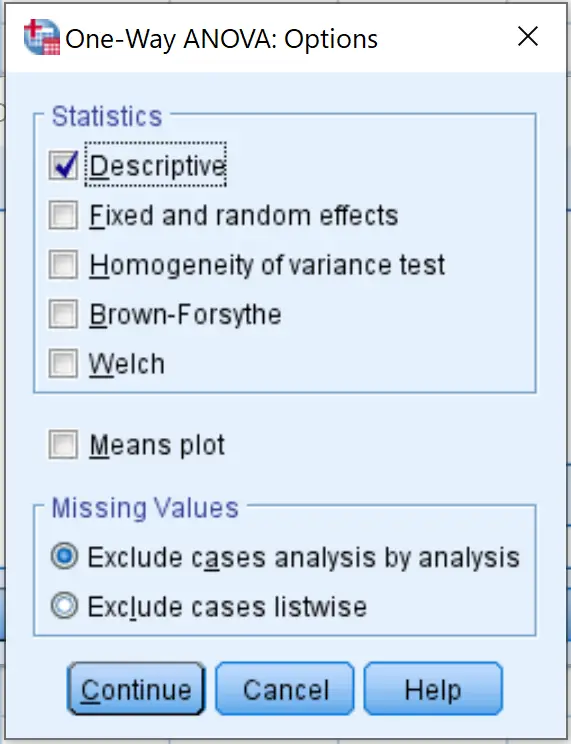
그런 다음 옵션을 클릭하고 설명 옆의 확인란을 선택합니다. 그런 다음 계속 을 클릭합니다.

마지막으로 확인 을 클릭합니다.

3단계: 결과를 해석합니다.

확인을 클릭하면 일원 분산 분석 결과가 나타납니다. 결과를 해석하는 방법은 다음과 같습니다.

테이블 설명

이 표에는 데이터 세트의 세 그룹 각각에 대한 기술 통계가 표시됩니다.

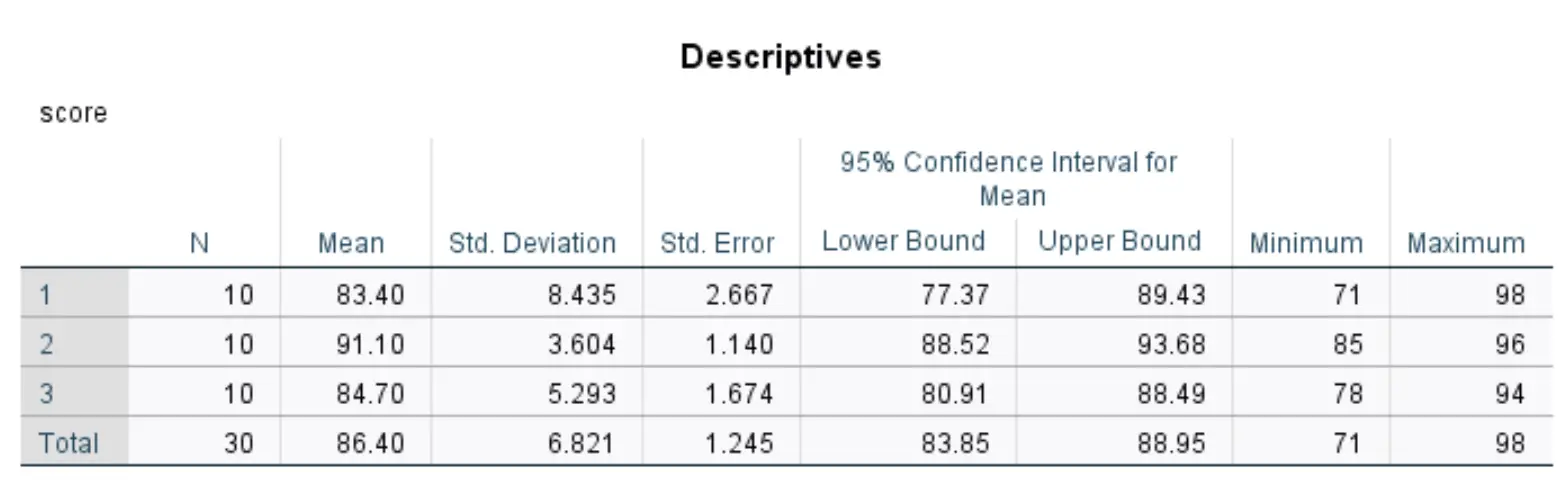
가장 관련성이 높은 수치는 다음과 같습니다.

• N: 각 그룹의 학생 수입니다.
• 평균: 각 그룹의 평균 시험 점수입니다.
• 기준. 편차: 각 그룹에 대한 테스트 결과의 표준 편차입니다.

분산분석표

이 표는 일원 분산 분석의 결과를 표시합니다.

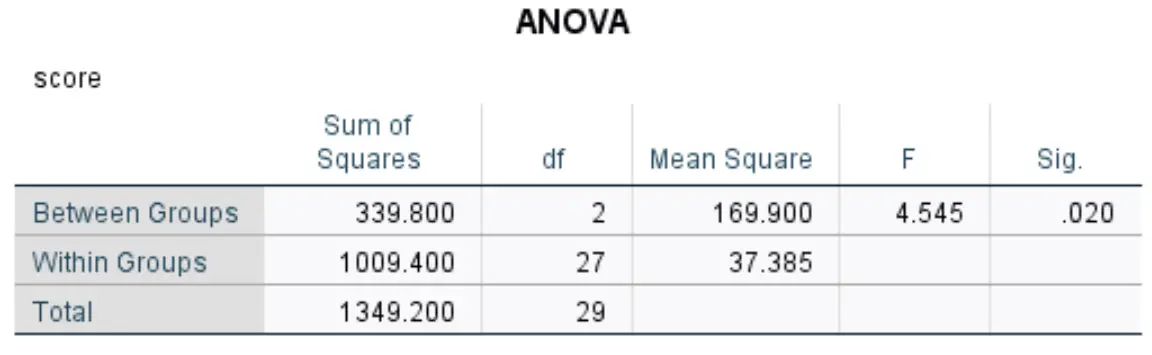
가장 관련성이 높은 수치는 다음과 같습니다.

• F: 전체 F 통계입니다.
• Sig: 분자가 df(2)이고 분모가 df(27)인 F 통계(4.545)에 해당하는 p-값입니다. 이 경우 p-값은 0.020 으로 나타납니다.

일원 분산 분석에서는 다음과 같은 귀무 가설과 대립 가설을 사용합니다.

• H ₀ (귀무가설): μ ₁ = μ ₂ = μ ₃ = … = μ _k (모든 모집단 평균이 동일함)
• _HA (대립가설): 적어도 하나의 모집단 평균이 다릅니다.   나머지

ANOVA 테이블의 p-값이 0.05보다 작기 때문에 귀무 가설을 기각하고 그룹 평균 중 하나 이상이 다른 평균과 다르다는 결론을 내릴 수 있는 충분한 증거가 있습니다.

어떤 그룹의 평균이 서로 다른지 정확히 알기 위해 ANOVA 결과의 마지막 표를 참조할 수 있습니다.

다중 비교표

이 표는 세 그룹 각각에 대한 Tukey의 사후 다중 비교를 표시합니다. 우리는 주로 Sig에 관심이 있습니다. 각 그룹 간의 평균 차이에 대한 p-값을 표시하는 열:

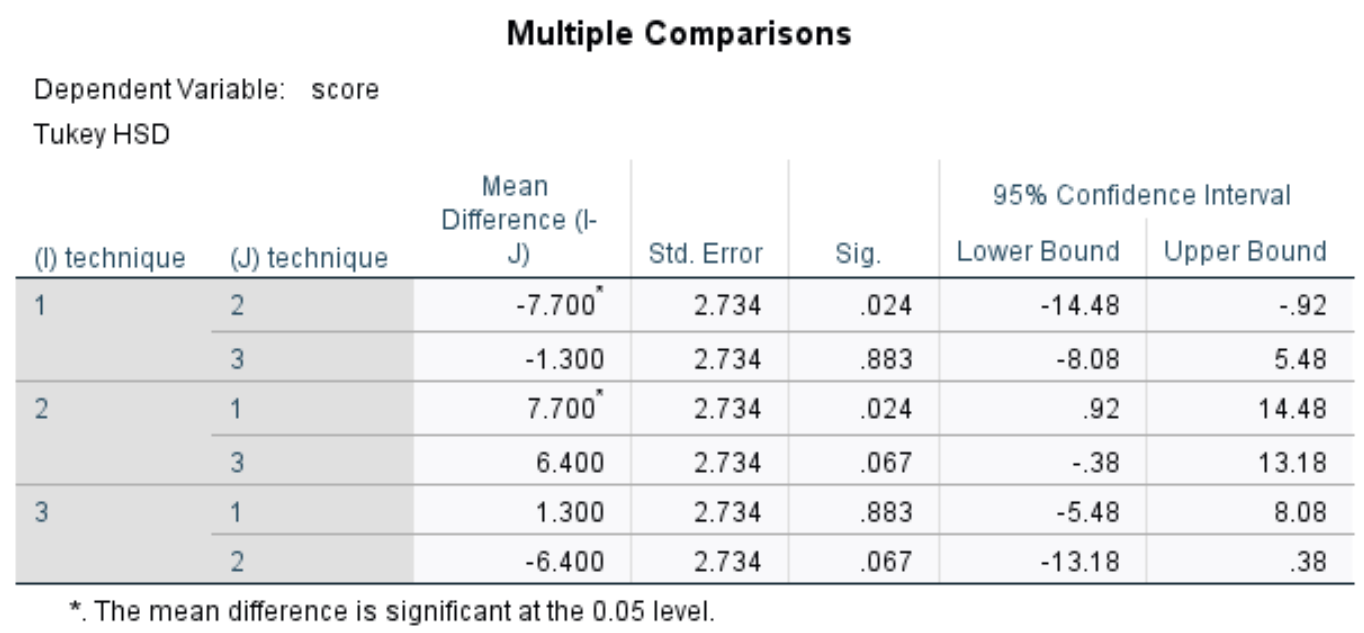
표에서 다음 비교에 대한 p-값을 볼 수 있습니다.

• 2에 대한 기술 1: | p-값 = 0.024
• 3에 대한 기술 1 | p-값 = 0.883
• 3에 대한 기술 2 | p-값 = 0.067

p-값이 0.05보다 작은 유일한 그룹 비교는 기술 1과 기술 2 사이입니다.

이는 기법 1을 사용한 학생과 기법 2를 사용한 학생 사이의 평균 시험 점수에 통계적으로 유의한 차이가 있음을 말해줍니다.

그러나 기술 1과 3 사이, 기술 2와 3 사이에는 통계적으로 유의미한 차이가 없습니다.

4단계: 결과를 보고합니다.

마지막으로 일원 분산 분석(one-way ANOVA) 결과를 보고할 수 있습니다. 이를 수행하는 방법의 예는 다음과 같습니다.

세 가지 서로 다른 연구 기법으로 인해 서로 다른 테스트 결과가 발생하는지 여부를 확인하기 위해 일원 분산 분석(one-way ANOVA)이 수행되었습니다.

총 10명의 학생이 모두 동일한 시험을 치르기 전에 한 달 동안 세 가지 학습 방법을 각각 사용했습니다.

일원 분산 분석(one-way ANOVA)을 통해 적어도 두 그룹 간의 시험 점수에 통계적으로 유의한 차이가 있는 것으로 나타났습니다(F(2, 27) = 4.545, p = 0.020).

다중 비교를 위한 Tukey 테스트에서는 기법 1과 기법 2를 사용한 학생들 사이의 평균 시험 점수가 유의하게 다른 것으로 나타났습니다(p = 0.024, 95% CI = [-14.48, -0.92]).

기술 1과 3의 점수(p = 0.883) 또는 기술 2와 3의 점수(p = 0.067) 사이에는 통계적으로 유의미한 차이가 없었습니다.