일원 분산 분석: 정의, 공식 및 예
일원 분산 분석 (“분산 분석”)은 3개 이상의 독립 그룹의 평균을 비교하여 해당 모집단의 평균 간에 통계적으로 유의미한 차이가 있는지 확인합니다.
이 튜토리얼에서는 다음 내용을 설명합니다.
- 일원 분산 분석을 수행하려는 동기.
- 일원 분산 분석을 수행하기 위해 충족되어야 하는 가정입니다.
- 일원 분산 분석을 수행하는 프로세스입니다.
- 일원 분산 분석을 수행하는 방법의 예입니다.
일원 분산 분석: 동기 부여
세 가지 다른 시험 준비 프로그램으로 인해 대학 입학 시험에서 평균 점수가 달라지는지 여부를 알고 싶다고 가정해 보겠습니다. 전국에 수백만 명의 고등학생이 있기 때문에 모든 학생에게 시험 준비 프로그램 중 하나를 사용하게 하는 것은 너무 많은 시간과 비용이 소요됩니다.
대신, 우리는 모집단에서 100명의 학생 중 무작위 표본 3개를 선택하고 각 표본이 세 가지 시험 준비 프로그램 중 하나를 사용하여 시험을 준비하도록 할 수 있습니다. 그런 다음 각 학생이 시험에 응시한 후 점수를 기록할 수 있습니다.
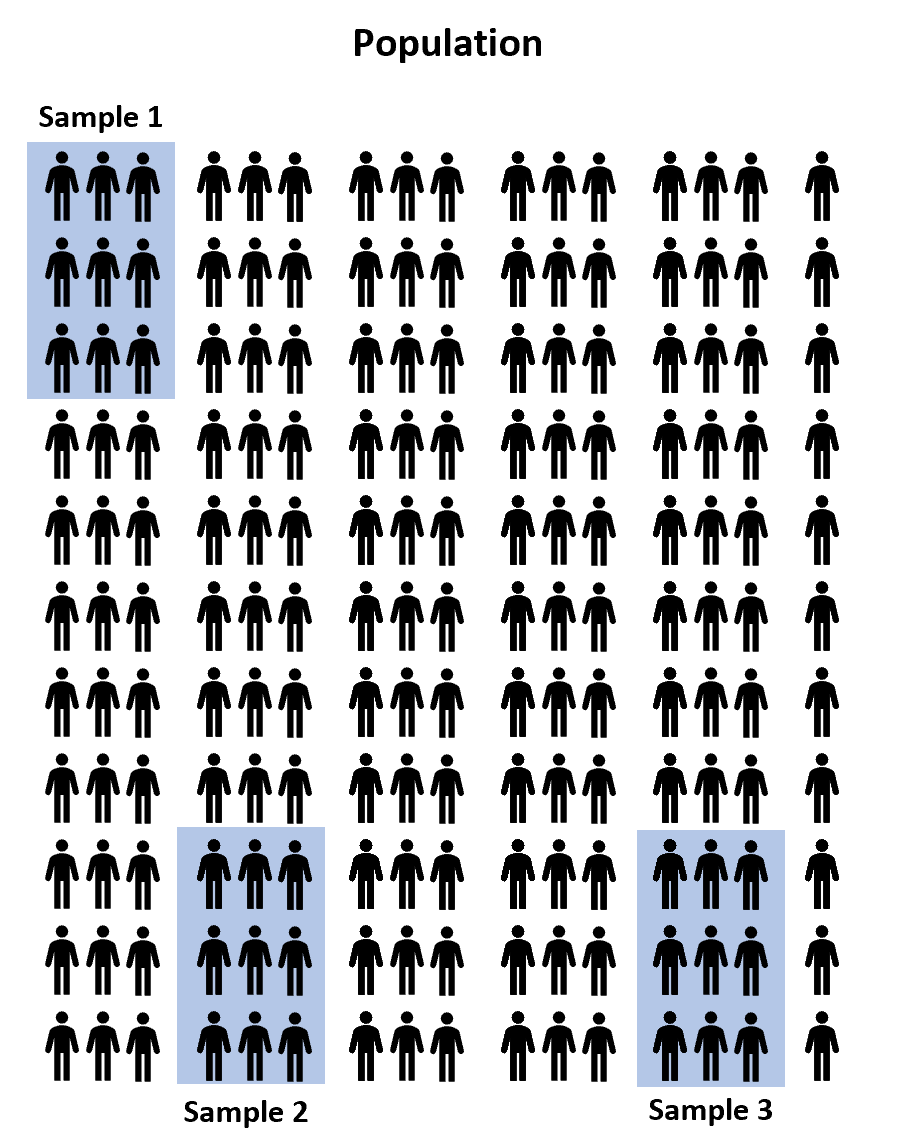
그러나 세 샘플 간의 평균 시험 점수는 최소한 약간씩 다를 것이라는 것은 사실상 보장됩니다. 문제는 이 차이가 통계적으로 유의한지 여부입니다 . 다행히도 일원 분산 분석을 통해 이 질문에 답할 수 있습니다.
일원 분산 분석: 가정
일원 분산 분석의 결과가 유효하려면 다음 가정이 충족되어야 합니다.
1. 정규성 – 각 표본은 정규 분포 모집단에서 추출되었습니다.
2. 등분산 – 표본을 추출하는 모집단의 분산이 동일합니다. Bartlett의 검정을 사용하여 이 가설을 검정할 수 있습니다.
3. 독립성 – 각 그룹 내의 관측치는 서로 독립적이며 그룹 내의 관측치는 무작위 샘플링을 통해 얻어졌습니다.
이러한 가정을 확인하는 방법에 대한 자세한 내용은 이 문서를 읽어보세요.
일원 분산 분석: 프로세스
일원 분산 분석에서는 다음과 같은 귀무 가설과 대립 가설을 사용합니다.
- H 0 (귀무가설): μ 1 = μ 2 = μ 3 = … = μ k (모든 모집단 평균이 동일함)
- H 1 (대립 가설): 적어도 하나의 모집단 평균이 다릅니다. 나머지
일원 분산 분석은 수동으로 수행하는 것이 지루하기 때문에 일반적으로 일부 통계 소프트웨어(예: R, Excel, Stata, SPSS 등)를 사용하여 일원 분산 분석을 수행합니다.
사용하는 소프트웨어에 관계없이 다음 표가 출력으로 표시됩니다.
| 원천 | 제곱합(SS) | df | 평균 제곱(MS) | 에프 | 피 |
|---|---|---|---|---|---|
| 치료 | RSS | df r | MSR | MSR/MSE | F df r , df e |
| 오류 | ESS | df e | MSE | ||
| 총 | OHS | df t |
금:
- SSR: 제곱합 회귀
- SSE: 제곱 오차의 합
- SST: 총 제곱합(SST = SSR + SSE)
- df r : 회귀 자유도(df r = k-1)
- df e : 오차 자유도(df e = nk)
- df t : 총 자유도 (df t = n-1)
- k: 총 그룹 수
- n: 총 관측치
- MSR: 평균 제곱 회귀(MSR = SSR/df r )
- MSE: 평균 제곱 오차(MSE = SSE/df e )
- F: F 검정 통계량(F = MSR/MSE)
- p: F dfr, dfe 에 해당하는 값 p
p-값이 선택한 유의 수준(예: 0.05)보다 작은 경우 귀무 가설을 기각하고 모집단 평균 중 하나 이상이 다른 평균과 다르다는 결론을 내릴 수 있습니다.
참고: 귀무 가설을 기각하는 경우 이는 모집단 평균 중 하나 이상이 다른 모집단 평균과 다르다는 것을 의미하지만 분산 분석표에서는 어떤 모집단 평균이 다른지 지정하지 않습니다. 이를 확인하려면 “다중 비교” 테스트라고도 하는 사후 테스트를 수행해야 합니다.
일원 분산 분석: 예
세 가지 서로 다른 시험 준비 프로그램이 특정 시험에서 서로 다른 평균 점수를 가져오는지 여부를 알고 싶다고 가정해 보겠습니다. 이를 테스트하기 위해 우리는 연구에 참여할 학생 30명을 모집하고 그들을 세 그룹으로 나눕니다.
각 그룹의 학생들은 시험 준비를 위해 다음 3주 동안 세 가지 시험 준비 프로그램 중 하나를 사용하도록 무작위로 배정 됩니다. 3주 후에는 모든 학생들이 동일한 시험을 치릅니다.
각 그룹의 시험 결과는 다음과 같습니다.

이 데이터에 대해 일원 분산 분석을 수행하기 위해 다음 입력과 함께 통계 일원 분산 분석 계산기를 사용합니다.

출력 테이블에서 F 검정 통계량은 2.358 이고 해당 p-값은 0.11385 임을 알 수 있습니다.

이 p-값은 0.05 이상이므로 귀무가설을 기각할 수 없습니다.
이는 세 그룹의 평균 시험 점수 간에 통계적으로 유의미한 차이가 있다고 말할 수 있는 충분한 증거가 없음을 의미합니다.
추가 리소스
다음 문서에서는 다양한 통계 소프트웨어를 사용하여 일원 분산 분석을 수행하는 방법을 설명합니다.
Excel에서 일원 분산 분석을 수행하는 방법
R에서 일원 분산 분석을 수행하는 방법
Python에서 일원 분산 분석을 수행하는 방법
SAS에서 일원 분산 분석을 수행하는 방법
SPSS에서 일원 분산 분석을 수행하는 방법
Stata에서 일원 분산 분석을 수행하는 방법
TI-84 계산기에서 일원 분산 분석을 수행하는 방법
온라인 일원 분산 분석 계산기