Stata에서 단순 선형 회귀를 수행하는 방법

단순 선형 회귀는 설명 변수 x와 응답 변수 y 사이의 관계를 이해하는 데 사용할 수 있는 방법입니다.

이 튜토리얼에서는 Stata에서 간단한 선형 회귀를 수행하는 방법을 설명합니다.

예: Stata의 단순 선형 회귀

자동차의 무게와 갤런당 마일 사이의 관계를 이해하고 싶다고 가정해 보겠습니다. 이 관계를 탐색하기 위해 설명 변수로 무게를 사용하고 응답 변수로 갤런당 마일을 사용하여 간단한 선형 회귀를 수행할 수 있습니다.

74개의 서로 다른 자동차에 대한 데이터가 포함된 auto 라는 데이터 세트를 사용하여 간단한 선형 회귀를 수행하려면 Stata에서 다음 단계를 완료하세요.

1단계: 데이터를 로드합니다.

명령 상자에 다음을 입력하여 데이터를 로드합니다.

https://www.stata-press.com/data/r13/auto를 사용하세요.

2단계: 데이터 요약을 가져옵니다.

명령 상자에 다음을 입력하여 작업 중인 데이터를 빠르게 이해하세요.

요약

데이터세트에 12개의 서로 다른 변수가 있다는 것을 알 수 있지만 우리가 관심을 갖는 두 가지 변수는 mpg 와 Weight 뿐입니다.

3단계: 데이터를 시각화합니다.

단순 선형 회귀를 수행하기 전에 먼저 무게 대 mpg의 산점도를 만들어 이 두 변수 간의 관계를 시각화하고 명백한 이상값을 확인하겠습니다. 산점도를 생성하려면 명령 상자에 다음을 입력합니다.

mpg 무게 분산

그러면 다음과 같은 산점도가 생성됩니다.

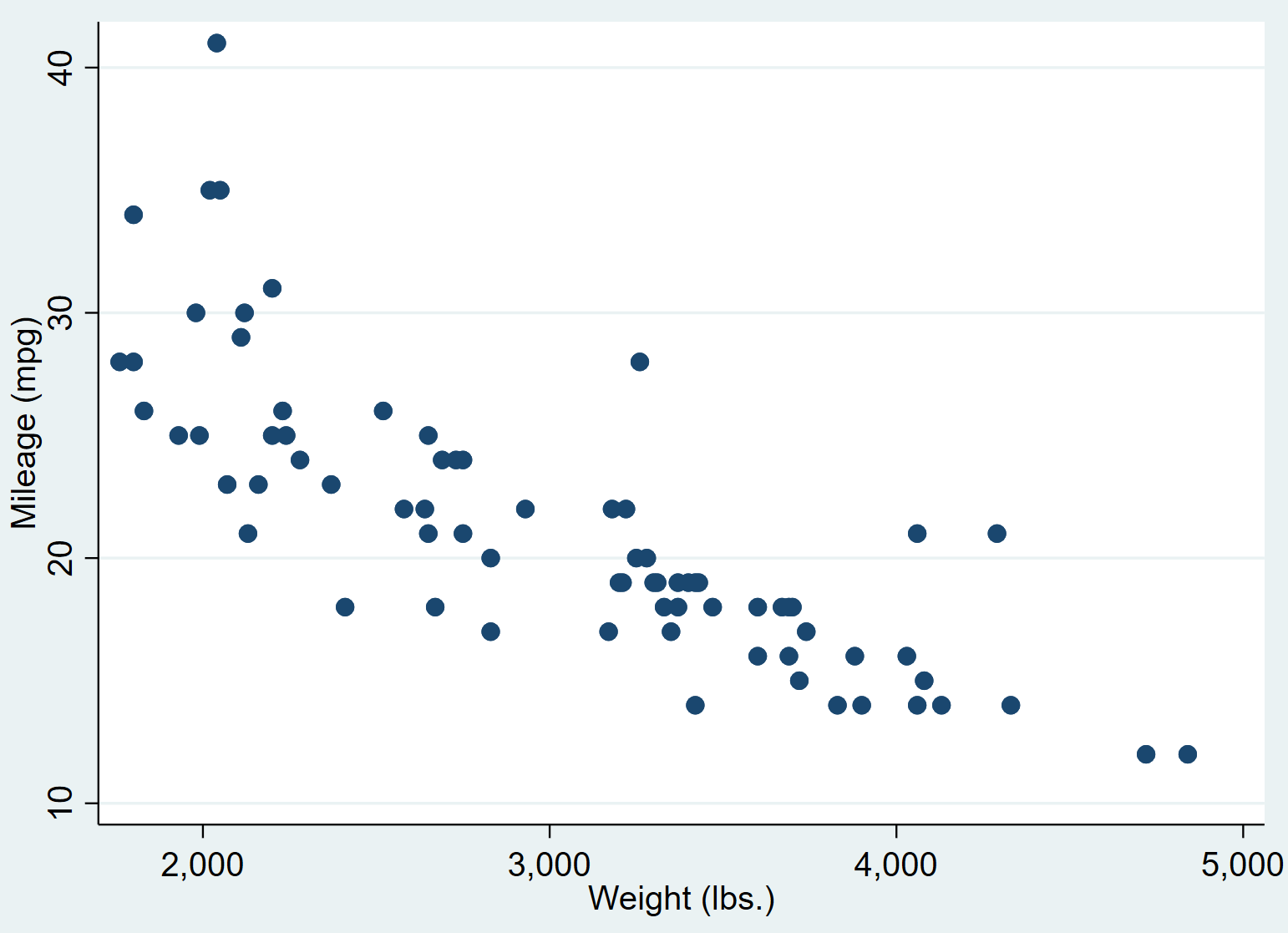
중량이 더 높은 자동차의 경우 갤런당 마일이 더 적은 경향이 있음을 알 수 있습니다. 이 관계를 정량화하기 위해 이제 간단한 선형 회귀를 수행하겠습니다.

4단계: 단순 선형 회귀를 수행합니다.

설명 변수로 무게를 사용하고 응답 변수로 mpg를 사용하여 단순 선형 회귀를 수행하려면 명령 상자에 다음을 입력합니다.

체중을 mpg로 회귀

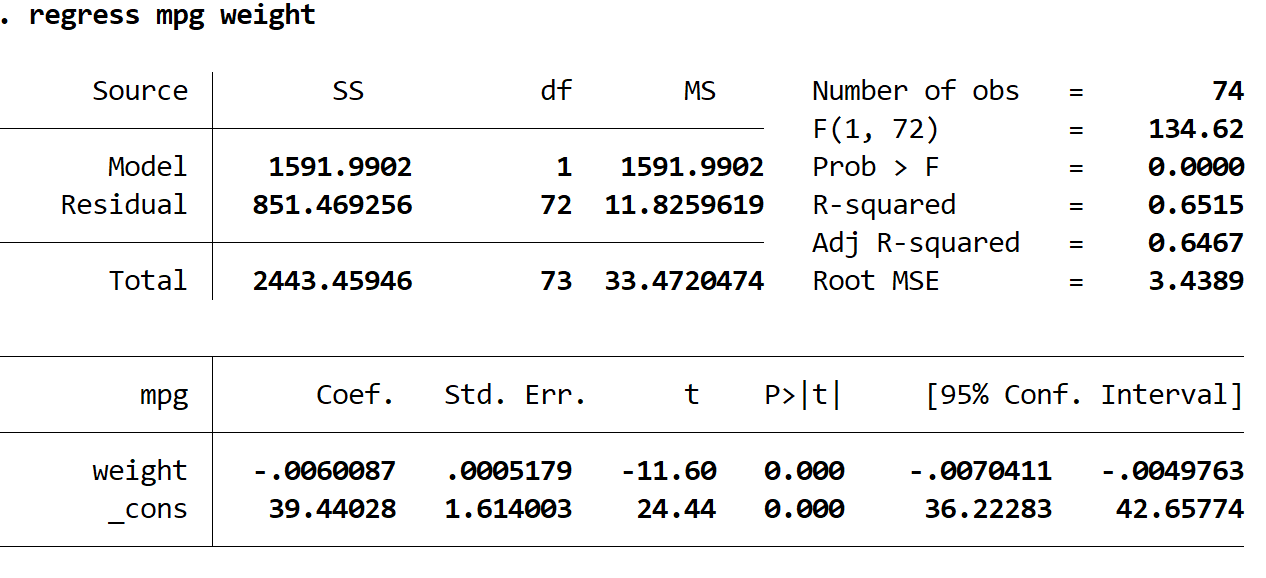
결과에서 가장 흥미로운 숫자를 해석하는 방법은 다음과 같습니다.

R 제곱: 0.6515. 이는 설명 변수로 설명할 수 있는 반응 변수의 분산 비율입니다. 이 예에서는 mpg 변화의 65.15%가 중량으로 설명될 수 있습니다.

계수(무게): -0.006. 이는 설명 변수의 1단위 증가와 관련된 반응 변수의 평균 변화를 알려줍니다. 이 예에서 체중이 1파운드 증가할 때마다 평균 0.006mpg가 감소합니다.

계수(_cons): 39.44028. 이는 설명변수가 0일 때 반응변수의 평균값을 알려줍니다. 이 예에서 자동차 중량이 0일 때 평균 mpg는 39.44028입니다. 자동차의 무게는 0이 될 수 없으므로 해석하는 것이 실제로 의미가 없지만 회귀 방정식을 구성하려면 숫자 39.44028이 필요합니다.

피>|티| (무게): 0.000. 이는 체중에 대한 검정 통계량과 연관된 p-값입니다. 이 경우 이 값이 0.05보다 작으므로 체중과 mpg 사이에 통계적으로 유의한 관계가 있다고 결론을 내릴 수 있습니다.

회귀 방정식: 마지막으로 두 계수 값을 사용하여 회귀 방정식을 구성할 수 있습니다. 이 경우 방정식은 다음과 같습니다.

예상 mpg = 39.44028 – 0.0060087*(체중)

우리는 이 방정식을 사용하여 무게를 고려하여 자동차의 예상 mpg를 찾을 수 있습니다. 예를 들어, 무게가 4,000파운드인 자동차의 mpg는 15,405여야 합니다.

예상 mpg = 39.44028 – 0.0060087*(4000) = 15.405

5단계: 결과를 보고합니다.

마지막으로 단순 선형 회귀의 결과를 보고하려고 합니다. 이를 수행하는 방법의 예는 다음과 같습니다.

자동차 중량과 갤런당 마일 간의 관계를 정량화하기 위해 선형 회귀가 수행되었습니다. 분석에는 74대의 자동차 샘플이 사용되었습니다.

결과는 체중과 mpg 사이에 통계적으로 유의미한 관계가 있으며(t = -11.60, p < 0.0001) 체중이 mpg의 설명된 변동성의 65.15%를 설명한다는 것을 보여주었습니다.

회귀 방정식은 다음과 같습니다.

예상 mpg = 39.44 – 0.006(체중)

파운드가 추가될 때마다 평균적으로 갤런당 -0.006마일이 감소했습니다.