대칭 분포

에 의해 벤자민 앤더슨 8월 5, 2023 통계 댓글 0개

이 기사에서는 대칭 분포가 무엇인지, 대칭 분포의 예, 분포가 대칭인지 비대칭인지 확인하는 방법을 배웁니다.

대칭 분포란 무엇입니까?

통계에서 대칭 분포는 평균 왼쪽과 평균 오른쪽에 동일한 수의 값이 있는 분포입니다. 즉, 대칭 분포에서 평균은 대칭 축입니다.

예를 들어, 정규 분포는 대칭 분포입니다.

모든 대칭 분포에서 평균은 중앙값과 같습니다. 그러나 분포가 단봉인 경우(통계 모드가 단일 값인 경우) 평균, 중앙값 및 모드는 동일합니다.

논리적으로 대칭 분포가 무엇인지 완전히 이해하려면 평균, 중앙값, 최빈값이 무엇인지 명확하게 알아야 합니다. 여기에서 이러한 통계 개념의 의미를 검토할 수 있습니다.

➤ 참고: 평균, 중앙값 및 최빈값이란 무엇입니까?

대칭 분포의 예

대칭 분포의 정의를 고려하면 이러한 분포 유형의 예가 아래에 나와 있습니다.

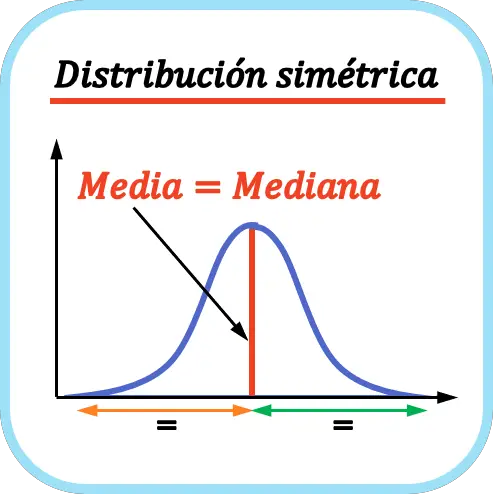
그래프에서 볼 수 있듯이 평균이 모든 데이터의 중앙에 있기 때문에 분포는 대칭입니다. 즉, 곡선 왼쪽의 꼬리가 오른쪽의 꼬리와 같습니다. 이 경우 모드가 단봉이므로 평균, 중앙값 및 모드가 동일합니다.

두 가지 다른 유형의 대칭 확률 분포의 두 가지 명확한 예는 정규 분포와 균일 분포입니다. 왜냐하면 평균의 왼쪽과 오른쪽에 동일한 수의 값이 있기 때문입니다.

반면에 분포는 대칭형 및 이봉형, 즉 두 가지 모드를 가질 수도 있습니다. 다음 예를 살펴보십시오.

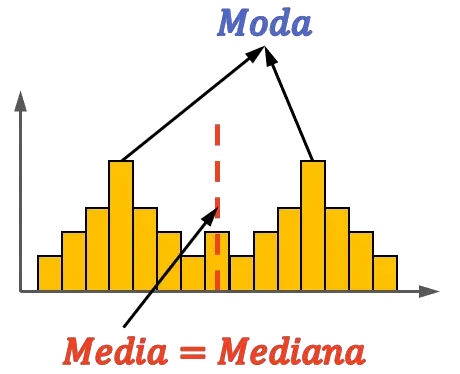
이 다른 예에서 볼 수 있듯이 이봉 분포는 다른 값에 관계없이 중앙에 평균과 중앙값을 가질 수 있기 때문에 대칭일 수도 있습니다. 그러나 이 경우 모드가 반드시 평균 및 모드와 같을 필요는 없습니다.

대칭성에 따른 다른 유형의 분포

대칭 분포 외에도 두 가지 다른 유형의 비대칭 분포가 있습니다.

대칭 분포 : 평균을 기준으로 왼쪽과 오른쪽에 동일한 수의 값이 있는 분포입니다.
양으로 치우친 분포 : 분포는 평균의 왼쪽보다 오른쪽에 더 많은 값이 있습니다.
음으로 치우친 분포 : 분포는 평균의 오른쪽보다 왼쪽에 더 많은 값이 있습니다.

분포가 대칭인지 확인하는 방법

분포가 대칭인지 아닌지를 결정하려면 Pearson 비대칭 계수를 계산해야 하며 그 공식은 다음과 같습니다.

$A_p=\cfrac{\mu-Mo}{\sigma}$

금

$A_p$

피어슨 계수이고,

$\mu$

산술 평균,

$Mo$

모드(통계) 및

$\sigma$

표준편차.

따라서 Pearson 비대칭 계수의 부호에 따라 분포는 대칭 또는 비대칭이 됩니다.

Pearson 왜도 계수가 양수이면 분포가 양수로 치우쳐 있다는 의미입니다.
피어슨 왜도 계수가 음수이면 분포가 음수로 치우쳐 있다는 의미입니다.
피어슨 왜도 계수가 0이면 분포가 대칭임을 의미합니다.

그러나 Pearson 계수는 분포가 단봉인 경우에만 계산할 수 있으며, 그렇지 않은 경우 공식은 다음과 같은 Fisher 비대칭 계수를 사용해야 합니다.

$\displaystyle\gamma_1=\frac{\displaystyle \sum_{i=1}^N\left(x_i-\mu\right)^3}{N\cdot \sigma ^3}$

금

$\mu$

산술 평균,

$\sigma$

표준편차

$N$

총 데이터 수입니다.

Fisher 비대칭 계수의 해석은 Pearson 계수와 동일합니다. 양수이면 분포가 양의 비대칭임을 의미하고 음수이면 분포가 음의 비대칭임을 의미하며 0이면 분포가 대칭임을 의미합니다.

저자 소개

벤자민 앤더슨

안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기