로그 우도 값을 해석하는 방법(예제 포함)

회귀 모델의 로그 우도 값은 모델의 적합도를 측정하는 방법입니다. 로그 우도 값이 높을수록 모델이 데이터 세트에 더 잘 맞는 것입니다.

주어진 모델에 대한 로그 우도 값의 범위는 음의 무한대에서 양의 무한대까지일 수 있습니다. 주어진 모델에 대한 실제 로그 우도 값은 일반적으로 의미가 없지만 둘 이상의 모델을 비교하는 데 유용합니다 .

실제로는 여러 회귀 모델을 데이터 세트에 맞추고 로그 우도 값이 가장 높은 모델을 데이터에 가장 잘 맞는 모델로 선택하는 경우가 많습니다.

다음 예는 실제로 다양한 회귀 모델에 대한 로그 우도 값을 해석하는 방법을 보여줍니다.

예: 로그 우도 값 해석

특정 동네에 있는 20개 주택의 침실 수, 욕실 수 및 판매 가격을 보여주는 다음 데이터 세트가 있다고 가정해 보겠습니다.

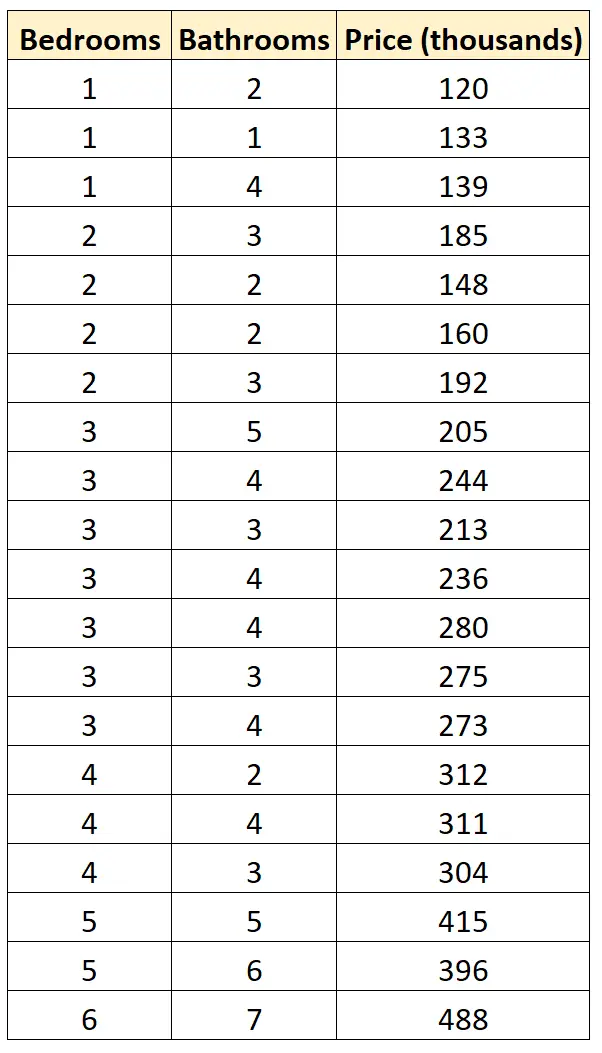
다음 두 가지 회귀 모델을 적합시키고 데이터에 가장 적합한 회귀 모델을 결정한다고 가정합니다.

모델 1 : 가격 = β ₀ + β ₁ (객실수)

모형 2 : 가격 = β ₀ + β ₁ (화장실 수)

다음 코드는 R에서 각 회귀 모델을 피팅하고 각 모델의 로그 우도 값을 계산하는 방법을 보여줍니다.

 #define data
df <- data. frame (beds=c(1, 1, 1, 2, 2, 2, 2, 3, 3, 3,
                        3, 3, 3, 3, 4, 4, 4, 5, 5, 6),
                 baths=c(2, 1, 4, 3, 2, 2, 3, 5, 4, 3,
                         4, 4, 3, 4, 2, 4, 3, 5, 6, 7),
                 price=c(120, 133, 139, 185, 148, 160, 192, 205, 244, 213,
                         236, 280, 275, 273, 312, 311, 304, 415, 396, 488))

#fitmodels
model1 <- lm(price~beds, data=df)
model2 <- lm(price~baths, data=df)

#calculate log-likelihood value of each model
logLik(model1)

'log Lik.' -91.04219 (df=3)

logLik(model2)

'log Lik.' -111.7511 (df=3)

첫 번째 모델은 두 번째 모델( -111.75 )보다 로그 우도 값( -91.04 )이 더 높습니다. 이는 첫 번째 모델이 데이터에 더 잘 맞는다는 의미입니다.

로그 우도 값 사용 시 주의 사항

로그 우도 값을 계산할 때 모델에 추가 예측 변수를 추가하면 추가 예측 변수가 통계적으로 유의하지 않더라도 거의 항상 로그 우도 값이 증가한다는 점에 유의하는 것이 중요합니다.

이는 각 모델에 동일한 수의 예측 변수가 있는 경우 두 회귀 모델 간의 로그 우도 값만 비교해야 함을 의미합니다.

예측 변수 수가 다른 모델을 비교하려면 우도 비 테스트를 수행하여 두 개의 중첩 회귀 모델의 적합도를 비교할 수 있습니다.

추가 리소스

R에서 선형 모델을 맞추기 위해 lm() 함수를 사용하는 방법
R에서 우도비 테스트를 수행하는 방법