머신러닝에서 과적합이란 무엇인가요? (설명 및 예시)

기계 학습에서는 특정 현상에 대해 정확한 예측을 할 수 있도록 모델을 구축하는 경우가 많습니다.

예를 들어, 고등학생에 대한 반응 변수의 ACT 점수를 예측하기 위해 학습에 소요된 예측 변수 시간 을 사용하는 회귀 모델을 생성한다고 가정합니다.

이 모델을 구축하기 위해 우리는 특정 학군의 수백 명의 학생을 대상으로 공부한 시간과 해당 ACT 점수에 대한 데이터를 수집합니다.

그런 다음 이 데이터를 사용하여 특정 학생이 공부한 총 시간을 기반으로 받을 점수를 예측할 수 있는 모델을 교육합니다 .

모델의 유용성을 평가하기 위해 모델의 예측이 관찰된 데이터와 얼마나 잘 일치하는지 측정할 수 있습니다. 이를 수행하기 위해 가장 일반적으로 사용되는 측정항목 중 하나는 다음과 같이 계산되는 평균 제곱 오차(MSE)입니다.

MSE = (1/n)*Σ(y _i – f( _xi )) ²

금:

• n: 총 관측치 수
• y _i : ^i번째 관측값의 응답 값
• f(x _i ): i ^번째 관측치의 예측 반응 값

모델 예측이 관측값에 가까울수록 MSE는 낮아집니다.

그러나 기계 학습에서 저지르는 가장 큰 실수 중 하나는 훈련 MSE를 줄이기 위해 모델을 최적화하는 것입니다. 즉, 모델 예측이 모델 훈련에 사용한 데이터와 얼마나 잘 일치하는지입니다.

모델이 훈련 MSE를 줄이는 데 너무 집중하면 훈련 데이터에서 단순히 우연히 발생한 패턴을 찾기가 너무 어려워지는 경우가 많습니다. 그러다가 보이지 않는 데이터에 모델을 적용하면 성능이 저하됩니다.

이 현상을 과적합 이라고 합니다. 이는 모델을 훈련 데이터에 너무 가깝게 “맞춤”하여 결국 새 데이터에 대한 예측에 유용하지 않은 모델을 구축할 때 발생합니다.

과적합의 예

과적합을 이해하기 위해 학습에 소요된 시간을 사용하여 ACT 점수를 예측하는 회귀 모델을 만드는 예로 돌아가 보겠습니다.

특정 학군의 학생 100명에 대한 데이터를 수집하고 두 변수 간의 관계를 시각화하기 위한 빠른 산점도를 생성한다고 가정해 보겠습니다.

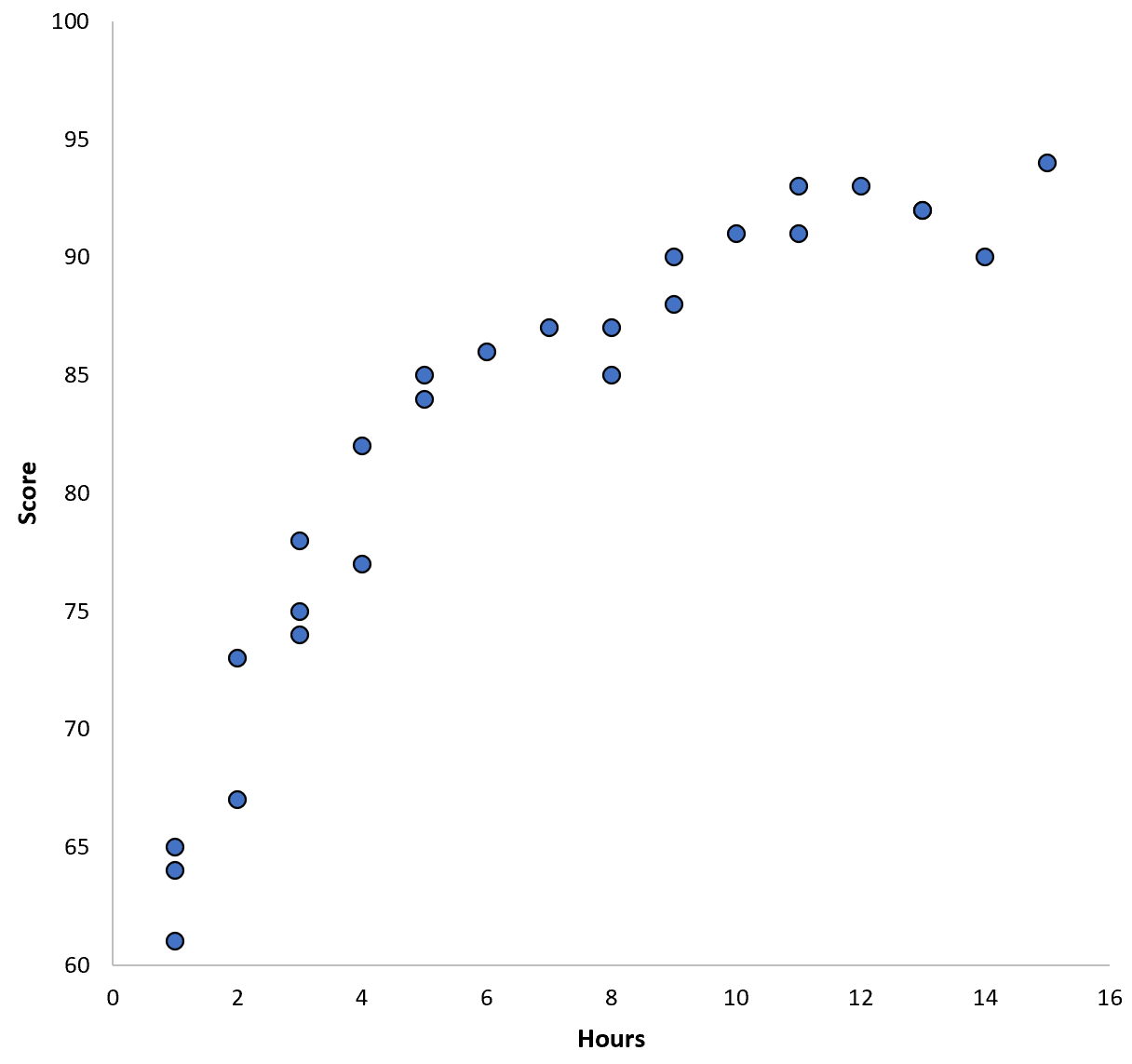
두 변수 사이의 관계는 2차 관계로 나타나므로 다음 2차 회귀 모델을 적용한다고 가정합니다.

점수 = 60.1 + 5.4*(시간) – 0.2*(시간) ²

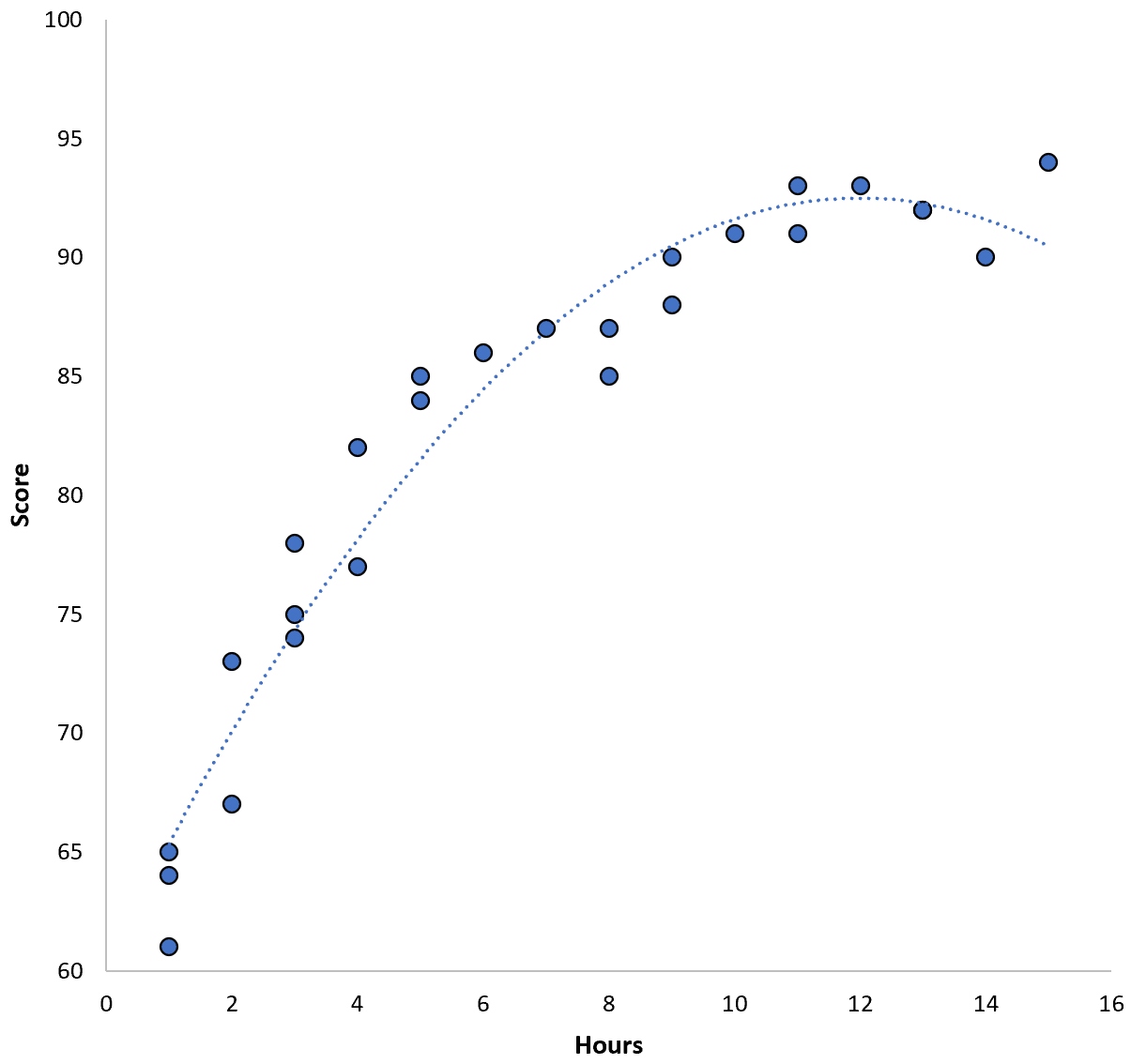
이 모델의 훈련 평균 제곱 오차(MSE)는 3.45 입니다. 즉, 모델에 의해 수행된 예측과 실제 ACT 점수 간의 평균 제곱근 차이는 3.45입니다.

그러나 우리는 고차 다항식 모델을 피팅하여 이 교육 MSE를 줄일 수 있습니다. 예를 들어 다음 모델을 적용한다고 가정해 보겠습니다.

점수 = 64.3 – 7.1*(시간) + 8.1*(시간) ² – 2.1*(시간) ³ + 0.2*(시간 ^{) 4 – 0.1*(시간) 5 +} 0.2(시간) ⁶

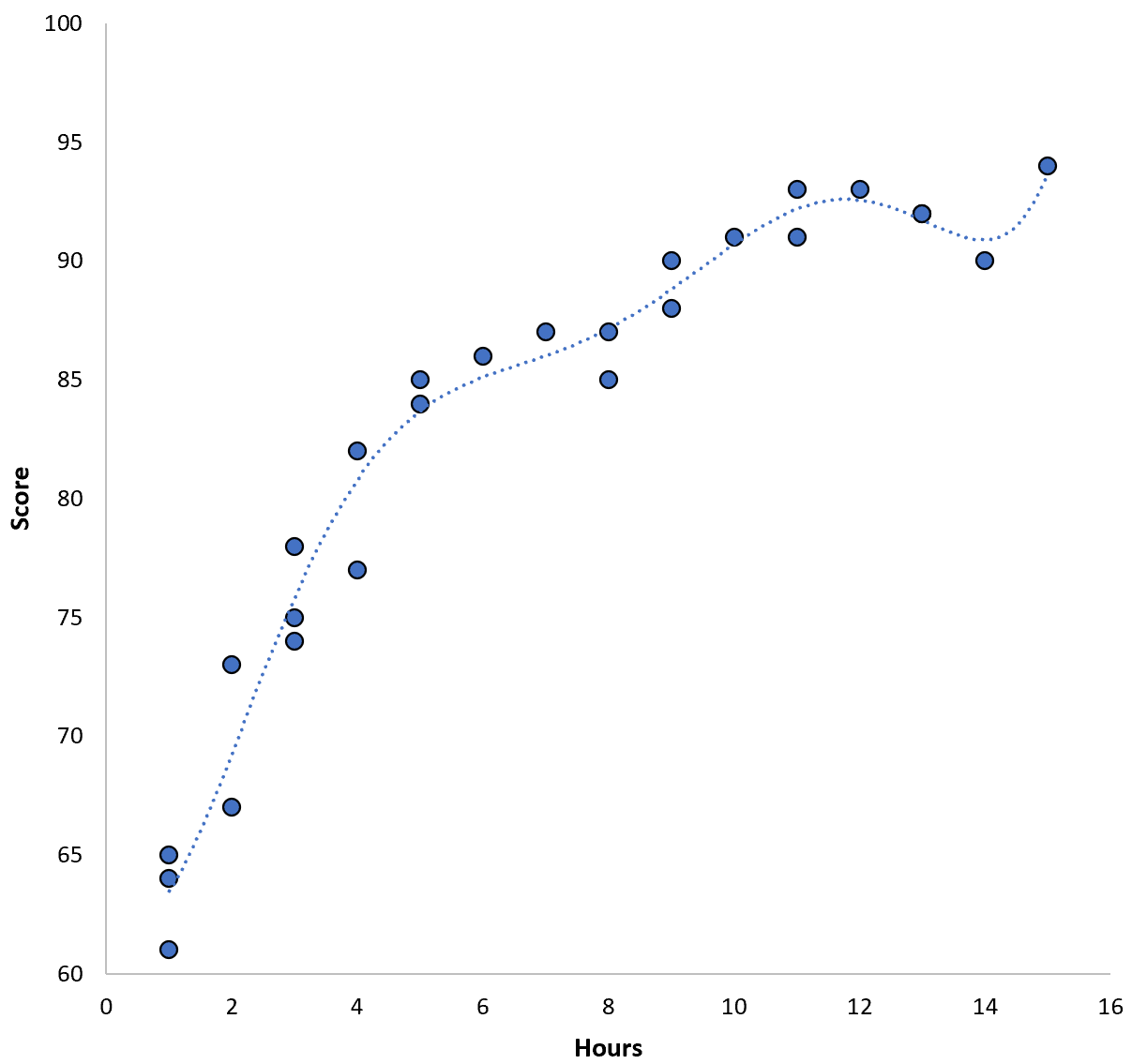
회귀선이 이전 회귀선보다 실제 데이터에 얼마나 더 가깝게 맞는지 확인하세요.

이 모델의 학습 평균 제곱근 오차(MSE)는 0.89 에 불과합니다. 즉, 모델에 의한 예측과 실제 ACT 점수 간의 평균 제곱근 차이는 0.89입니다.

이 MSE 훈련은 이전 모델에서 생성된 것보다 훨씬 작습니다.

그러나 우리는 훈련 MSE , 즉 모델의 예측이 모델 훈련에 사용한 데이터와 얼마나 잘 일치하는지에 대해서는 별로 신경 쓰지 않습니다. 대신 우리는 주로 MSE 테스트 , 즉 모델이 보이지 않는 데이터에 적용될 때의 MSE에 관심을 갖습니다.

위의 고차 다항식 회귀 모델을 보이지 않는 데이터 세트에 적용하면 단순한 2차 회귀 모델보다 성능이 저하될 가능성이 높습니다. 즉, 우리가 원하지 않는 더 높은 MSE 테스트가 생성됩니다.

과적합을 감지하고 방지하는 방법

과적합을 탐지하는 가장 간단한 방법은 교차 검증을 수행하는 것입니다. 가장 일반적으로 사용되는 방법은 k-겹 교차 검증 으로 알려져 있으며 다음과 같이 작동합니다.

1단계: 데이터 세트를 대략 동일한 크기의 k개 그룹, 즉 “접기”로 무작위로 나눕니다.

2단계: 접힌 부분 중 하나를 고정 세트로 선택합니다. 템플릿을 나머지 k-1 접기로 조정합니다. 인장된 플라이의 관찰에 대한 MSE 테스트를 계산합니다.

3단계: 매번 다른 세트를 제외 세트로 사용하여 이 프로세스를 k 번 반복합니다.

4단계: 테스트의 k MSE 평균으로 테스트의 전체 MSE를 계산합니다.

검정 MSE = (1/k)*ΣMSE _i

금:

• k: 접힌 횟수
• MSE _i : ^i번째 반복에서 MSE를 테스트합니다.

이 MSE 테스트는 주어진 모델이 알려지지 않은 데이터에서 어떻게 작동하는지에 대한 좋은 아이디어를 제공합니다.

실제로는 여러 가지 모델을 적합하고 각 모델에 대해 k-fold 교차 검증을 수행하여 MSE 테스트를 찾을 수 있습니다. 그런 다음 MSE 테스트가 가장 낮은 모델을 향후 예측에 사용할 최상의 모델로 선택할 수 있습니다.

이를 통해 단순히 훈련 MSE를 최소화하고 과거 데이터에 잘 “적합”하는 모델이 아니라 미래 데이터에서 가장 잘 수행될 가능성이 있는 모델을 선택할 수 있습니다.

추가 리소스

머신러닝의 편향-분산 트레이드오프는 무엇인가요?
K-폴드 교차 검증 소개
기계 학습의 회귀 및 분류 모델