포아송 분포 소개

포아송 분포는 통계학에서 가장 널리 사용되는 분포 중 하나입니다.

포아송 분포를 이해하려면 먼저 포아송 실험을 이해하는 것이 도움이 됩니다.

물고기 실험

포아송 실험은 다음과 같은 특성을 갖는 실험입니다.

• 실험의 성공 횟수를 셀 수 있습니다.
• 특정 시간(또는 공간) 간격 동안 발생한 평균 성공 횟수가 알려져 있습니다.
• 각 결과는 독립적입니다.
• 성공 확률은 간격의 크기에 비례합니다.

포아송 실험의 예로는 특정 병원의 시간당 출생 수를 들 수 있습니다. 예를 들어, 특정 병원에서 시간당 평균 10건의 출산이 이루어진다고 가정해 보겠습니다. 이는 다음과 같은 네 가지 특성을 갖기 때문에 포아송 실험입니다.

• 실험의 성공 횟수를 셀 수 있습니다 – 출생 횟수를 셀 수 있습니다.
• 특정 시간 간격 동안 발생하는 평균 출생 수는 알려져 있습니다. 시간당 평균 10명의 출생이 있는 것으로 알려져 있습니다.
• 각 결과는 독립적입니다. 한 엄마가 주어진 시간에 출산할 확률은 다른 엄마가 출산할 확률과 독립적입니다.
• 성공 확률은 간격의 크기에 비례합니다. 시간 간격이 길수록 출산 확률이 높아집니다.

포아송 분포를 사용하여 다음과 같은 포아송 실험의 확률에 대한 질문에 대답할 수 있습니다.

• 주어진 시간에 12명 이상의 출산이 일어날 확률은 얼마입니까?
• 주어진 시간에 5명 미만의 출생이 발생할 확률은 얼마입니까?
• 주어진 시간에 8~11명의 아이가 태어날 확률은 얼마입니까?

물고기 분포

포아송 분포는 주어진 시간 간격 동안 k개의 성공을 얻을 확률을 설명합니다.

확률 변수 X가 포아송 분포를 따르는 경우 X = k 성공 확률은 다음 공식으로 찾을 수 있습니다.

P(X=k) = λ ^k * e ^{– λ} / k!

금:

• λ: 특정 간격 동안 발생하는 평균 성공 횟수
• k: 성공 횟수
• e: 대략 2.71828과 같은 상수

예를 들어, 특정 병원에서 시간당 평균 2건의 출산이 발생한다고 가정해 보겠습니다. 위의 공식을 사용하여 0, 1, 2, 3번의 출산 등을 경험할 확률을 결정할 수 있습니다. 주어진 시간에:

P(X=0) = 2 ⁰ * e ^{– 2} / 0! = 0.1353

P(X=1) = 2 ¹ * e ^{– 2} / 1! = 0.2707

P(X=2) = 2 ² * e ^{– 2} / 2! = 0.2707

P(X=3) = 2 ³ * e ^{– 2} / 3! = 0.1805

우리는 무한대까지 출생의 확률을 계산할 수 있습니다. 그런 다음 이 확률 분포를 시각화하기 위해 간단한 히스토그램을 만듭니다.

누적 포아송 확률 계산

위의 공식을 사용하여 단일 포아송 확률(예: 병원이 주어진 시간에 3명의 출산을 경험할 확률)을 계산하는 것은 간단하지만 누적 포아송 확률을 계산하려면 개별 확률을 추가해야 합니다.

예를 들어, 병원에서 주어진 시간에 1회 이하의 출산이 발생할 확률을 알고 싶다고 가정해 보겠습니다. 이 확률을 계산하기 위해 다음 공식을 사용합니다.

P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406

이는 여러 확률을 추가하는 것과 관련되므로 누적 확률 이라고 합니다. 비슷한 공식을 사용하여 주어진 시간에 k 개 이하의 출산이 발생할 누적 확률을 계산할 수 있습니다.

P(X≤0) = P(X=0) = 0.1353

P(X≤1) = P(X=0) + P(X=1) = 0.1353 + 0.2707 = 0.406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0.1353 + 0.2707 + 0.2707 = 0.6767

우리는 무한대까지의 출생 수에 대해 이러한 누적 확률을 계산할 수 있습니다. 그런 다음 이 누적 확률 분포를 시각화하기 위해 히스토그램을 만들 수 있습니다.

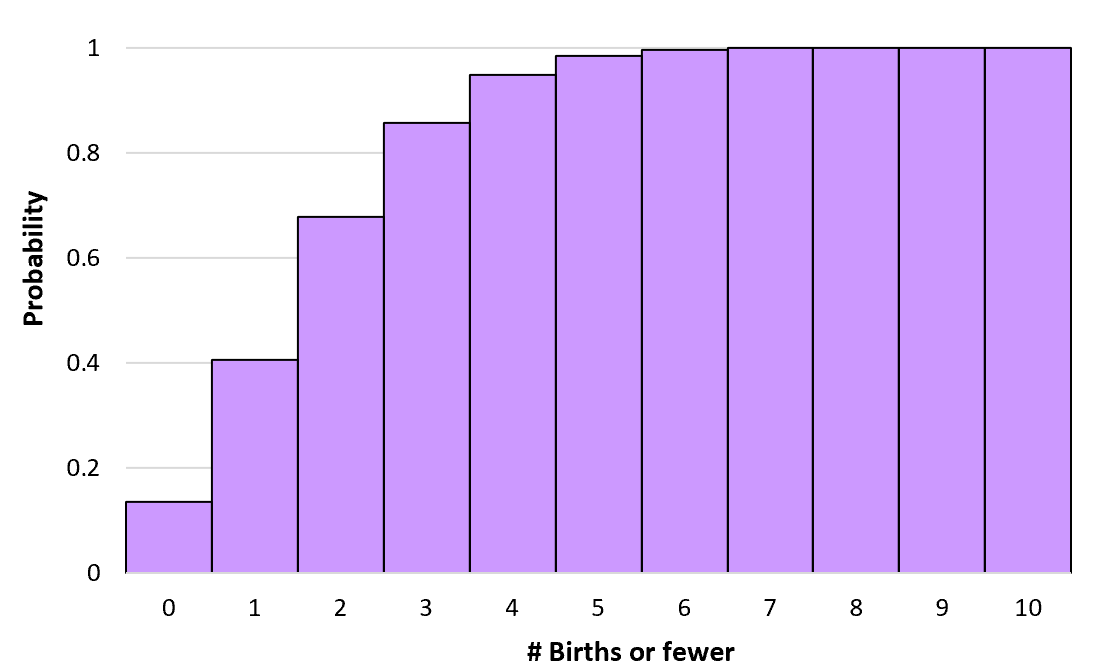
포아송 분포의 속성

포아송 분포에는 다음과 같은 속성이 있습니다.

분포의 평균은 λ 입니다.

분포의 분산 도 입니다.

분포의 표준편차는 √ λ 입니다.

예를 들어, 병원에서 시간당 평균 2건의 출산이 이루어진다고 가정해 보겠습니다.

특정 시간에 예상되는 평균 출생 수는 λ = 2 출생입니다.

우리가 기대하는 출생 수의 분산은 λ = 2 출생입니다.

생선 유통 실무 문제

다음 연습 문제를 사용하여 포아송 분포에 대한 지식을 테스트하세요.

참고: 이러한 질문에 대한 답을 계산하기 위해 포아송 분포 계산기를 사용할 것입니다.

문제 1

질문: 특정 웹사이트에서 시간당 10개의 매출이 발생한다는 것을 알고 있습니다. 주어진 시간에 사이트에서 정확히 8개의 매출을 올릴 확률은 얼마입니까?

답: λ = 10 및 x = 8인 포아송 분포 계산기를 사용하면 P(X=8) = 0.1126 이라는 것을 알 수 있습니다.

문제 2

질문: 어떤 부동산 중개업자는 한 달에 평균 5건의 매출을 올리는 것으로 알고 있습니다. 특정 달에 그녀가 7개 이상의 판매를 할 확률은 얼마입니까?

답변: λ = 5 및 x = 7인 포아송 분포 계산기를 사용하면 P(X>7) = 0.13337 이라는 것을 알 수 있습니다.

문제 3

질문: 우리는 특정 병원에서 시간당 4건의 배달이 발생한다는 것을 알고 있습니다. 주어진 시간에 4명 이하의 출생이 발생할 확률은 얼마입니까?

답변: λ = 4 및 x = 4인 포아송 분포 계산기를 사용하면 P(X≤4) = 0.62884 라는 것을 알 수 있습니다.

추가 리소스

다음 기사에서는 다양한 통계 소프트웨어에서 포아송 분포를 사용하는 방법을 설명합니다.

R에서 포아송 분포를 사용하는 방법
Excel에서 포아송 분포를 사용하는 방법
TI-84 계산기에서 포아송 확률을 계산하는 방법
포아송 분포의 실제 사례
생선 분포 계산기