베타 배포

에 의해 벤자민 앤더슨 8월 4, 2023 개연성 댓글 0개

이 문서에서는 베타 배포가 무엇인지, 그리고 어떤 용도로 사용되는지 설명합니다. 마찬가지로 베타 분포 그래프와 이러한 유형의 확률 분포의 속성을 볼 수 있습니다.

베타 배포란 무엇입니까?

베타 분포는 구간 (0,1)에서 정의되고 두 개의 양수 매개변수인 α와 β로 매개변수화되는 확률 분포입니다. 즉, 베타 분포의 값은 매개변수 α와 β에 따라 달라집니다.

따라서 베타 분포의 주요 특징은 그 모양이 매개변수 α와 β에 의해 제어될 수 있다는 것입니다. 또한 베타 분포는 값이 0과 1 사이인 확률 변수를 정의하는 데 사용됩니다.

연속 확률 변수가 베타 분포의 영향을 받는다는 것을 나타내는 몇 가지 표기법이 있으며, 가장 일반적인 표기법은 다음과 같습니다.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex]X\sim Beta(\alpha,\beta)\\[2ex]X\sim \beta_{\alpha,\beta}\end{array}$

통계에서 베타 배포판은 매우 다양한 용도로 사용됩니다. 예를 들어, 베타 분포는 다양한 표본의 백분율 변화를 연구하는 데 사용됩니다. 마찬가지로 프로젝트 관리에서는 베타 배포를 사용하여 Pert 분석을 수행합니다.

베타 분포도

베타분포의 정의를 고려하여 베타분포의 밀도함수와 확률분포함수를 아래에 그려본다.

아래에서는 베타 분포의 밀도 함수 그래프가 매개변수 α 및 β에 따라 어떻게 달라지는지 확인할 수 있습니다.

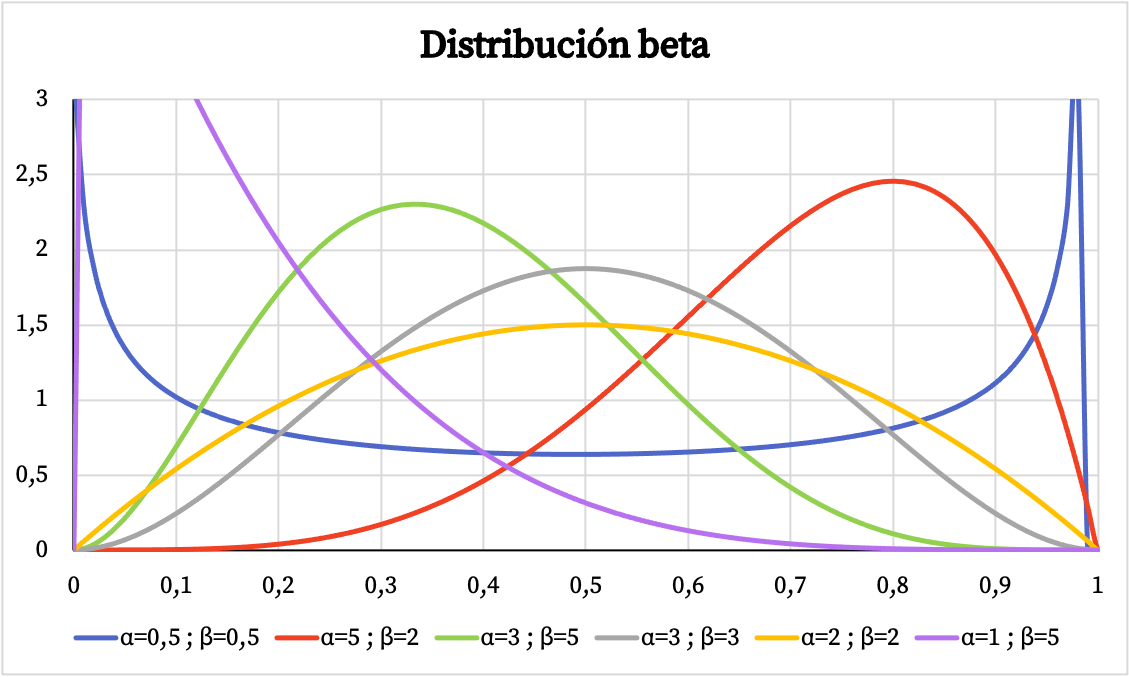
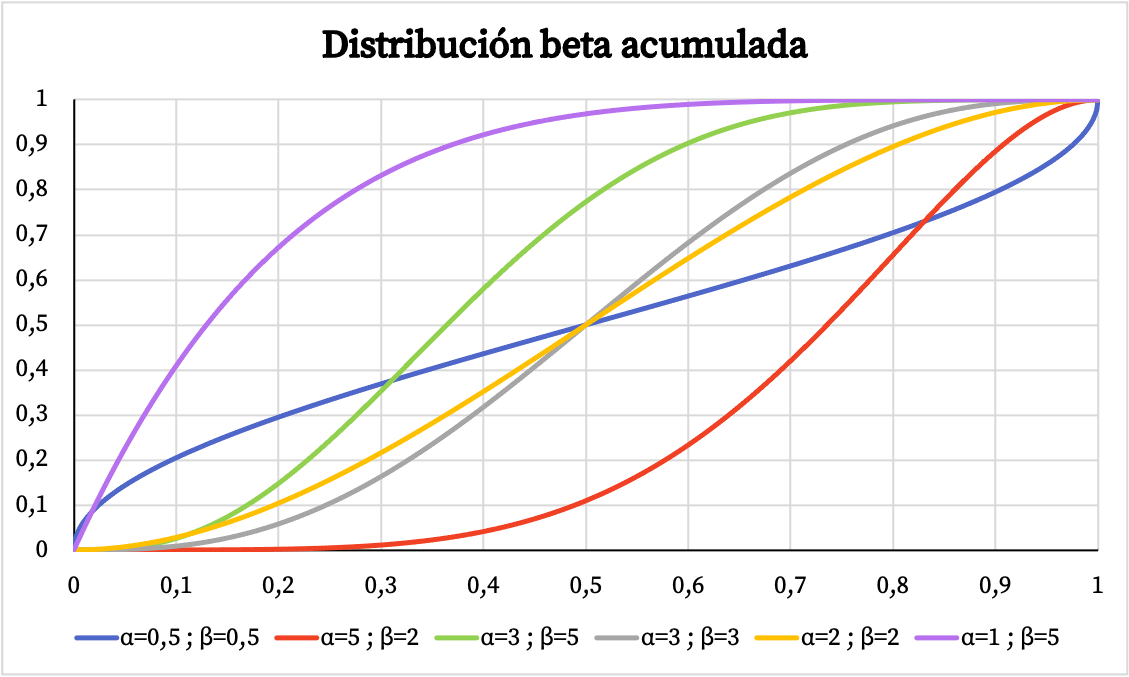
마찬가지로 아래에서는 매개변수 α 및 β를 기반으로 베타 분포의 누적 확률을 그래픽으로 표현한 것을 볼 수 있습니다.

베타 분포의 특징

이 섹션에서는 베타 배포의 가장 중요한 특성이 무엇인지 살펴보겠습니다.

베타 분포의 매개변수 α와 β는 실수와 양수입니다.

$\begin{array}{c}\alpha >0\\[2ex] \beta >0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”44″ style=”vertical-align: 0px;”></p> </p> <ul> <li> 베타 분포의 영역 범위는 0에서 1까지이며 두 극단은 포함되지 않습니다.</li> </ul> <p class=$ $x\in (0,1)$

베타 분포의 평균은 알파를 알파 더하기 베타의 합으로 나눈 값과 같습니다.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] E[X]=\cfrac{\alpha}{\alpha+\beta}\end{array}$

베타 분포의 분산은 다음 공식을 사용하여 계산할 수 있습니다.

$\begin{array}{c}X\sim B(\alpha,\beta)\\[2ex] Var(X)=\cfrac{\alpha\cdot \beta}{(\alpha+\beta+1)\cdot (\alpha+\beta)^2}\end{array}$

1보다 큰 알파 및 베타 값의 경우 베타 분포 모드는 다음 표현식으로 쉽게 찾을 수 있습니다.

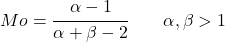
$Mo=\cfrac{\alpha-1}{\alpha+\beta-2}\qquad \alpha,\beta>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”225″ style=”vertical-align: -16px;”></p> </p> <ul> <li> 베타 분포의 밀도 함수는 다음과 같습니다.</li> </ul> <p class=$ $\displaystyle P[X=x]=\frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha,\beta)}$