Excel에서 사분위수 범위(iqr)를 계산하는 방법

이 튜토리얼에서는 Excel에서 데이터 세트의 사분위수 범위를 계산하는 방법을 설명합니다.

사분위수 범위란 무엇입니까?

IQR이라고도 불리는 사분위간 범위는 데이터 세트의 중간 50% 분포를 측정하는 방법입니다. 이는 데이터 세트의 첫 번째 사분위수*(Q1)와 세 번째 사분위수(Q3) 간의 차이로 계산됩니다.

*사분위수는 단순히 데이터 세트를 4개의 동일한 부분으로 나누는 값입니다.

예를 들어 다음과 같은 데이터 세트가 있다고 가정해 보겠습니다.

[58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98]

세 번째 사분위수는 91 이고 첫 번째 사분위수는 75.5 입니다. 따라서 이 데이터 세트의 사분위간 범위(IQR)는 91 – 75.5 = 15 입니다. 이는 이 데이터세트에 있는 값의 중간 50%의 분포를 알려줍니다.

Excel에서 사분위수 범위를 계산하는 방법

Microsoft Excel에는 데이터 세트의 IQR을 계산하는 내장 함수가 없지만 다음 인수를 사용하는 QUARTILE() 함수를 사용하여 쉽게 찾을 수 있습니다.

QUARTILE(배열, 쿼터)

• array: 관심 있는 데이터 배열입니다.
• quart: 계산하려는 사분위수입니다.

예: Excel에서 IQR 검색

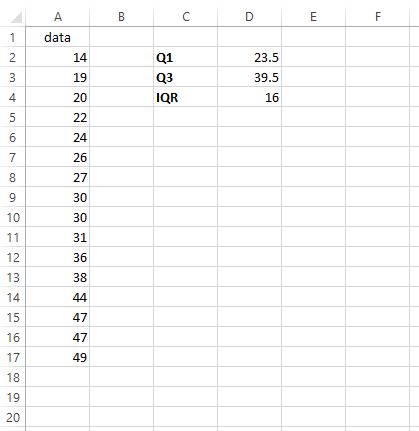
다음 데이터 세트에 대한 IQR을 찾고 싶다고 가정해 보겠습니다.

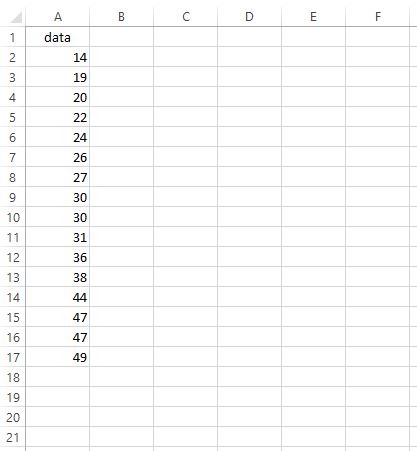
IQR을 찾으려면 다음 단계를 수행할 수 있습니다.

1단계: Q1을 검색합니다 .

첫 번째 사분위수를 찾으려면 원하는 셀에 =QUARTILE(A2:A17, 1)을 입력하면 됩니다.

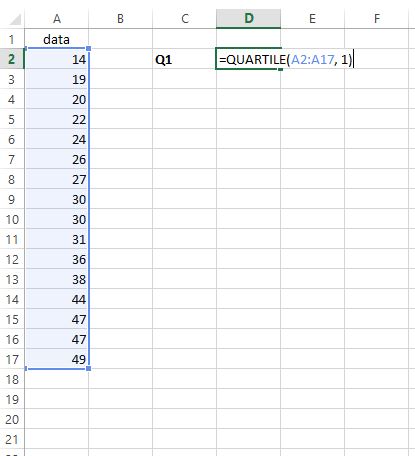
2단계: Q3을 검색합니다 .

세 번째 사분위수를 찾으려면 원하는 셀에 =QUARTILE(A2:A17, 3)을 입력합니다.

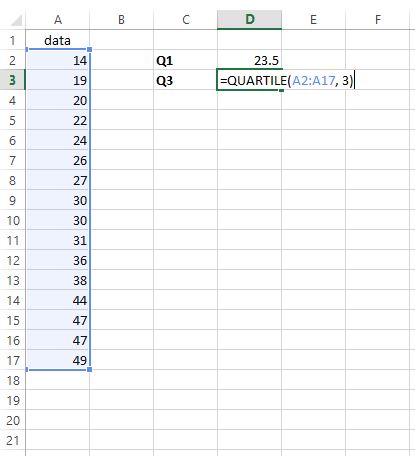
3단계: IQR을 찾습니다 .

사분위간 범위(IQR)를 찾으려면 Q3에서 Q1을 빼면 됩니다.

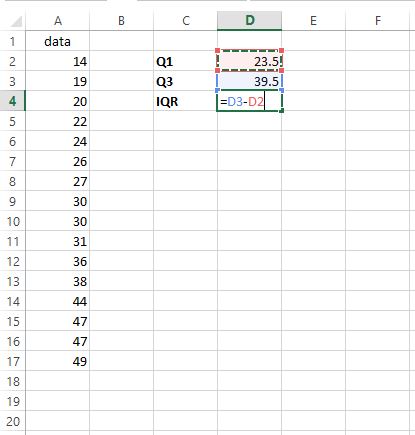
IQR은 39.5 – 23.5 = 16 입니다. 이는 이 특정 데이터 세트에서 값의 중간 50%가 얼마나 분포되어 있는지 알려줍니다.

더 짧은 접근 방식

이전 예에서는 다음 공식을 사용하여 데이터세트의 사분위수 범위를 찾을 수도 있었습니다.

=사분위수(A2:A17, 3) – 사분위수(A2:A17, 1)

이는 또한 값 16 을 제공합니다.

결론

사분위간 범위는 데이터 세트의 “확산”을 측정하는 한 가지 방법일 뿐입니다. 스프레드를 측정하는 다른 방법으로는 범위, 표준 편차 및 분산이 있습니다.

IQR을 사용하여 스프레드를 측정할 때의 장점은 이상값에 강하다는 것입니다. 이는 데이터 세트의 중간 50%의 분포만을 알려주기 때문에 비정상적으로 작거나 비정상적으로 큰 이상값의 영향을 받지 않습니다.

이는 단순히 데이터 세트에서 가장 큰 값과 가장 작은 값 사이의 차이를 알려주는 범위와 같은 측정항목에 비해 분산을 측정하는 데 더 바람직한 방법입니다.

관련 항목: Excel에서 중간 범위를 계산하는 방법