Iqr(사분위간 범위)이 특이치의 영향을 받나요?

통계에서 우리는 분포에서 값이 얼마나 광범위하게 “확산”되어 있는지 알고 싶어하는 경우가 많습니다.

확산을 측정하는 널리 사용되는 방법은 사분위간 범위 입니다. 이는 데이터 세트의 첫 번째 사분위수와 세 번째 사분위수 간의 차이로 계산됩니다. 사분위수는 단순히 데이터 세트를 4개의 동일한 부분으로 나누는 값입니다.

예: 사분위수 범위 계산

다음 예에서는 지정된 데이터 세트의 사분위간 범위를 계산하는 방법을 보여줍니다.

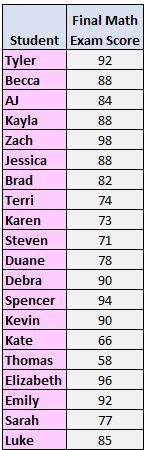
1단계: 가장 작은 것부터 가장 큰 것 순으로 값을 정렬합니다.

58, 66, 71, 73, 74, 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

2. 중앙값을 구합니다.

58, 66, 71, 73, 74, 77 , 78, 82 , 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

이 경우 중앙값은 85에서 88 사이입니다.

3. 중앙값은 데이터 세트를 두 부분으로 나눕니다. 하반부의 중앙값은 하사분위수이고 상반부의 중앙값은 상분위수입니다.

58, 66, 71, 73 , 74 , 77, 78, 82, 84, 85, 88, 88, 88, 90, 90, 92, 92, 94, 96, 98

4. 사분위수 범위를 계산합니다.

이 경우, 1분위수는 데이터세트의 하단(75.5)에 있는 가운데 2개 값의 평균이고, 3분위수는 세트 데이터의 상단에 있는 중간 2개 값의 평균이다. (91).

따라서 사분위간 범위는 91 – 75.5 = 15.5 입니다.

사분위수 범위는 특이치의 영향을 받지 않습니다.

사람들이 데이터 세트의 “확산”을 계산할 때 사분위수 범위(IQR)를 사용하는 것을 선호하는 이유 중 하나는 이상치에 강하다는 것입니다. IQR은 단순히 데이터 값의 중간 50% 범위이므로 극단적인 이상값 의 영향을 받지 않습니다.

이를 입증하려면 다음 데이터세트를 고려하세요.

[1, 4, 8, 11, 13, 17, 17, 20]

이 데이터세트에 대한 다양한 전파 측정항목은 다음과 같습니다.

• 사분위간 범위: 11
• 범위: 19
• 표준편차: 6.26
• 차이: 39.23

이제 동일한 데이터 세트에 극단적인 이상값이 추가된 경우를 생각해 보세요.

[1, 4, 8, 11, 13, 17, 17, 20, 150 ]

이 데이터세트에 대한 다양한 전파 측정항목은 다음과 같습니다.

• 사분위간 범위: 12.5
• 범위: 149
• 표준편차: 43.96
• 스프레드: 1,932.84

사분위간 범위가 11에서 12.5까지 약간만 변경되는 것을 확인하세요. 그러나 분산에 대한 다른 모든 측정값은 극적으로 변합니다.

이는 사분위수 범위가 다른 분산 측정값과 같은 이상치의 영향을 받지 않음을 보여줍니다. 이러한 이유로 모든 분포에서 중간 50% 값의 분포를 측정하는 신뢰할 수 있는 방법입니다.

추가 자료:

분산 측정
사분위간 범위 계산기