상자수염 도표

에 의해 벤자민 앤더슨 8월 5, 2023 통계 댓글 0개

이 문서에서는 상자 그림(또는 상자 그림)이라고도 알려진 상자 그림이 무엇인지 설명합니다. 이러한 유형의 통계 다이어그램이 어떻게 만들어지는지 알아보고 상자 수염 다이어그램의 연습 문제와 그 해석을 알아보세요.

상자수염도란 무엇입니까?

상자 그림 또는 상자 그림 이라고도 하는 상자 그림은 사분위수를 사용하여 일련의 통계 데이터를 시각적으로 나타내는 그래프입니다.

상자 수염 플롯의 주요 특징은 데이터의 사분위수, 중앙값, 극단값 및 이상값을 나타내기 때문에 일련의 데이터의 분산을 빠르게 시각화할 수 있다는 것입니다.

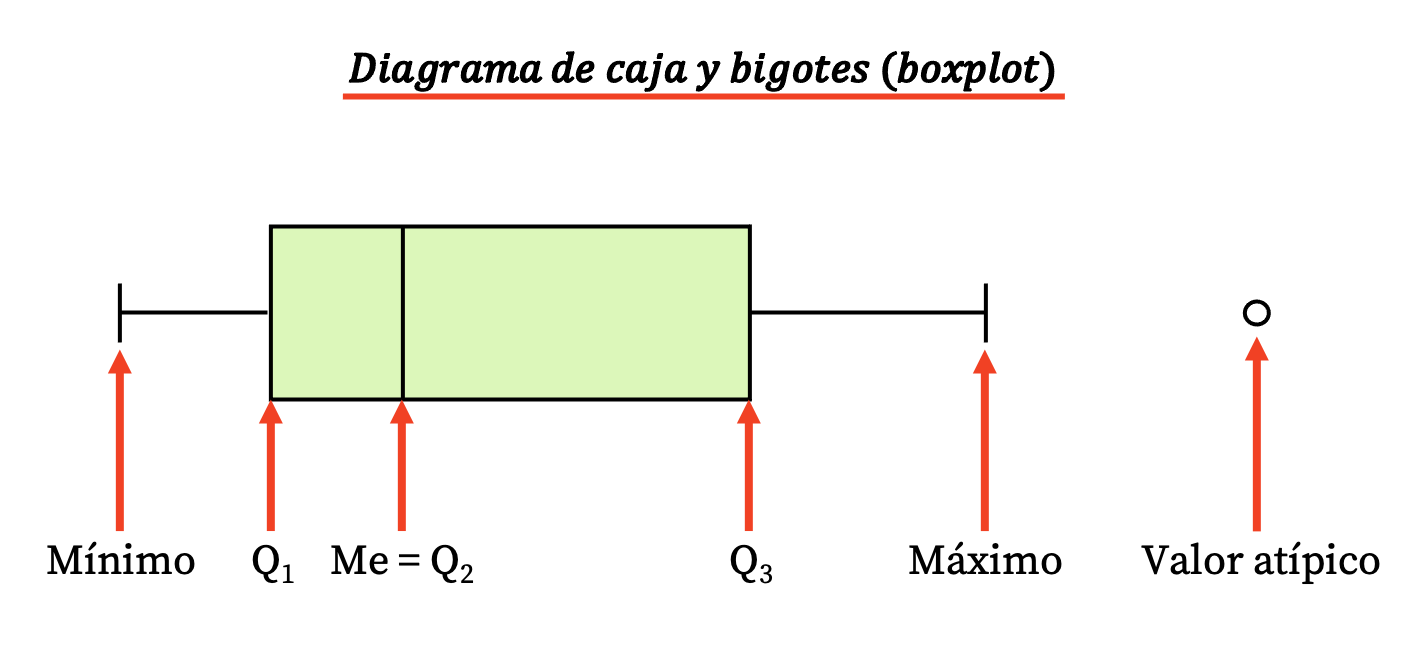
따라서 이러한 유형의 다이어그램은 직사각형 상자와 다음 값이 나타나는 몇 개의 선(또는 수염)으로 구성됩니다.

상자의 경계는 첫 번째 및 세 번째 사분위수 (Q ₁ 및 Q ₃ )를 나타냅니다. 그리고 상자 안의 수직선은 중앙값 (2사분위수 _Q2 에 해당)입니다.
수염(또는 팔)의 한계는 극값 , 즉 데이터 계열의 최소값과 최대값입니다.
수염 외부의 점은 이상치 입니다. 즉, 잘못 측정되었을 가능성이 있는 데이터 이므로 통계 연구에서 고려하면 안 됩니다.

상자 그림 또는 상자 그림

세 번째 사분위수와 첫 번째 사분위수 사이의 차이는 통계적 분산의 또 다른 척도인 사분위수 범위(또는 사분위수 범위)입니다.

상자 및 수염 도표는 수치 변수를 비교하는 데 매우 유용합니다. 그러나 범주형 변수를 표현하는 데는 적합하지 않습니다.

상자 수염 그림을 만드는 방법

데이터 계열에서 상자 수염 그림(또는 상자 그림)을 만들려면 다음 단계를 수행해야 합니다.

통계 데이터 예시를 정리해보세요.
사분위수(Q ₁ , Q ₂ 및 Q ₃ )를 계산하고 이를 다이어그램의 상자로 표시합니다. 첫 번째 및 세 번째 사분위수는 상자의 한계에 해당하며 중앙값(두 번째 사분위수)을 나타내려면 해당 값이 있는 상자 내부에 선을 그려야 합니다.
세 번째 사분위수에서 첫 번째 사분위수를 뺀 값과 동일한 사분위수 범위를 계산합니다.

$IQR=Q_3-Q_1$

허용 가능한 값 LI 및 LS를 계산합니다. 공식은 다음과 같습니다.

$LI=Q_1-1,5\cdot IQR$

$LS=Q_3+1,5\cdot IQR$

LI보다 작거나 LS보다 큰 값인 샘플 이상값을 식별합니다. 수염 범위 밖의 값을 점으로 표시합니다.
LI와 LS로 구성된 구간에서 가장 작은 값과 가장 큰 값인 극값을 식별하고 표현합니다. 이 값은 다이어그램에서 두 수염의 끝을 나타냅니다.

상자 수염 그림 예

상자 수염 도표(또는 상자 도표)의 정의와 이론을 고려하면 개념을 더 잘 이해하고 이러한 유형의 통계 도표가 어떻게 수행되는지 확인할 수 있는 구체적인 예가 아래에 나와 있습니다.

다음 통계 데이터 세트의 상자 그림을 그립니다.

이 경우 데이터는 이미 가장 작은 것부터 가장 큰 것 순으로 정렬되어 있으므로 변경할 필요가 없습니다. 그렇지 않으면 샘플 데이터를 먼저 정렬해야 합니다.

둘째, 표본의 사분위수를 추출합니다.

$Q_1=4,06$

$Q_2=4,38$

$Q_3=4,66$

➤ 참고: 사분위수 계산기

3분위수를 계산한 후에는 3분위수에서 1분위수를 빼서 사분위수 범위를 찾습니다.

$IQR=Q_3-Q_1=4,66-4,06=0,6$

이제 데이터가 비정형으로 간주되는 값인 LI 및 LS 한계를 계산합니다. 이렇게 하려면 다음 수식을 사용해야 합니다.

$LI=Q_1-1,5\cdot IQR=4,06-1,5\cdot 0,6=3,16$

$LS=Q_3+1,5\cdot IQR=4,66+1,5\cdot 0,6=5,56$

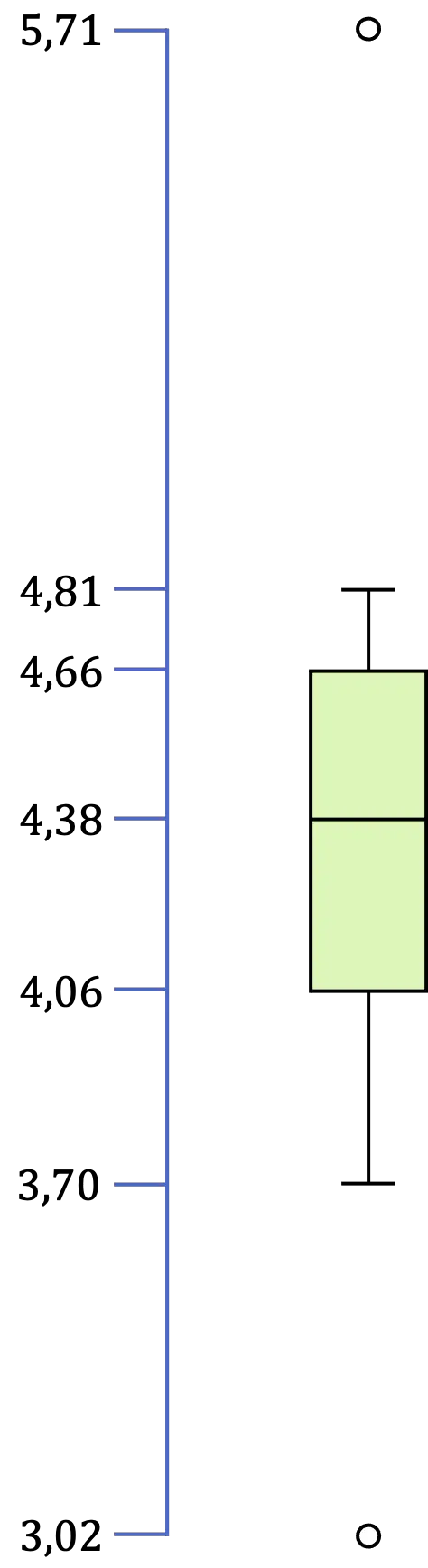
따라서 이 경우에는 3.02가 3.16보다 작고 5.71이 5.56보다 크기 때문에 두 개의 이상값이 있습니다.

$\text{Valores at\'ipicos} =\Bigl\{3,02 \ ; \ 5,71\Bigr\}$

마지막으로 [LI,LS] 구간에 있는 모든 데이터의 최소값과 최대값인 극값을 식별하는 작업이 남아 있습니다. 따라서 이 예에서는 최소값은 3.70이고 최대값은 4.81입니다.

$\text{M\'inimo}=3,70$

$\text{M\'aximo}=4,81$

따라서 상자와 수염 플롯의 모든 값을 식별한 후에 남은 것은 그래픽 표현을 만드는 것입니다.

상자 그림 예

상자수염도는 어떤 용도로 사용되나요?

마지막으로 상자 수염 플롯(또는 상자 플롯)이 무엇인지, 어떻게 해석하는지 살펴보겠습니다.

분명히 상자 및 수염 플롯은 데이터 계열의 사분위수, 사분위간 범위, 중앙값, 극단값 및 이상값을 빠르게 파악하는 데 매우 유용합니다. 이러한 모든 통계 측정값은 간단한 보기로 식별할 수 있기 때문입니다.

또한 상자 수염 플롯은 전체 데이터 세트를 시각적으로 나타내기 때문에 통계 샘플의 대칭성을 분석하는 데 사용됩니다. 중앙값이 상자 중앙에 있지 않으면 표본이 대칭이 아니라는 의미입니다.

마찬가지로, 상자 그림은 단기간에 최대값, 최소값 및 중간값을 볼 수 있기 때문에 주식 시장에서 일정 기간 동안의 주식 가격 변동을 나타내는 데 널리 사용됩니다. 시간을 들여 더 빠른 결정을 내릴 수 있습니다.

저자 소개

벤자민 앤더슨

안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기

의견을 추가하다