Ti-84 계산기에서 선형 회귀를 수행하는 방법

선형 회귀는 설명 변수 x와 응답 변수 y 사이의 관계를 이해하는 데 사용할 수 있는 방법입니다.

이 튜토리얼에서는 TI-84 계산기에서 선형 회귀를 수행하는 방법을 설명합니다.

예: TI-84 계산기의 선형 회귀

학생이 시험을 위해 공부한 시간과 시험에서 받는 성적 사이의 관계를 이해하고 싶다고 가정해 보겠습니다.

이 관계를 탐색하기 위해 TI-84 계산기에서 다음 단계를 수행하여 학습 시간을 설명 변수로, 시험 성적을 응답 변수로 사용하여 간단한 선형 회귀를 수행할 수 있습니다.

1단계: 데이터를 입력합니다.

먼저 설명변수와 반응변수에 대한 데이터 값을 입력하겠습니다. Stat를 누른 다음 EDIT를 누릅니다. L1 열에 설명 변수(학습 시간)에 다음 값을 입력하고 L2 열에 응답 변수(시험 점수)에 대한 값을 입력합니다.

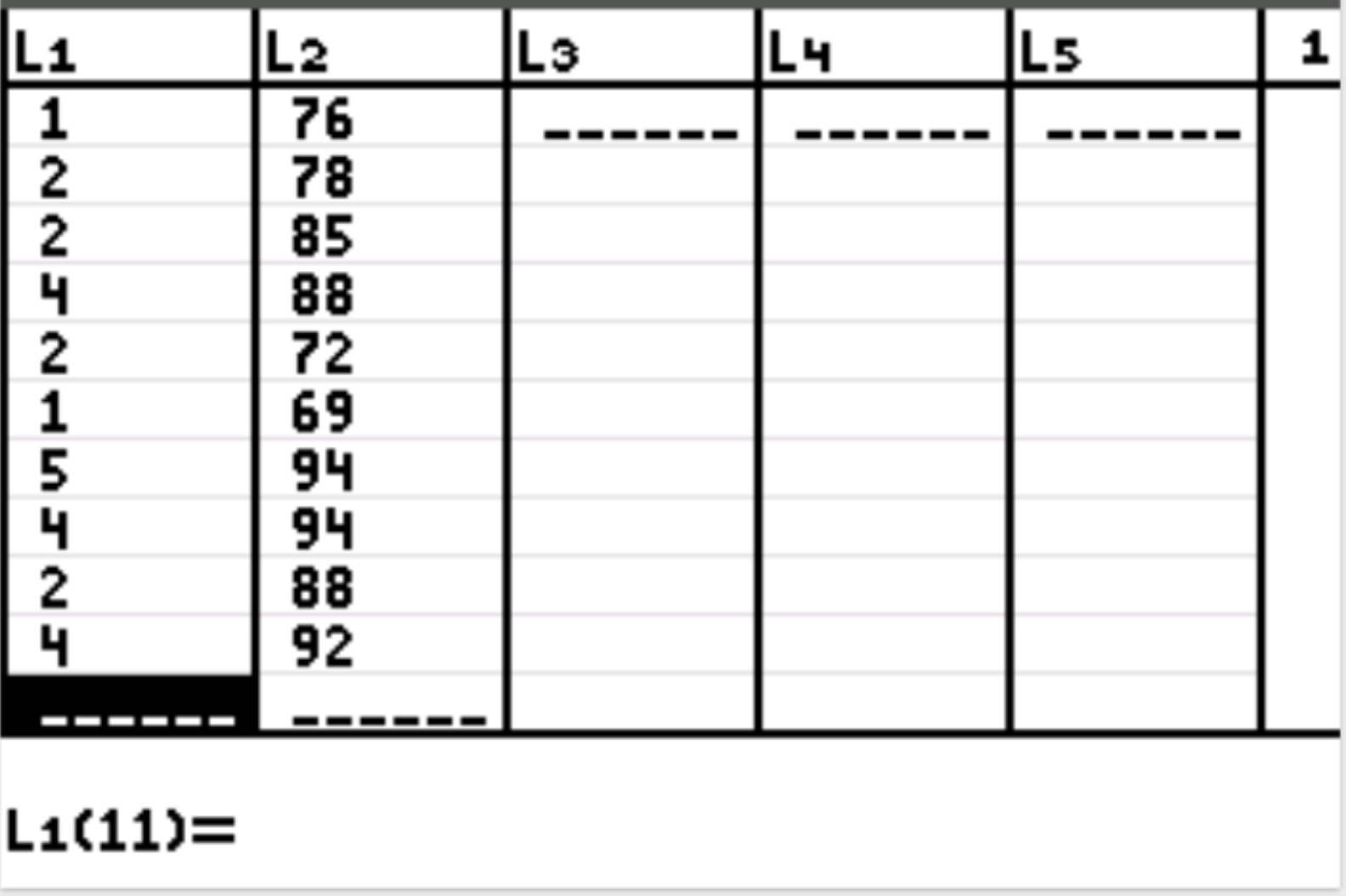
2단계: 선형 회귀를 수행합니다.

다음으로 선형 회귀를 수행하겠습니다. Stat를 누른 다음 CALC 로 스크롤합니다. 그런 다음 8: Linreg(a+bx) 로 스크롤하고 Enter 를 누릅니다.

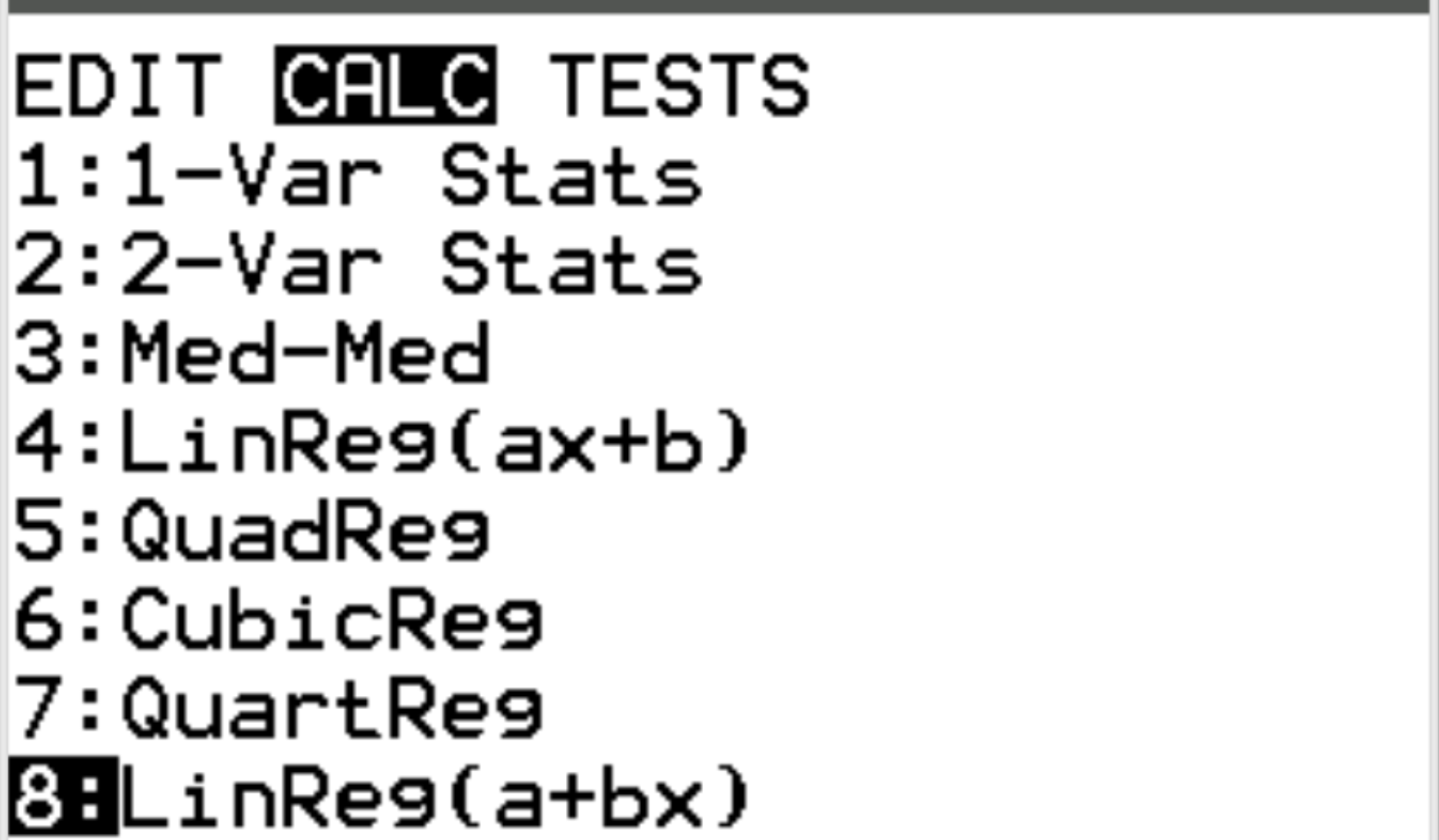
Xlist 및 Ylist의 경우 데이터를 입력하는 데 사용한 열인 L1 및 L2가 선택되었는지 확인하십시오. FreqList를 비워 두세요. 계산 까지 아래로 스크롤하고 Enter 키를 누릅니다. 다음 출력이 자동으로 나타납니다.

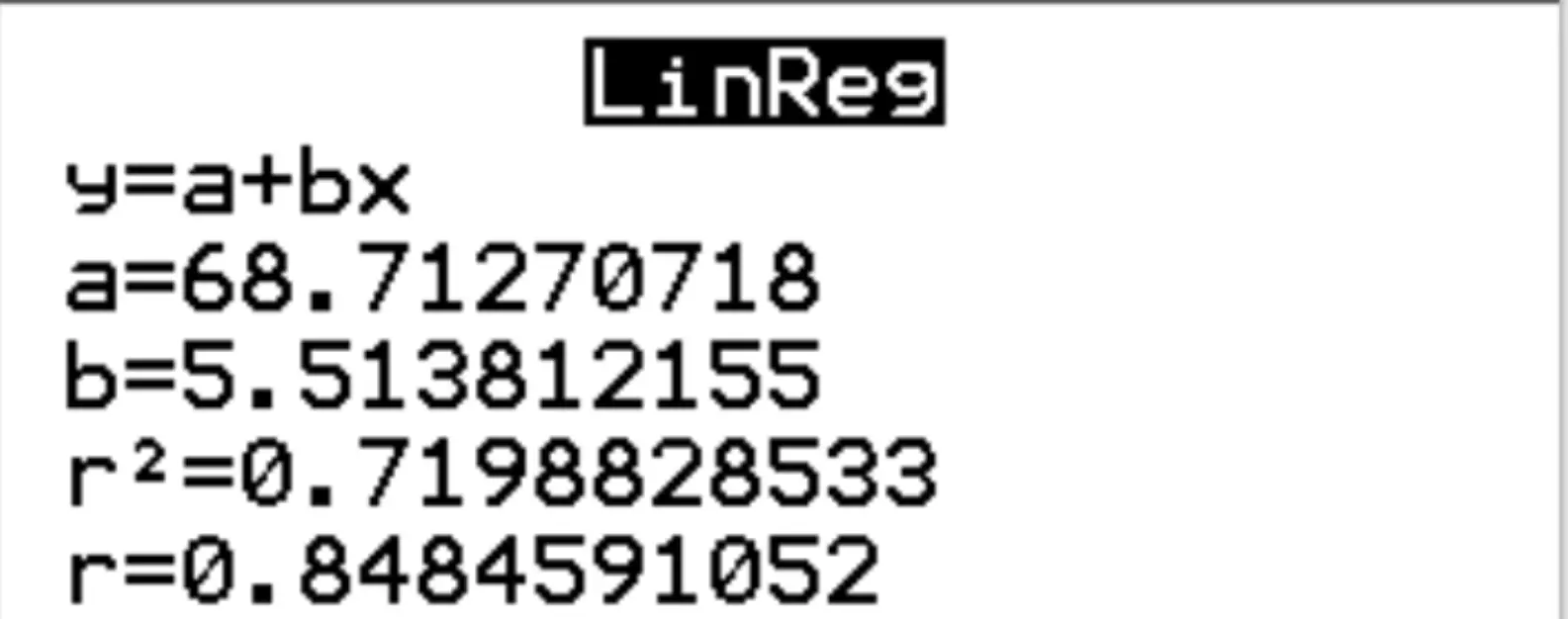
3단계: 결과를 해석합니다.

결과로부터 추정된 회귀 방정식은 다음과 같다는 것을 알 수 있습니다.

시험 점수 = 68.7127 + 5.5138*(시간)

우리는 시간 계수를 공부한 추가 시간마다 시험 점수가 평균 5.5138 씩 증가해야 함을 의미하는 것으로 해석합니다. 절편 계수는 0시간 공부하는 학생의 예상 시험 점수가 68.7127 이라는 의미로 해석됩니다.

이 추정 회귀 방정식을 사용하여 학습 시간을 기준으로 학생의 예상 시험 점수를 계산할 수 있습니다.

예를 들어, 3시간 동안 공부한 학생은 시험 점수 85.25 를 달성해야 합니다.

시험 점수 = 68.7127 + 5.5138*(3) = 85.25

또한 회귀 모델의 r 제곱은 r ² = 0.7199 임을 알 수 있습니다.

이 값을 결정계수라고 합니다. 설명변수로 설명할 수 있는 반응변수의 분산 비율입니다. 이 예에서는 시험 점수 변동의 71.99%가 공부 시간으로 설명될 수 있습니다.

추가 리소스

TI-84 계산기에서 잔차 플롯을 만드는 방법
TI-84 계산기에서 2차 회귀를 수행하는 방법
TI-84 계산기에서 지수 회귀를 수행하는 방법
TI-84 계산기에서 대수 회귀를 수행하는 방법