Sas에서 요리 거리를 계산하는 방법

Cook의 거리는 회귀 모델에서 영향력 있는 관측치를 식별하는 데 사용됩니다.

Cook의 거리 공식은 다음과 같습니다.

d _i = (ri ₂ / p*MSE) * (h _ii / (1-h _ii ^{) 2} )

금:

• r _i 는 i ^번째 잔기이다
• p 는 회귀 모델의 계수 수입니다.
• MSE 는 평균 제곱 오차입니다.
• h _ii 는 ^i번째 레버리지 값입니다.

기본적으로 Cook의 거리는 i ^번째 관측치가 제거될 때 모델의 모든 적합치가 얼마나 변경되는지 측정합니다.

Cook의 거리 값이 클수록 주어진 관측값의 영향력이 커집니다.

일반적으로 Cook 거리가 4/n( n = 총 관측치)보다 큰 관측치는 큰 영향을 미치는 것으로 간주됩니다.

다음 예에서는 SAS의 회귀 모델에서 각 관측값에 대한 Cook의 거리를 계산하는 방법을 보여줍니다.

예: SAS에서 요리사의 거리 계산

SAS에 다음과 같은 데이터 세트가 있다고 가정해 보겠습니다.

 /*create dataset*/
data my_data;
    input xy;
    datalines ;
8 41
12 42
12 39
13 37
14 35
16 39
17 45
22 46
24 39
26 49
29 55
30 57
;
run ;

/*view dataset*/
proc print data =my_data;

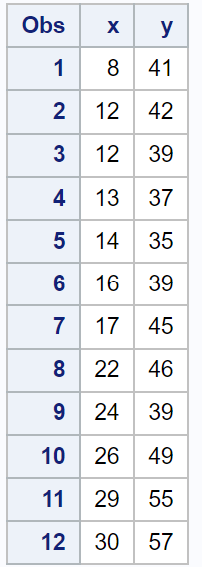
PROC REG를 사용하여 간단한 선형 회귀 모델을 이 데이터 세트에 맞춘 다음 COOKD 문과 함께 OUTPUT 문을 사용하여 회귀 모델의 각 관측값에 대한 Cook의 거리를 계산할 수 있습니다.

 /*fit simple linear regression model and calculate Cook's distance for each obs*/
proc reg data =my_data;
    model y=x;
    output out=cooksData cookd =cookd;
run ;

/*print Cook's distance values for each observation*/
proc print data =cooksData;

최종 결과 테이블에는 각 관측값에 대한 Cook 거리와 함께 원본 데이터세트가 표시됩니다.

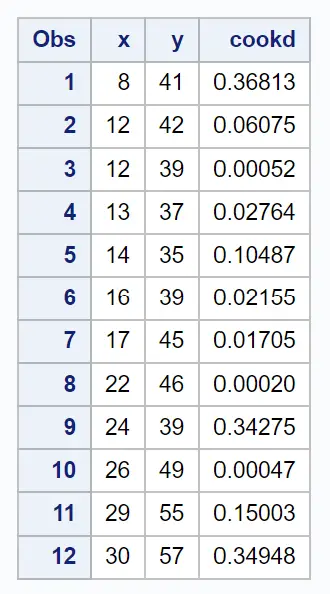
예를 들어 다음을 볼 수 있습니다.

• 첫 번째 관측값의 Cook 거리는 0.36813 입니다.
• 두 번째 관측치의 Cook 거리는 0.06075 입니다.
• 세 번째 관측치의 Cook 거리는 0.00052 입니다.

등등.

PROC REG 절차는 출력에 여러 진단 플롯도 생성하며 Cook 거리 플롯은 이 출력에서 볼 수 있습니다.

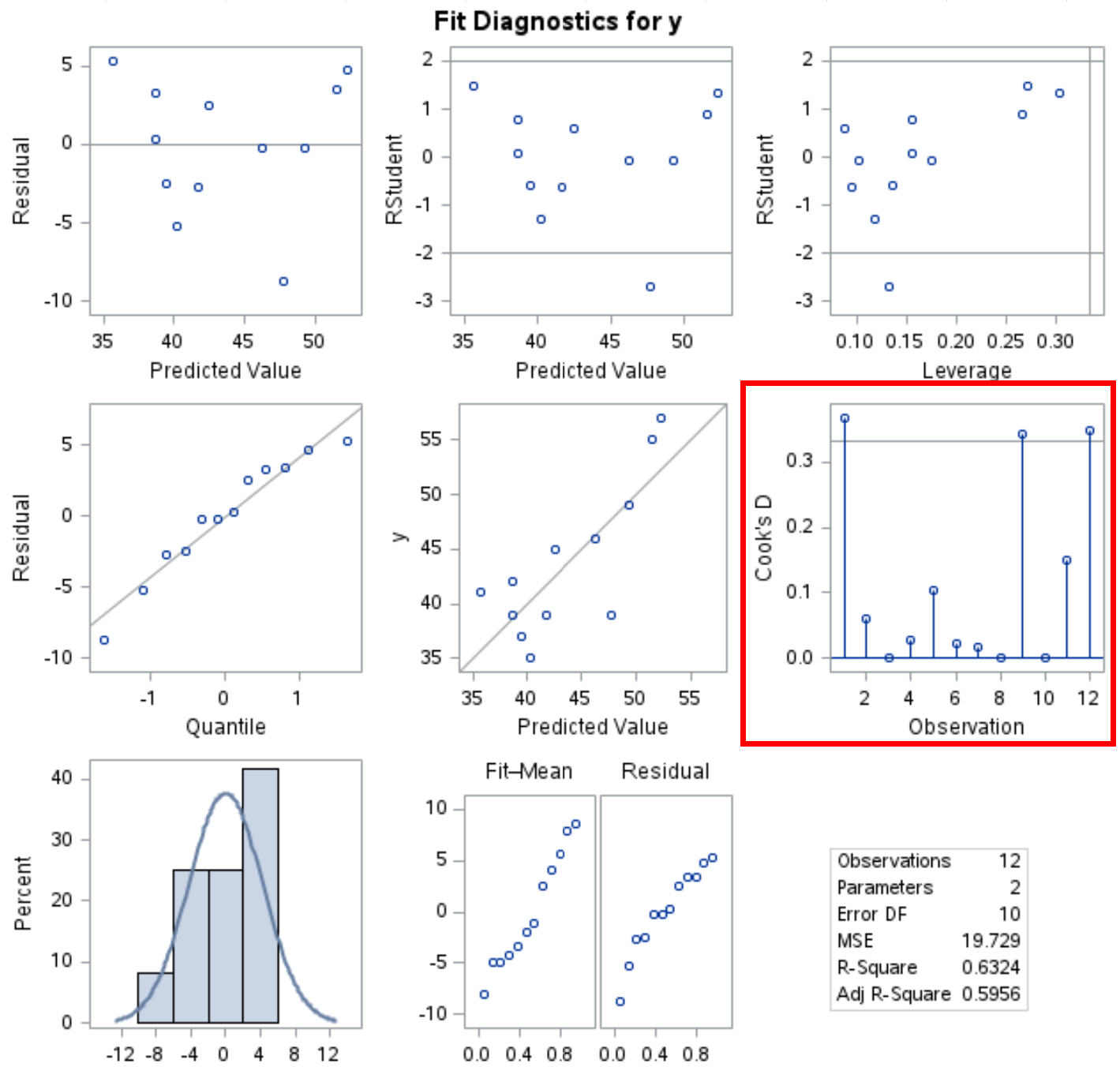
x축은 관측치 수를 나타내고 y축은 각 관측치에 대한 Cook 거리를 나타냅니다.

컷오프 선은 4/n(이 경우 n = 12이므로 컷오프는 0.33임)에 배치되며 데이터 세트의 세 관측치가 이 선보다 크다는 것을 알 수 있습니다.

이는 이러한 관찰이 회귀 모델에 큰 영향을 미칠 수 있으며 모델 결과를 해석하기 전에 더 자세히 조사해야 함을 나타냅니다.

추가 리소스

다음 튜토리얼에서는 SAS에서 다른 일반적인 작업을 수행하는 방법을 설명합니다.

SAS에서 잔차 그림을 만드는 방법
SAS에서 히스토그램을 만드는 방법
SAS에서 포인트 클라우드를 만드는 방법
SAS에서 이상값을 식별하는 방법