Sas에서 양방향 anova를 수행하는 방법

양방향 ANOVA는 두 변수(때때로 “요인”이라고도 함)에 할당된 세 개 이상의 독립 그룹 평균 간에 통계적으로 유의미한 차이가 있는지 여부를 확인하는 데 사용됩니다.

이 튜토리얼에서는 SAS에서 양방향 ANOVA를 수행하는 방법에 대한 단계별 예를 제공합니다.

1단계: 데이터 생성

식물학자가 식물의 성장이 햇빛에 대한 노출과 물주기의 빈도에 의해 영향을 받는지 알고 싶어한다고 가정해 보겠습니다.

그녀는 30개의 씨앗을 심고 햇빛 노출과 물 주기 등 다양한 조건에서 한 달 동안 자라게 합니다. 한 달 후에 그녀는 각 식물의 높이를 기록합니다. 결과는 아래와 같습니다:

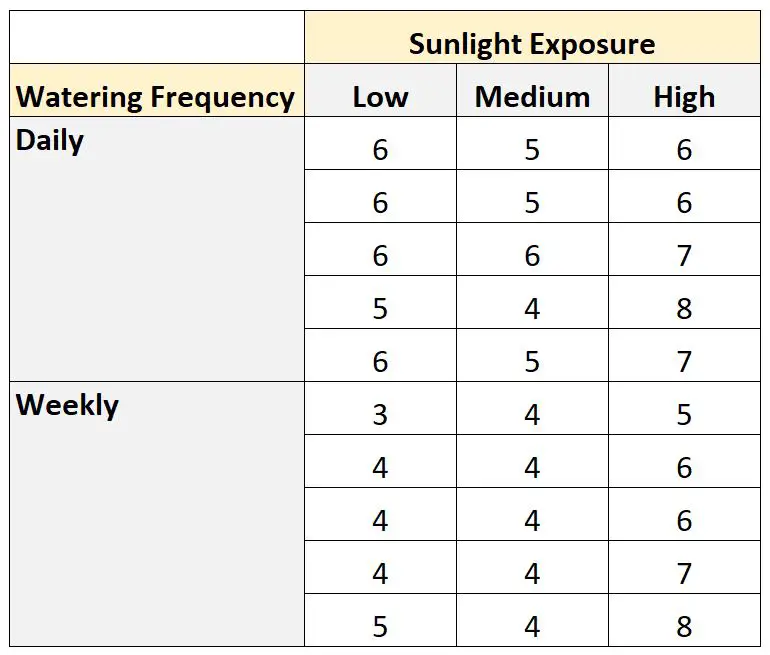
다음 코드를 사용하여 SAS에서 이 데이터 세트를 생성할 수 있습니다.

 /*create dataset*/
data my_data;
    input water $sunlight $height;
    datalines ;
daily low 6
daily low 6
daily low 6
daily low 5
daily low 6
daily med 5
daily med 5
daily med 6
daily med 4
daily med 5
daily high 6
daily high 6
daily high 7
daily high 8
daily high 7
weekly low 3
weekly low 4
weekly low 4
weekly low 4
weekly low 5
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly med 4
weekly high 5
weekly high 6
weekly high 6
weekly high 7
weekly high 8
;
run ;

2단계: 양방향 ANOVA 수행

다음으로 proc ANOVA를 사용하여 양방향 ANOVA를 수행하겠습니다.

 /*perform two-way ANOVA*/
proc ANOVA data =my_data;
class water sunlight;
model height = water sunlight water*sunlight;
means water sunlight / tukey cldiff ;
run ;

3단계: 결과 해석

결과에서 분석하려는 첫 번째 테이블은 ANOVA 테이블입니다.

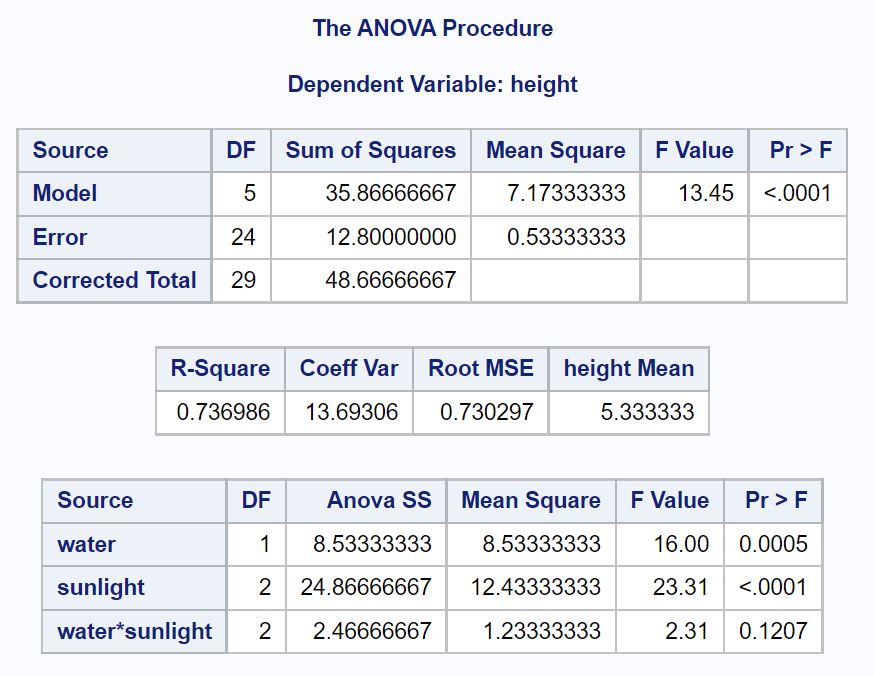
이 표에서 우리는 다음을 볼 수 있습니다:

• 물에 대한 p-값: 0.0005
• 햇빛에 대한 p-값: <.0001
• 물과 햇빛 사이의 상호작용에 대한 p-값: . 1207

이는 물과 햇빛이 식물의 키를 통계적으로 유의하게 예측하고 물과 햇빛 사이에 통계적으로 유의미한 상호작용 효과가 없다는 것을 말해줍니다.

다음으로 Tukey의 사후 테스트 결과를 조사하여 어떤 물과 햇빛 수준이 통계적으로 유의하게 다른지 확인할 수 있습니다.

먼저, 물에 대한 Tukey의 사후 비교를 살펴보겠습니다.

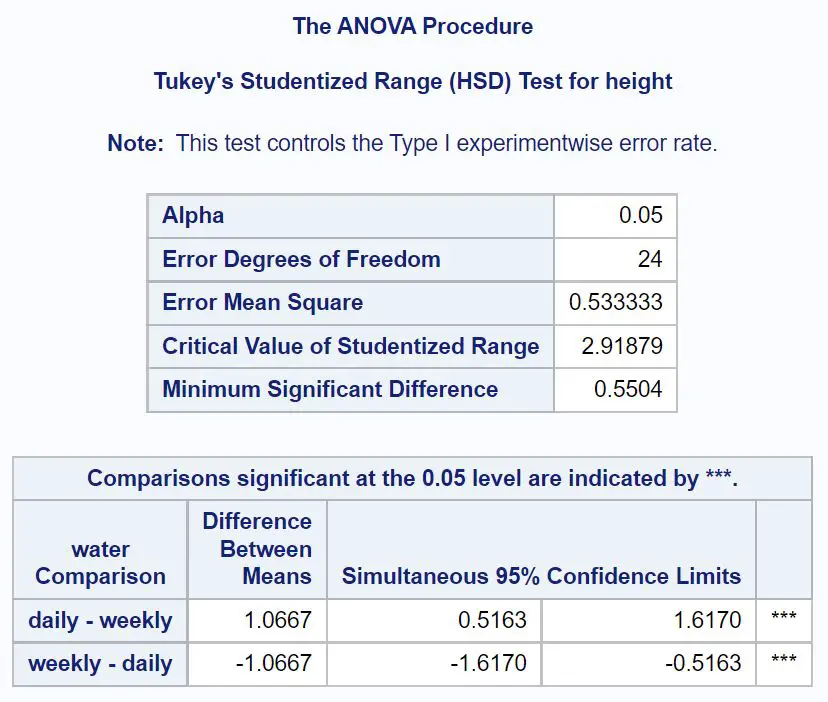
결과에서 우리는 매일 물을 주는 식물과 매주 물을 주는 식물 사이의 평균 높이 차이가 1.0667 인치임을 알 수 있습니다.

평균 크기의 차이에 대한 95% 신뢰 구간은 [.5163, 1.6170] 입니다. 이는 매일 물을 주는 식물과 매주 물을 주는 식물 사이의 평균 높이의 실제 차이가 0.5163인치에서 1.6170인치 사이라는 것을 95% 확신한다는 것을 의미합니다.

먼저, 햇빛에 대한 Tukey의 사후 비교를 살펴보겠습니다.

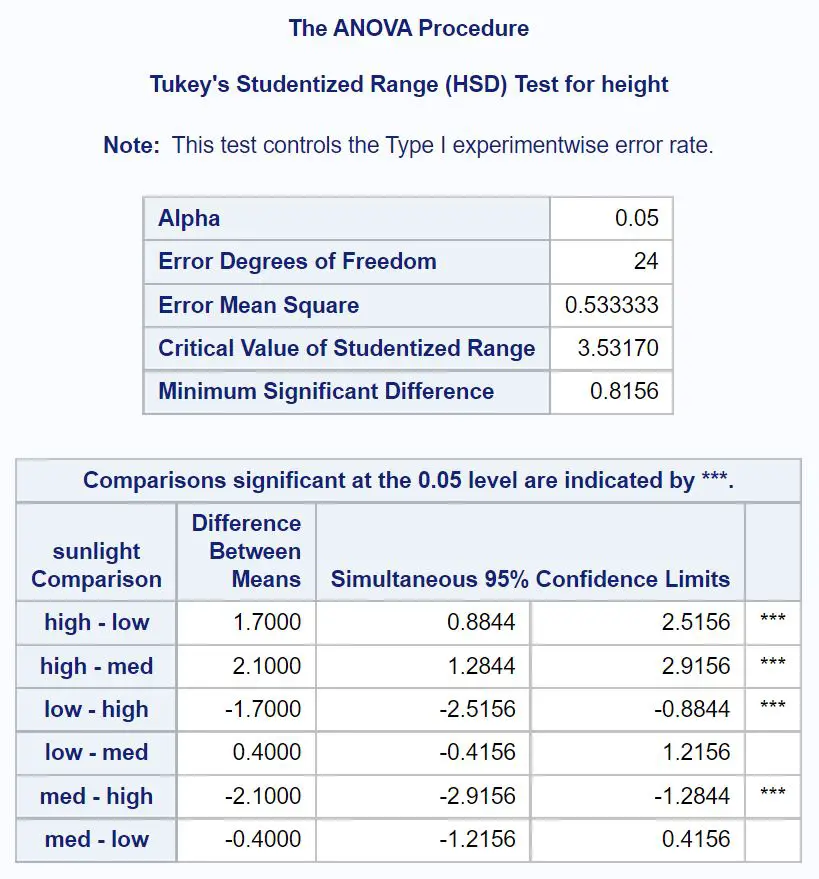
어떤 그룹 평균이 다른지 확인하려면 옆에 별표( *** )가 있는 쌍별 비교를 살펴봐야 합니다.

표에서 다음 그룹의 평균이 통계적으로 유의미하게 다르다는 것을 알 수 있습니다.

• 높은 일조량 또는 낮은 일조량(95% CI = [.8844, 2.5156])
• 높은 일조량 또는 중간 정도의 일조량(95% CI = [1.2844, 2.9156])

4단계: 결과 보고

마지막으로 양방향 ANOVA의 결과를 보고 할 수 있습니다.

물 공급 빈도와 태양 노출이 식물 성장에 미치는 영향을 분석하기 위해 양방향 ANOVA를 수행했습니다.

양방향 ANOVA는 물 주기와 태양 노출의 효과 사이에 통계적으로 유의미한 상호 작용이 없음을 보여주었습니다(p = 0.1207).

간단한 손 효과 분석에서는 물주기가 식물 성장에 통계적으로 유의미한 영향을 미치는 것으로 나타났습니다(p = 0.0005).

간단한 손 효과 분석에서는 태양 노출도 식물 성장에 통계적으로 유의미한 영향을 미치는 것으로 나타났습니다(p < 0.0001).

추가 리소스

다음 자습서에서는 양방향 분산 분석에 대한 추가 정보를 제공합니다.

양방향 분산 분석 소개
일원 분산 분석 또는 양방향 분산 분석: 언제 사용합니까?
양방향 ANOVA를 수동으로 수행하는 방법