Excel에서 예측 구간을 구성하는 방법

통계에서 단순 선형 회귀는 예측 변수 x와 반응 변수 y 사이의 관계를 수량화하는 데 사용할 수 있는 기술입니다.

단순 선형 회귀를 수행하면 x와 y 사이의 관계를 설명하는 “최적 적합선”을 얻습니다. 이는 다음과 같이 작성할 수 있습니다.

ŷ = _b0 + _b1x

금:

• ŷ는 반응 변수의 예측값입니다.
• b _0은 y 절편입니다.
• b ₁ 은 회귀 계수입니다.
• x는 예측 변수의 값입니다.

때때로 우리는 주어진 x ₀ 값에 대한 예측 구간을 구성하기 위해 이 최적선을 사용하기를 원합니다. 이는 모집단에서 y의 실제 값이 95% 확률로 존재하는 예측 값 ŷ ₀ 주위의 구간입니다. x ₀ 에 해당하는 부분이 이 간격에 포함됩니다.

주어진 값 x ₀ 에 대한 예측 구간을 계산하는 공식은 다음과 같습니다.

ŷ ₀ +/- t _α/2,df=n-2 * se

금:

se = S _yx √(1 + 1/n + (x ₀ – x ) ² /SS _x )

공식이 조금 어려워 보일 수도 있지만 실제로 Excel에서 계산하는 것은 간단합니다. 다음으로 이 수식을 사용하여 Excel에서 특정 값에 대한 예측 구간을 계산하는 예를 살펴보겠습니다.

예: Excel에서 예측 구간을 구성하는 방법

다음 데이터세트는 15명의 학생이 얻은 시험 점수와 공부한 시간을 보여줍니다.

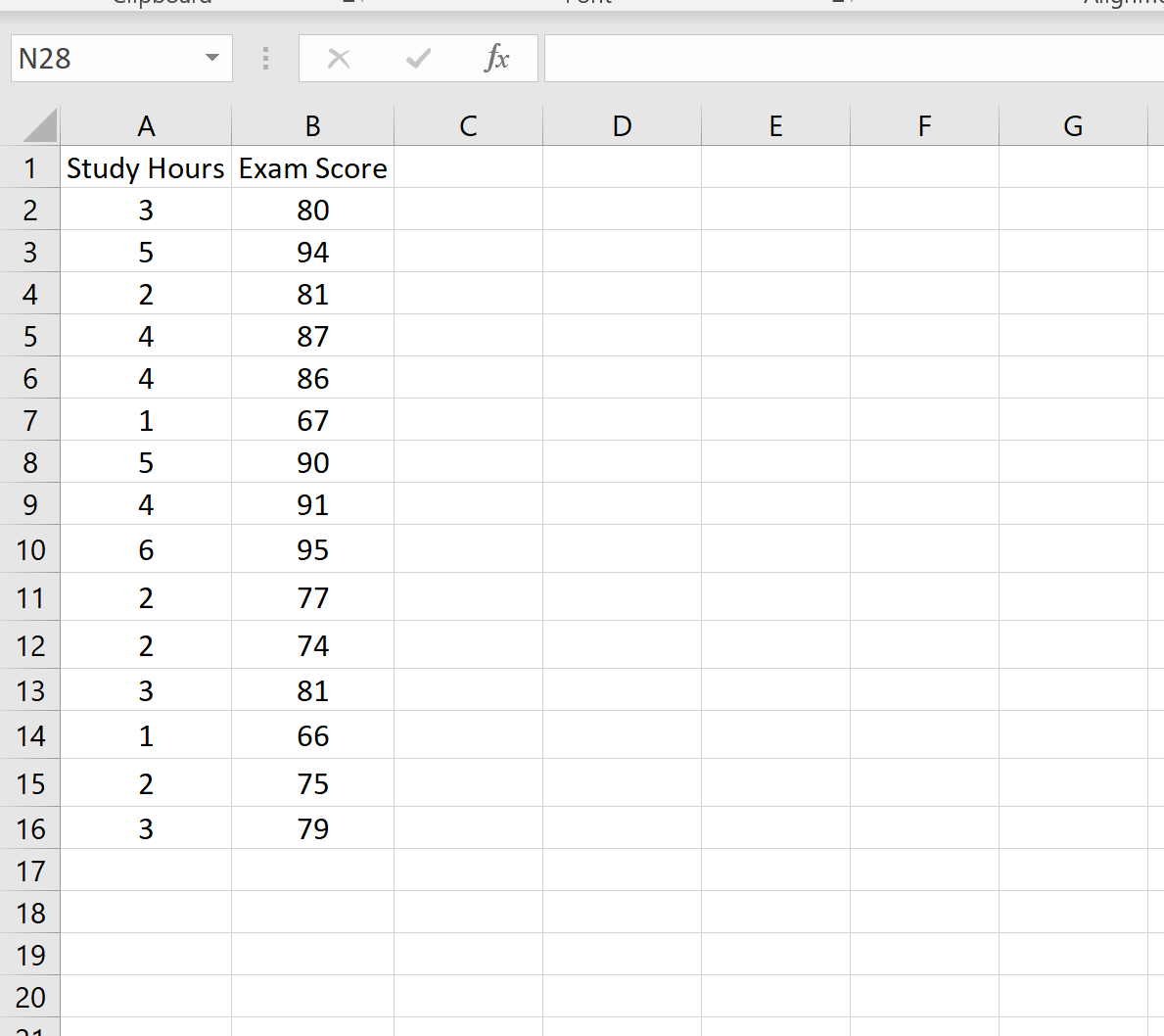
x ₀ = 3 값에 대해 95% 예측 구간을 생성한다고 가정합니다. 즉, 공부하는 학생의 시험 점수가 이 구간 내에 포함될 확률이 95%가 되도록 구간을 생성하려고 합니다. 3 시간.

다음 스크린샷은 이 예측 구간을 얻는 데 필요한 모든 값을 계산하는 방법을 보여줍니다.

참고: F 열의 수식은 E 열의 값이 어떻게 계산되었는지 보여줍니다.

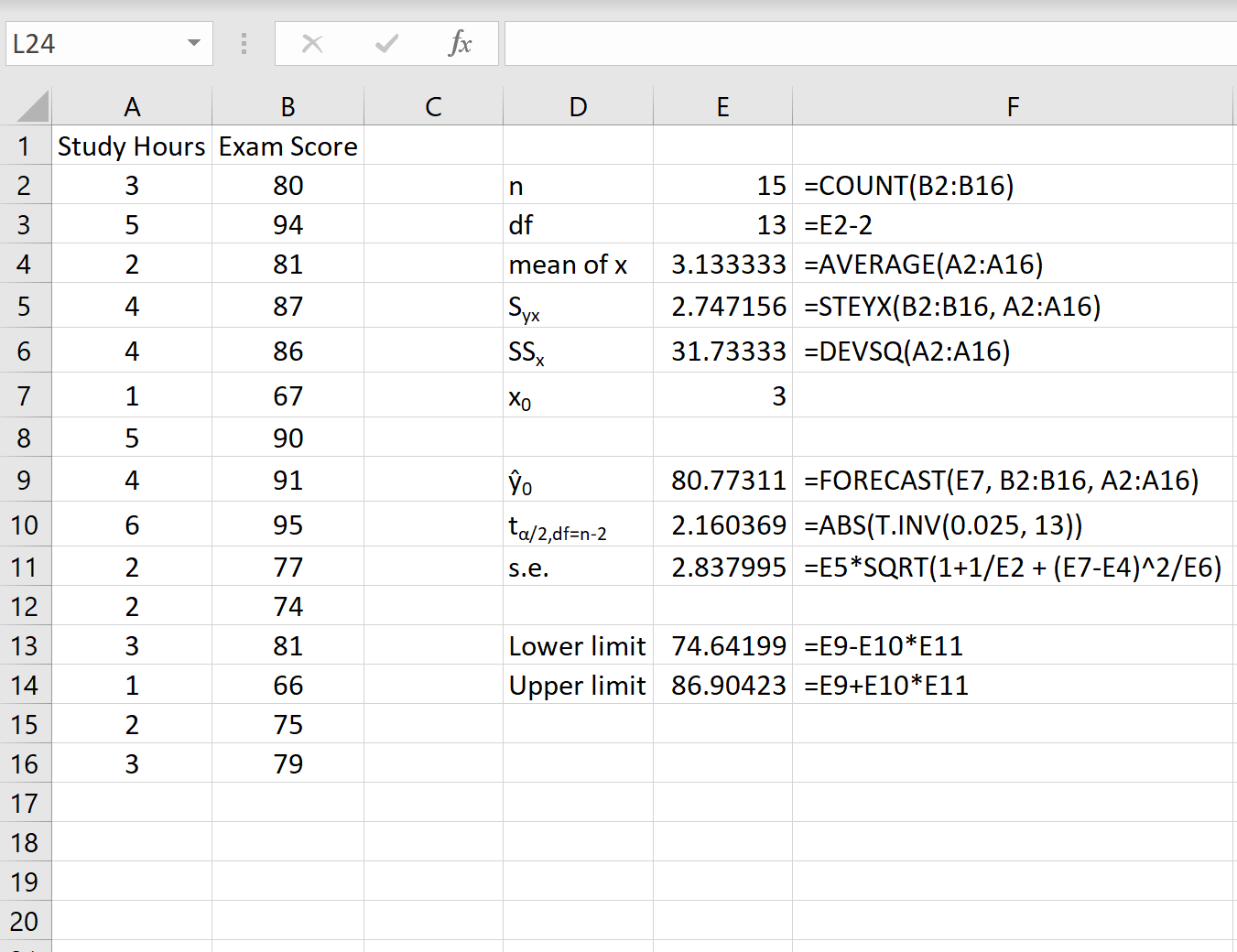
x ₀ = 3 값에 대한 95% 예측 구간은 (74.64, 86.90) 입니다. 즉, 3시간 공부한 학생이 74.64~86.90 사이의 점수를 얻을 확률을 95%로 예측한다.

사용된 계산에 대한 몇 가지 참고 사항:

• t _α/2,df=n-2 의 t 임계값을 계산하기 위해 우리는 95%의 예측 구간을 원했기 때문에 α/2 = 0.05/2 = 0.25를 사용했습니다. 예측 구간이 높을수록(예: 99% 예측 구간) 구간이 더 넓어집니다. 반대로, 예측 구간이 작을수록(예: 90% 예측 구간) 구간이 더 좁아집니다.
• ŷ ₀ 에 대한 예측값을 얻기 위해 =FORECAST() 공식을 사용했지만 =FORECAST.LINEAR() 공식은 정확히 동일한 값을 반환합니다.