타자

에 의해 벤자민 앤더슨 8월 5, 2023 통계 댓글 0개

이 문서에서는 통계에서 분포를 특성화하는 것이 무엇을 의미하는지 설명합니다. 따라서 유형화의 정의, 변수 유형화의 예를 찾을 수 있으며, 또한 단계별로 해결하는 연습문제를 통해 연습할 수 있습니다.

타이핑이란 무엇입니까?

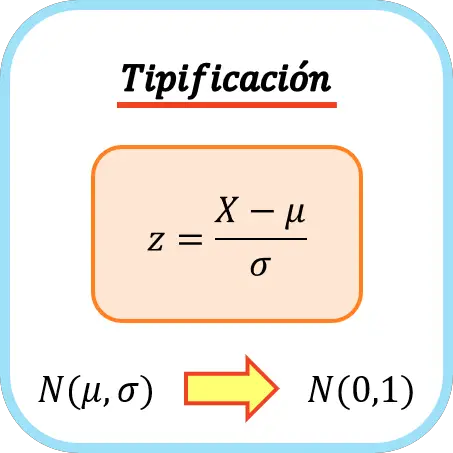
통계에서 정규화는 평균과 표준 편차가 각각 0과 1이 되도록 분포에 선형 변환을 적용하는 프로세스입니다.

보다 정확하게는 타이핑에는 무작위 변수에서 평균을 뺀 다음 이를 표준편차로 나누는 작업이 포함됩니다.

타이핑은 정규화(normalization) 또는 표준화(standardization)라고도 합니다.

입력식

변수를 분류하려면 평균을 뺀 다음 표준편차로 나누어야 합니다. 따라서 변수를 입력하는 공식은 다음과 같습니다.

금

$\mu$

변수의 평균이다

$X$

그리고

$\sigma$

표준편차(또는 표준편차)입니다.

따라서 선형 변환이 변수에 적용되므로 항목은 실제로 변수 변경입니다.

예시 항목

유형화의 정의와 그 공식을 고려하면, 개념을 완전히 이해하기 위한 구체적인 예는 다음과 같습니다.

연속 확률 변수는 평균이 45이고 표준 편차가 10인 정규 분포를 따릅니다. 60보다 작거나 같은 값을 얻을 확률은 얼마입니까?

$N(45,10)$

정규분포의 확률을 찾으려면 특성표를 사용해야 하지만, 이를 위해서는 먼저 타이핑 과정을 수행해야 합니다. 따라서 평균을 빼고 표준편차로 확률값을 나눕니다.

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

표준화한 후에는 정규 분포 확률표로 이동하여 1.5 값이 어떤 확률에 해당하는지 확인합니다.

정규분포 유형화 표에서 볼 수 있듯이, 이전 단계에서 계산된 값은 다음 확률에 해당합니다.

$\displaystyle P(Z\leq 1,5)=0,9332$

따라서 60 이하의 값을 얻을 확률은 93.32%입니다.

타이핑 연습 해결

평균과 표준편차가 각각 120과 50인 정규분포의 다음 확률을 계산합니다.

$N(120,50)$

208 이하의 값을 얻을 확률입니다.
137보다 큰 값을 얻을 확률입니다.

솔루션 보기

문제의 두 섹션 모두에서 확률을 계산하려면 정규 분포를 입력해야 합니다.

208보다 작거나 같은 값의 확률 입력을 계산하는 것부터 시작합니다.

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

이제 위의 표에서 값 1.76이 어떤 확률에 해당하는지 살펴보겠습니다.

$\displaystyle P(Z\leq 1,76)=0,9608$

둘째, 137보다 큰 값을 얻을 확률을 계산합니다. 같은 방식으로 변수를 입력하는 것으로 시작합니다.

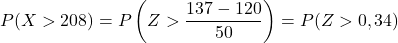$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”398″ style=”vertical-align: -17px;”> <p class=$ 그러나 첨부된 테이블은 누적 확률이 가장 낮으므로 테이블을 사용하려면 먼저 확률을 변환해야 합니다.

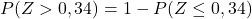$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”252″ style=”vertical-align: -5px;”> <p class=$ 그리고 마지막으로 계산된 Z 값에 해당하는 확률을 첨부된 표에서 확인하겠습니다.

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”435″ style=”vertical-align: -5px;”> <div class=$

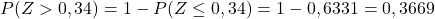
타이핑의 요점은 무엇입니까?

유형화의 의미를 완전히 이해하기 위해 이것이 무엇을 위해 사용되는지, 언제 변수를 입력해야 하는지 살펴보겠습니다.

주로 표준화는 평균과 분산이 다른 분포 값을 비교하는 데 사용됩니다. 마찬가지로 표준화는 확률을 계산하는 데에도 사용됩니다.

서로 다른 특성을 지닌 분포의 두 값을 표준화함으로써 전체 분포에 비해 어떤 값이 더 크거나 작은지를 알 수 있습니다. 즉, 유형화 과정을 적용하면 어떤 값이 그 분포의 평균에 가장 가깝거나 가장 먼지를 알 수 있습니다.

또한 위에서 설명한 대로 일반적으로 확률 테이블은 유형화된 분포를 기반으로 하기 때문에 유형화를 통해 확률 계산도 가능합니다.

저자 소개

벤자민 앤더슨

안녕하세요. 저는 통계학 교수를 퇴직하고 전임 통계 교사로 변신한 벤자민입니다. 통계 분야의 광범위한 경험과 전문 지식을 바탕으로 Statorials를 통해 학생들에게 힘을 실어주기 위해 지식을 공유하고 싶습니다. 더 알아보기