이항분포 소개

이항 분포는 통계학에서 가장 널리 사용되는 분포 중 하나입니다. 이항분포를 이해하려면 먼저 이항실험을 이해하는 것이 도움이 됩니다.

이항 실험

이항 실험은 다음과 같은 특성을 갖는 실험입니다.

• 실험은 n 번의 반복 시행으로 구성됩니다.
• 각 시행에는 두 가지 가능한 결과만 있습니다.
• p 로 표시되는 성공 확률은 각 시행마다 동일합니다.
• 각 테스트는 독립적입니다.

이항 실험의 가장 확실한 예는 동전 던지기입니다. 예를 들어, 동전을 10번 던졌다고 가정해 보겠습니다. 이는 다음과 같은 네 가지 속성을 갖기 때문에 이항 실험입니다.

• 실험은 n번의 반복 시행으로 구성됩니다. 즉, 10번의 시행이 있습니다.
• 각 시행에는 앞면 또는 뒷면이라는 두 가지 가능한 결과만 있습니다.
• p 로 표시되는 성공 확률은 각 시행마다 동일합니다. “성공”을 랜딩 헤드로 정의하면 각 시행에 대해 성공 확률은 정확히 0.5입니다.
• 각 시행은 독립적입니다. 한 번의 동전 던지기 결과는 다른 동전 던지기의 결과에 영향을 미치지 않습니다.

이항 분포

이항 분포는 n 번의 이항 실험에서 k번의 성공 확률을 나타냅니다.

확률 변수 X가 이항 분포를 따르는 경우 X = k 성공 확률은 다음 공식으로 찾을 수 있습니다.

P(X=k) = _n C _k * p ^k * (1-p) ^nk

금:

• n: 시행 횟수
• k: 성공 횟수
• p: 주어진 시행의 성공 확률
• _n C _k : n 번 시행에서 k번 성공하는 방법의 수

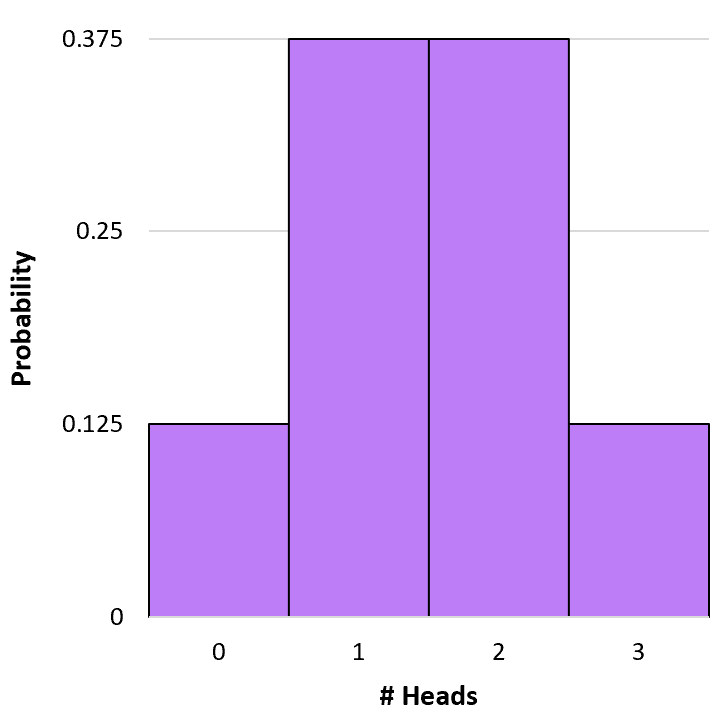
예를 들어 동전을 3번 던졌다고 가정해 보겠습니다. 위의 공식을 사용하여 3번의 던지기에서 앞면이 0, 1, 2, 3번 나올 확률을 결정할 수 있습니다.

P(X=0) = ₃ C ₀ * 0.5 ⁰ * (1-0.5) ^3-0 = 1 * 1 * (0.5) ³ = 0.125

P(X=1) = ₃ C ₁ * 0.5 ¹ * (1-0.5) ^3-1 = 3 * 0.5 * (0.5) ² = 0.375

P(X=2) = ₃ C ₂ * 0.5 ² * (1-0.5) ^3-2 = 3 * 0.25 * (0.5) ¹ = 0.375

P(X=3) = ₃ C ₃ * 0.5 ³ * (1-0.5) ^3-3 = 1 * 0.125 * (0.5) ⁰ = 0.125

참고 : 이 결합된 계산기를 사용하여 각 예 _{에 대한 nCk를} 계산 했습니다 .

이 확률 분포를 시각화하기 위해 간단한 히스토그램을 만들 수 있습니다.

누적 이항 확률 계산

위의 공식을 사용하여 단일 이항 확률(예: 동전을 3번 던지면 1번 앞면이 나올 확률)을 계산하는 것은 간단하지만 누적 이항 확률을 계산하려면 개별 확률을 추가해야 합니다.

예를 들어, 동전을 3번 던져서 앞면이 1번 이하로 나올 확률을 알고 싶다고 가정해 보겠습니다. 이 확률을 계산하기 위해 다음 공식을 사용합니다.

P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 .

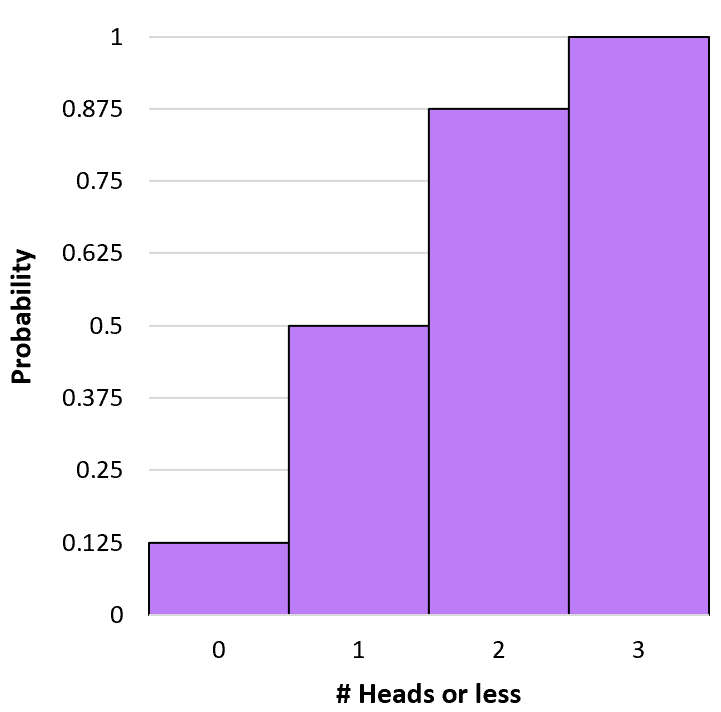
이는 여러 확률을 추가하는 것과 관련되므로 누적 확률 이라고 합니다. 비슷한 공식을 사용하여 각 결과에 대해 k 개 이하의 앞면이 나올 누적 확률을 계산할 수 있습니다.

P(X≤0) = P(X=0) = 0.125 .

P(X≤1) = P(X=0) + P(X=1) = 0.125 + 0.375 = 0.5 .

P(X≤2) = P(X=0) + P(X=1) + P(X=2) = 0.125 + 0.375 + 0.375 = 0.875 .

P(X≤3) = P(X=0) + P(X=1) + P(X=2) + P(X=3) = 0.125 + 0.375 + 0.375 + 0.125 = 1 .

이 누적 확률 분포를 시각화하기 위해 히스토그램을 만들 수 있습니다.

이항 확률 계산기

작은 숫자(예: 동전 3개 던지기)를 다룰 때는 이항 확률을 직접 계산하는 것이 합리적입니다. 그러나 더 큰 숫자(예: 100개의 무승부)로 작업할 때는 확률을 직접 계산하기 어려울 수 있습니다. 이러한 경우에는 아래와 같은 이항 확률 계산기를 사용하는 것이 도움이 될 수 있습니다.

예를 들어, 동전을 n = 100번 던졌고, 주어진 시행에서 앞면이 나올 확률은 p = 0.5이고, 앞면이 k = 43번 이하로 나올 확률을 알고 싶다고 가정합니다.

결과를 해석하는 방법은 다음과 같습니다.

• 동전이 정확히 43번 나올 확률은 0.03007 입니다.
• 동전이 43번 미만으로 앞면이 나올 확률은 0.06661 입니다.
• 동전이 앞면이 43번 이하로 나올 확률은 0.09667 입니다.
• 동전이 43번 이상 앞면이 나올 확률은 0.90333 입니다.
• 동전이 앞면이 43번 이상 나올 확률은 0.93339 입니다.

이항 분포의 속성

이항 분포에는 다음과 같은 속성이 있습니다.

분포의 평균은 μ = np 입니다.

분포의 분산은 σ ² = np(1-p) 입니다.

분포의 표준편차는 σ = √ np(1-p) 입니다.

예를 들어, 동전을 세 번 던졌다고 가정해 보겠습니다. p = 동전이 앞면이 나올 확률이라고 하자.

우리가 예상하는 평균 앞면 수는 μ = np = 3*.5 = 1.5 입니다.

우리가 기대하는 인원수 분산은 σ ² = np(1-p) = 3*.5*(1-.5) = 0.75 입니다.

이항 분포 연습 문제

다음 연습 문제를 사용하여 이항 분포에 대한 지식을 테스트하세요.

문제 1

질문: 밥은 자유투 시도의 60%를 성공시켰습니다. 만약 그가 12번의 자유투를 성공했다면, 그가 정확히 10번의 자유투를 성공할 확률은 얼마입니까?

답변: 위의 이항 분포 계산기를 p = 0.6, n = 12 및 k = 10으로 사용하면 P(X=10) = 0.06385 라는 것을 알 수 있습니다.

문제 2

질문: 제시카는 동전을 5번 던졌습니다. 동전이 앞면이 2번 이하로 나올 확률은 얼마입니까?

답변: 위의 이항 분포 계산기를 p = 0.5, n = 5, k = 2로 사용하면 P(X≤2) = 0.5 라는 것을 알 수 있습니다.

문제 3

질문: 특정 학생이 특정 대학에 합격할 확률은 0.2입니다. 10명이 지원한다면 4명 이상이 합격할 확률은 얼마나 됩니까?

답변: 위의 이항 분포 계산기를 p = 0.2, n = 10 및 k = 4로 사용하면 P(X>4) = 0.03279 라는 것을 알 수 있습니다.

문제 4

질문: 동전을 12번 던졌습니다. 나타날 것으로 예상되는 평균 앞면 수는 얼마입니까?

답변: 이항 분포의 평균은 μ = np로 계산된다는 점을 기억하세요. 따라서 μ = 12*0.5 = 6개의 앞면이 됩니다 .

문제 5

질문: 마크는 자신의 시도 중 10%에서 홈런을 쳤습니다. 주어진 경기에서 그가 5번의 시도를 했다면 그가 친 홈런 수의 변화는 얼마나 됩니까?

답변: 이항 분포의 분산은 σ ² = np(1-p)로 계산된다는 점을 기억하세요. 따라서 ^σ2 = 6*.1*(1-.1) = 0.54 입니다.

추가 리소스

다음 기사는 다양한 통계 소프트웨어에서 이항 분포를 사용하는 방법을 배우는 데 도움이 될 수 있습니다.

• Excel에서 이항 확률을 계산하는 방법
• TI-84 계산기에서 이항 확률을 계산하는 방법
• R에서 이항 확률을 계산하는 방법
• R에서 이항 분포를 그리는 방법