이항 분포
이 기사에서는 통계에서 이항 분포가 무엇인지, 그리고 그것이 무엇을 위해 사용되는지 설명합니다. 따라서 이항 분포의 정의, 이항 분포의 예 및 이러한 유형의 확률 분포의 속성을 찾을 수 있습니다. 또한 온라인 계산기를 사용하여 이항 분포의 확률을 계산할 수 있습니다.
이항 분포란 무엇입니까?
이항 분포는 일정한 성공 확률을 사용하여 일련의 독립적인 이분법적 실험을 수행할 때 성공 횟수를 계산하는 확률 분포입니다.
즉, 이항 분포는 일련의 베르누이 시행에서 성공적인 결과의 수를 설명하는 분포입니다.
베르누이 테스트는 “성공”과 “실패”라는 두 가지 결과를 얻을 수 있는 실험이라는 점을 기억하세요. 따라서 “성공” 확률이 p 라면 “실패” 확률은 q=1-p 입니다.
일반적으로 수행된 총 실험 수는 매개변수 n 으로 정의되며, p 는 각 실험의 성공 확률입니다. 따라서 이항 분포를 따르는 확률 변수는 다음과 같이 작성됩니다.
![]()
이항 분포에서는 완전히 동일한 실험이 n 번 반복되고 실험이 서로 독립적이므로 각 실험의 성공 확률은 동일합니다 (p) .
이항 분포는 이항 분포 라고도 합니다.
이항 분포의 예
이항 분포의 정의를 살펴본 후에는 개념을 더 잘 이해하기 위해 이러한 유형의 분포를 따르는 변수의 몇 가지 예를 살펴보겠습니다.
- 동전을 25번 던졌을 때 앞면이 나오는 횟수입니다.
- 농구 선수가 같은 위치에서 골대를 향해 60번 슛을 날렸을 때 찍은 슛의 수입니다.
- 주사위를 30번 굴려 숫자 6이 나온 횟수입니다.
- 시험에 응시하는 총 50명의 학생 중 합격한 수입니다.
- 100개 제품의 표본에 포함된 불량 단위의 수입니다.
이항 분포 공식
매개변수 x, n, p가 주어지면 이항 분포의 확률 함수는 x 곱하기 p x 곱하기 (1-p) nx 의 n 조합 수로 정의됩니다.
따라서 이항 분포의 확률을 계산하는 공식은 다음과 같습니다.

👉 아래 계산기를 사용하여 이항 분포를 따르는 변수의 확률을 계산할 수 있습니다.
한편, 이항 분포의 누적 확률은 해당 성공 사례 수의 확률과 이전의 모든 확률을 더하여 계산됩니다. 따라서 이항 분포의 누적 확률을 계산하는 공식은 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e31ef4ae023b8bf51c0b6816bc787c91_l3.png)
이항 분포에 대한 해결 연습
- 동전을 10번 던졌을 때 앞면이 6번 나올 확률은 얼마입니까?
이 문제의 변수는 모든 출시가 서로 독립적이고 동일한 성공 확률을 갖기 때문에 이항 분포를 따릅니다.
구체적으로, 두 가지 가능한 결과 중 하나만 성공으로 간주되므로 성공 확률은 50%입니다.
![]()
따라서 이 연습의 분포는 총 10번의 실험과 0.5의 확률을 갖는 이항 분포입니다.
![]()
따라서 앞면이 6개 나올 확률을 결정하려면 이항 분포 공식을 적용해야 합니다.
![Rendered by QuickLaTeX.com \begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-17346d59c641378880b734dfe88210f6_l3.png)
따라서 동전을 10번 던져서 앞면이 정확히 6번 나올 확률은 20.51%입니다.
이항분포의 특성
이항 분포에는 다음과 같은 특징이 있습니다.
- 이항 분포는 두 개의 매개변수로 정의됩니다. n 은 베르누이 실험의 총 횟수이고, p 는 각 베르누이 실험의 성공 확률입니다.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cd9728a237a5f49107bf14f440620936_l3.png)
- 이항 분포의 평균은 총 실험 수에 각 실험의 성공 확률을 곱한 것과 같습니다. 따라서 이항 분포의 평균을 계산하려면 n 에 p를 곱해야 합니다.
![]()
- 이항 분포의 분산은 총 시행 횟수에 성공 확률과 실패 확률을 곱한 값과 같습니다.
![]()
- 이항 분포의 확률 함수 공식은 다음과 같습니다.
![]()
- 마찬가지로, 이항 분포의 누적 분포 함수에 대한 공식은 다음과 같습니다.
![Rendered by QuickLaTeX.com \displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e31ef4ae023b8bf51c0b6816bc787c91_l3.png)
- 동일한 확률을 갖는 두 개의 독립적인 이항 분포의 합은 동일한 확률 값 p 를 갖는 이항 분포와 동일하며 n 은 두 분포의 총 시행 횟수의 합입니다.
![Rendered by QuickLaTeX.com \begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-dbc1a01b2d5654864d688cc46ac3a2e6_l3.png)
![]()
- 베르누이 분포는 n=1 인 이항 분포의 특별한 경우입니다. 즉, 단 한 번의 실험만 수행됩니다.
![]()
- X 1 , X 2 ,…, X k 가 다음과 같은 독립 확률 변수인 경우
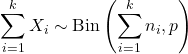
이항 분포 계산기
이항분포의 매개변수 p, n , x 의 값을 다음 계산기에 입력하여 확률을 계산합니다. 계산하려는 확률을 선택하고 점을 소수 구분 기호로 사용하여 숫자를 입력해야 합니다(예: 0.1667).