Ti-84 계산기에서 invnorm을 사용하는 방법(예제 포함)

TI-84 계산기의 invNorm() 함수를 사용하여 정규 분포 와 관련된 z개의 임계 값을 찾을 수 있습니다.

이 함수는 다음 구문을 사용합니다.

invNorm(확률, μ, σ)

금:

• 확률: 유의 수준
• μ: 인구 평균
• σ: 모집단 표준편차

TI-84 계산기에서 2nd를 누른 다음 VARS를 눌러 이 기능에 액세스할 수 있습니다. 그러면 invNorm() 을 사용할 수 있는 DISTR 화면으로 이동합니다.

다음 예에서는 이 기능을 실제로 사용하는 방법을 보여줍니다.

예 1: 단측 검정의 임계 Z 값

연구자가 α = 0.05를 사용하여 왼손잡이 가설 검정을 수행한다고 가정합니다. 이 알파 레벨에 해당하는 z-임계 값은 무엇입니까?

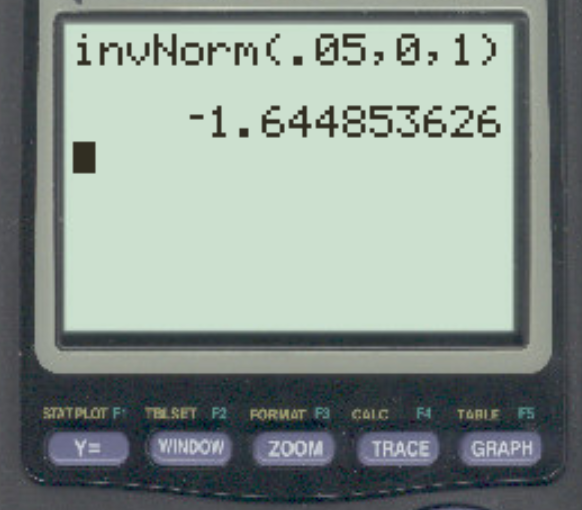
답은 z = -1.64485 입니다.

연구자가 α = 0.05를 사용하여 직선 가설 검정을 수행한다고 가정합니다. 이 알파 레벨에 해당하는 z-임계 값은 무엇입니까?

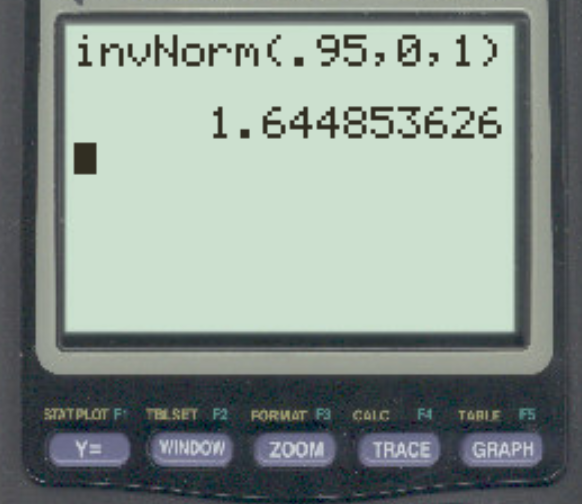
답은 z = 1.64485 입니다.

예 2: 양면 테스트의 임계 Z 값

연구자가 α = 0.05를 사용하여 양측 가설 검정을 수행한다고 가정합니다. 이 알파 레벨에 해당하는 z-임계 값은 무엇입니까?

이 임계값을 찾기 위해 공식 1 – α/2를 사용할 수 있습니다. 이 경우 확률로 1 – 0.05/2 = 0.975를 사용합니다.

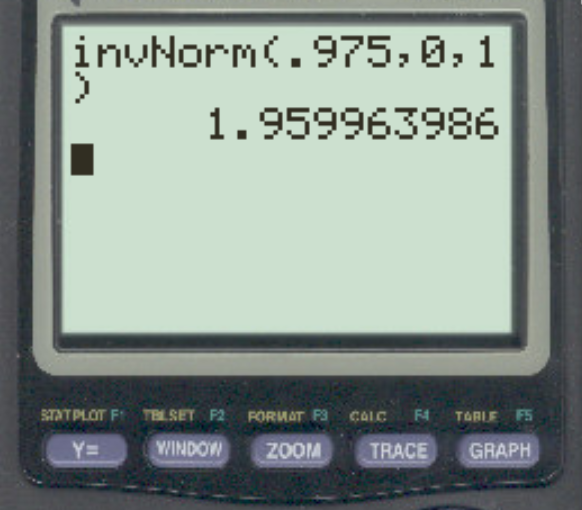
답은 z = 1.96 입니다.

예 3: 컷오프 점수에 대한 임계 Z 값

특정 시험의 점수가 평균 70, 표준편차 8의 정규 분포를 따른다고 가정해 보겠습니다. 상위 10%를 나머지 점수와 구분하는 점수는 무엇입니까?

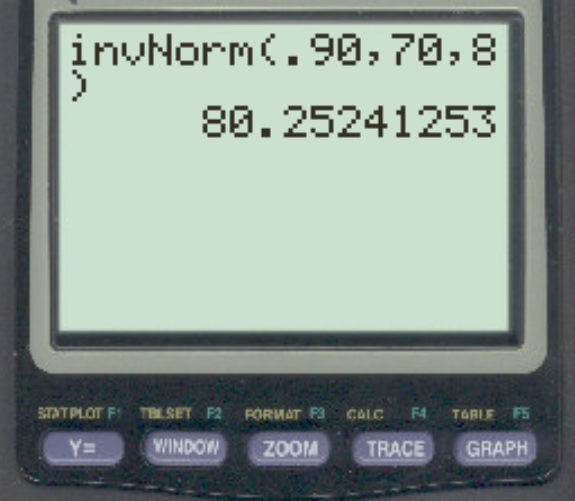
답은 80.25 입니다.

특정 도시에 거주하는 남성의 키가 평균 68인치, 표준편차 4인치로 정규 분포를 따른다고 가정해 보겠습니다. 하위 25%가 나머지와 얼마나 높은 차이를 보이나요?

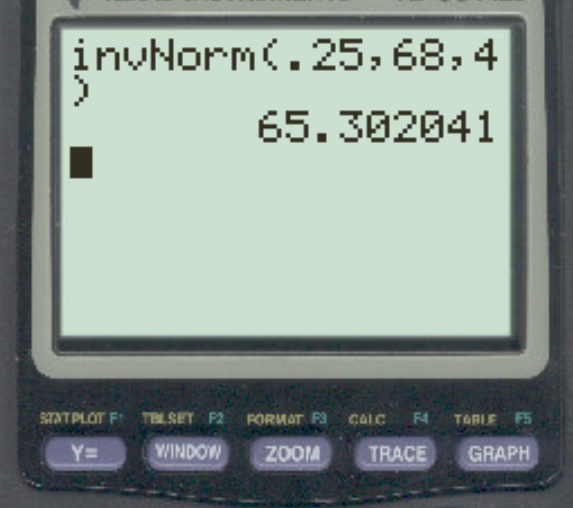
답은 65.3 인치이다.

추가 리소스

TI-84 계산기에서 이항 확률을 계산하는 방법
TI-84 계산기에서 포아송 확률을 계산하는 방법
TI-84 계산기에서 기하학적 확률을 계산하는 방법