Excel에서 중심 극한 정리를 적용하는 방법
중심 극한 정리 는 모집단 분포가 정규 분포가 아니더라도 표본 크기가 충분히 크면 표본 평균의 표본 분포가 대략 정규 분포를 따른다는 것 입니다.
중심 극한 정리는 또한 샘플링 분포가 다음과 같은 속성을 갖는다고 명시합니다.
1. 표본분포의 평균은 모집단 분포의 평균과 같습니다.
x = μ
2. 표본분포의 표준편차는 모집단 표준편차를 표본 크기로 나눈 값과 같습니다.
s = σ / √n
이 튜토리얼에서는 Excel의 중심 극한 정리를 주어진 분포에 적용하는 방법을 설명합니다.
Excel에서 중심 극한 정리 적용
평균이 8 이고 표준편차가 4 인 분포가 있다고 가정합니다. Excel에서 다음 수식을 사용하여 표본 크기가 15 인 표본 분포의 평균과 표준 편차를 모두 찾을 수 있습니다.
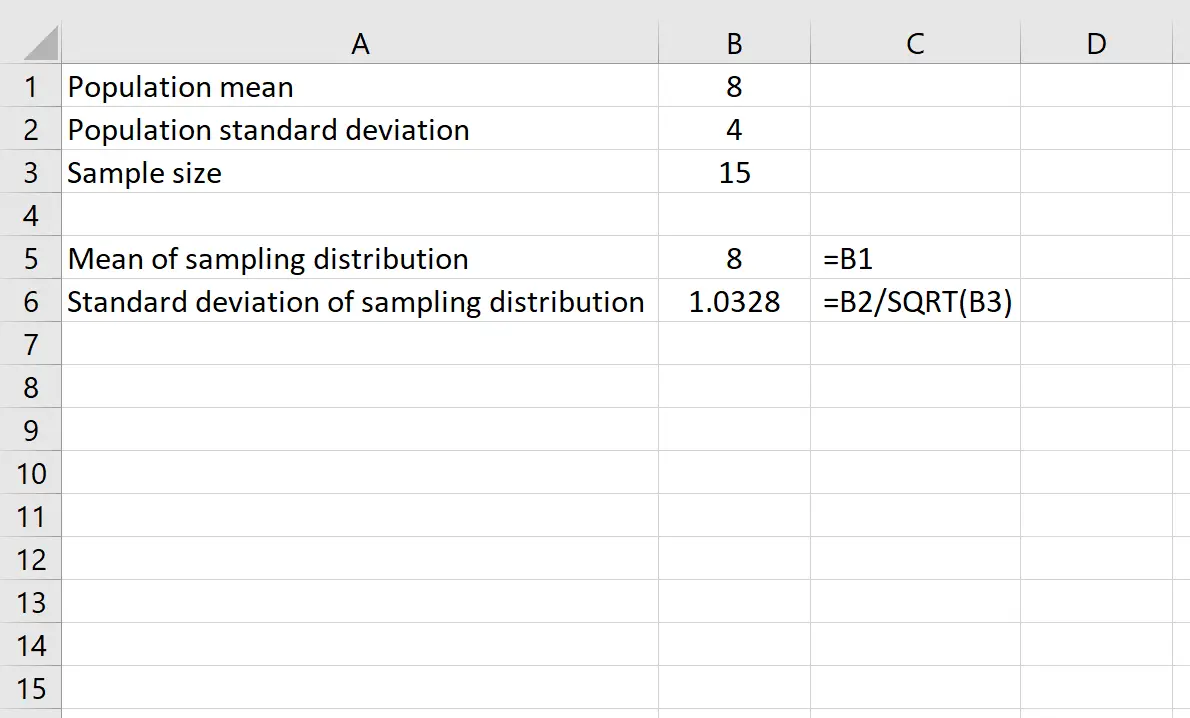
표본분포의 평균은 모집단 분포의 평균인 8 과 같습니다.
표본분포의 표준편차는 모집단 표준편차를 표본 크기로 나눈 것과 같습니다. 즉, 4 /√15 = 1.0328 입니다 .
확률에 관한 질문에 대답하기 위해 중심 극한 정리를 사용할 수도 있습니다. 예를 들어, 주어진 모집단의 평균이 8 이고 표준 편차가 4 라면 주어진 크기 15 의 표본이 나올 확률은 얼마입니까? 평균이 7 이하입니까?
이 질문에 답하기 위해 Excel에서 다음 구문을 사용하는 NORM.DIST() 함수를 사용할 수 있습니다.
NORM.DIST(x, 평균, 표준_개발, 누적)
금:
- x: 샘플은 테스트하고 싶다는 의미입니다.
- 평균: 표본 추출 분포의 예상 평균
- Standard_dev: 샘플링 분포의 예상 표준 편차
- 누적: TRUE는 일반 CDF 값을 반환합니다. FALSE는 일반 PDF 값을 반환합니다. 우리의 경우에는 항상 TRUE를 사용합니다.
이 함수는 표본 평균이 특정 값보다 작거나 같을 확률을 반환합니다.
이 예에서 사용할 수식은 다음과 같습니다.
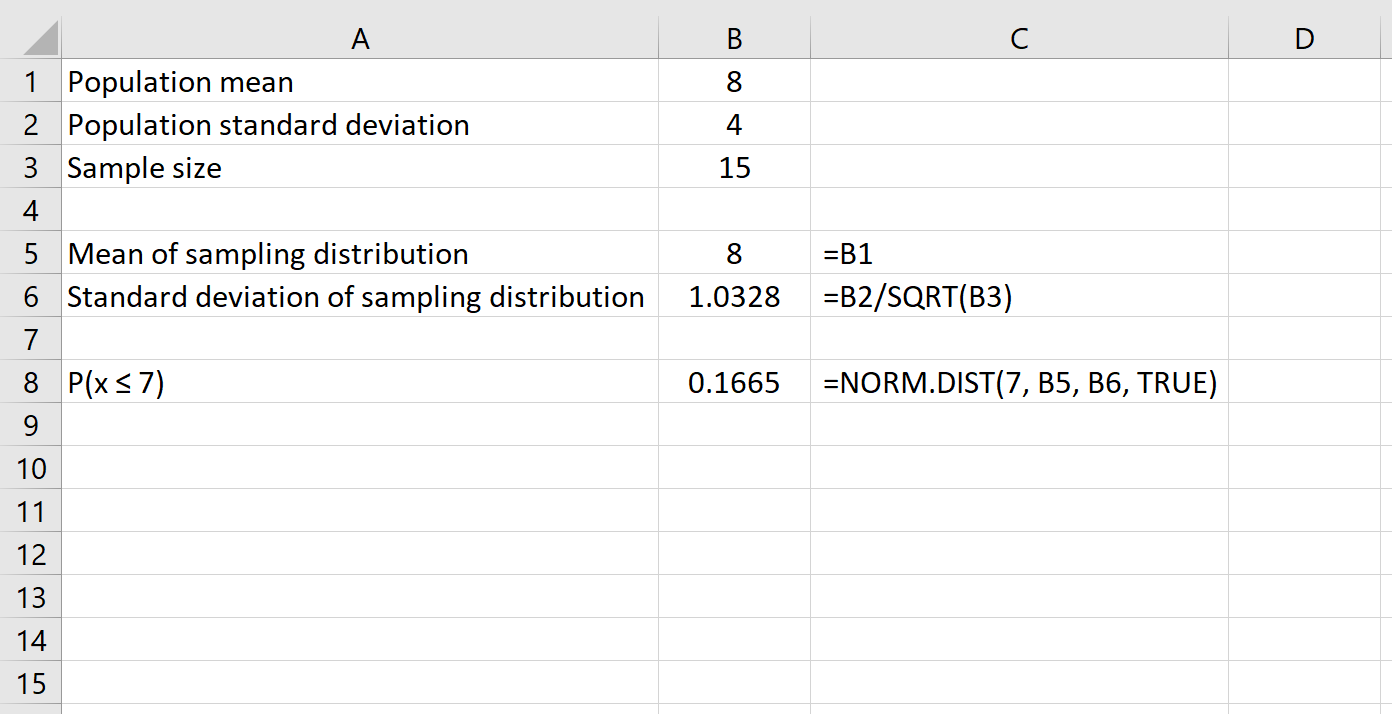
이는 평균이 8 이고 표준 편차가 4 인 모집단의 경우 주어진 크기 15 의 표본이 평균은 7 또는 0.1665 보다 작거나 같습니다.
또한 공식 1 – NORM.DIST()를 사용하여 주어진 표본 크기가 특정 숫자보다 큰 평균을 가질 확률을 찾을 수도 있습니다.
예를 들어, 다음 공식은 주어진 표본 크기 15에서 평균이 7 보다 큰 확률을 결정하는 방법을 보여줍니다.
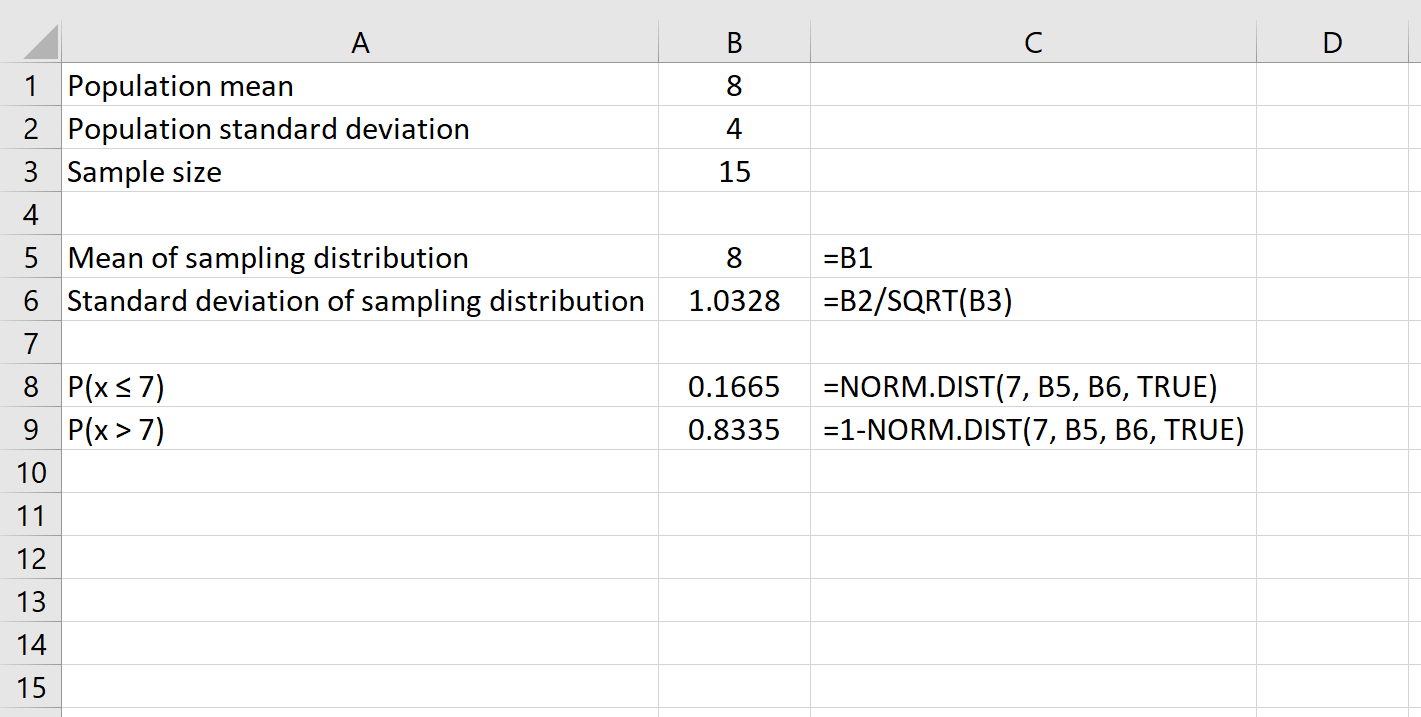
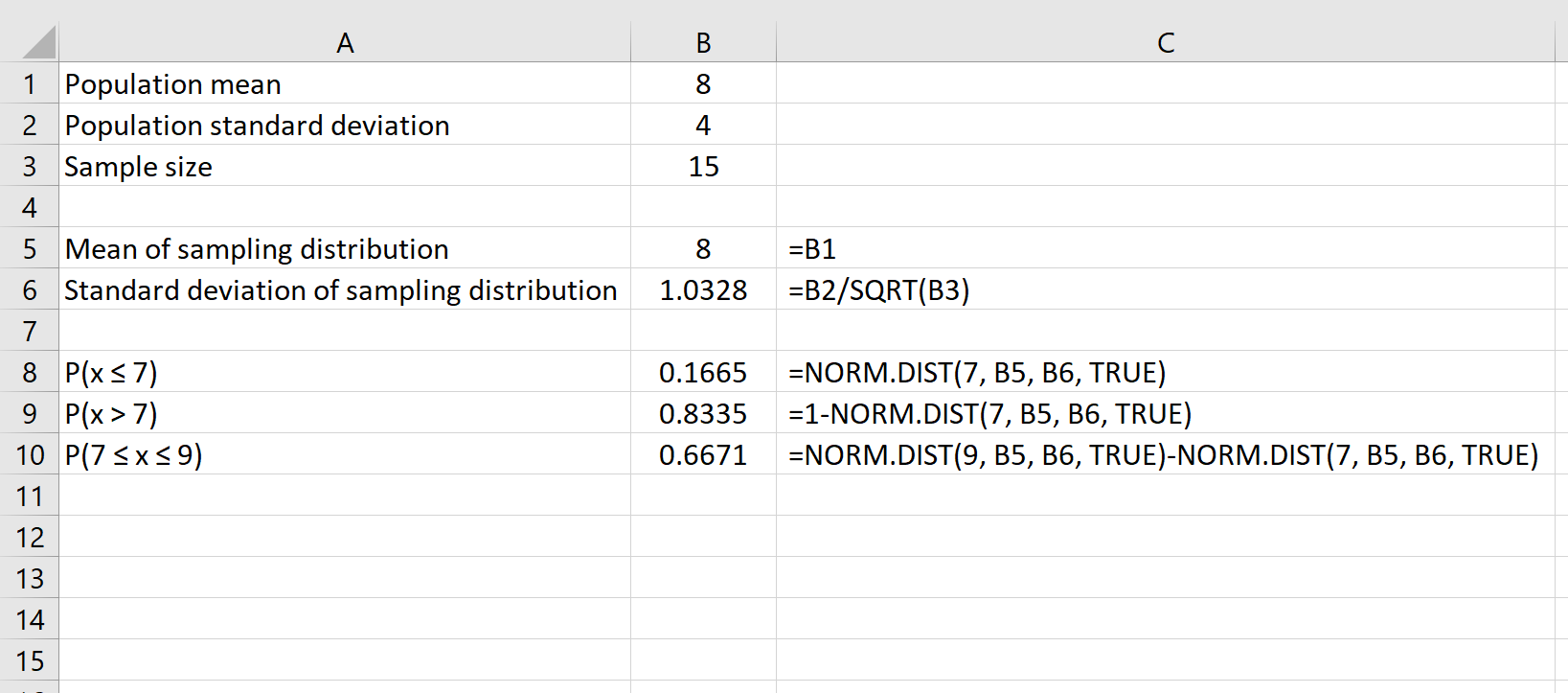
마지막으로, NORM.DIST(큰 숫자) – NORM.DIST(작은 숫자) 공식을 사용하여 주어진 표본 크기가 두 숫자 사이의 평균을 가질 확률을 찾을 수 있습니다.
예를 들어, 다음 공식은 주어진 표본 크기 15에서 평균이 7과 9 사이일 확률을 찾는 방법을 보여줍니다.